反作用輪鉸間隙對航天器動態特性影響分析

潘 冬，趙 陽，王興貴，馬文來

(哈爾濱工業大學 航天學院，哈爾濱 150001)

反作用輪是高精度航天器姿態控制的主要擾動源之一，隨著航天事業的發展及哈勃望遠鏡、新一代望遠鏡(NGST)等一系列航天器的發射升空，預示著未來的航天器向高精度、高穩定性方向發展，目前中國在軌飛行的中低軌道遙感衛星成像精度與國際先進水平有明顯差距，其主因即為飛輪擾動所致，對此迫切需要深入研究。

早在20世紀70年代，美國為解決反作用輪高頻振動對哈勃望遠鏡成像精度的影響，對其使用的反作用輪擾動特性進行了深入研究。王全武［1］等提出了一種基于經驗的飛輪擾動模型。Bialke［2］對反作用輪擾動的來源、實驗與數學建模進行了全面的闡述。目前我國對飛輪擾動問題開展的研究集中在飛輪擾動理論模型建模技術主要考慮飛輪轉子不平衡(靜不平衡、動不平衡)、飛輪結構撓性、軸承振動與摩擦特性以及電機輸出轉矩特性等四方面［3－7］。未考慮飛輪轉子與軸承間鉸間隙的影響，運動副的存在間隙不可避免，運動副間隙主要由兩種因素造成，一種由設計動配合生產加工形成的規則的原始裝配間隙，一種由磨損引起的非規則的附加間隙，由于轉子不平衡在旋轉中發生偏心，且存在間隙，轉子與軸套間發生接觸碰撞產生的沖擊，嚴重影響航天器的控制精度與穩定性。

本文以某高指向要求的遙感觀測衛星為例，基于虛擬樣機技術，引入間隙矢量模型，對鉸間隙進行建模，通過對Adams中已有模型參數的設定及自定義模型的引入，得到考慮飛輪鉸間隙的衛星系統虛擬樣機模型，分析其反作用輪鉸間隙對衛星系統動態特性的影響，進而為控制系統的設計與優化提供參考。

1 反作用輪間隙鉸動力學建模

反作用輪是衛星姿控系統關鍵執行部件，主要由支撐軸、軸承、飛輪轉子、驅動電機等零部件組成［8］，驅動電機輸出力矩使飛輪轉子高速旋轉，從而提供衛星進行姿態機動或保持的力矩。飛輪轉子與軸承間存在間隙，由于飛輪轉子的動不平衡，轉子與軸承間發生接觸碰撞，隨著運行時間的變長將產生磨損，加大間隙，間隙的變大又會導致碰撞沖擊劇烈進一步磨損，這是個循環促進的過程，研究鉸間隙對機構動態特性影響，其關鍵是對鉸間隙進行正確描述。

1.1 間隙鉸矢量模型

運動副鉸間間隙的存在對機構主要有兩方面的影響:首先，由于間隙的存在，系統成為拓撲結構可變的系統。含間隙的系統具有兩種拓撲結構:一種是兩體之間在間隙的方向上失去鉸間約束，構件體做自由運動;另一種是兩體之間相互接觸，構件體做具有單邊約束的運動。間隙的另一個影響是機構在運動中產生內碰撞，含間隙的變結構系統總是在自由運動和單邊約束兩種狀態間相互切換，而這種狀態間的切換幾乎不可能是光滑、平穩的，總要包含一定的碰撞，而碰撞即會產生碰撞力，從而影響機構的穩定性。

對衛星反作用輪系統鉸間隙的真實有效描述是實現衛星系統運動、動力學仿真的關鍵。本文主要定性研究反作用輪鉸間隙對衛星系統的影響，將軸承考慮成軸套，不考慮軸承的復雜結構。如圖1所示，間隙矢量模型通過在轉子軸和軸套的旋轉鉸中引入一個間隙矢量來表達旋轉鉸的真實潛在行為，間隙矢量表征軸和軸套兩構件間連接點的精確相對位置。

間隙矢量定義在一個局部浮動笛卡爾坐標系中，以軸套的回轉中心為間隙矢量的基準起始點，間隙矢量的方向指向軸和軸套相對運動時的潛在接觸點，該潛在接觸點構成了軸與軸套的相對碰撞點對。間隙矢量的大小被嚴格限制在以軸套回轉中心為圓心且以軸和軸套的徑向尺寸公差為半徑的間隙圓內，間隙矢量大小的變化能反映間隙運動副元素是否接觸［9］。

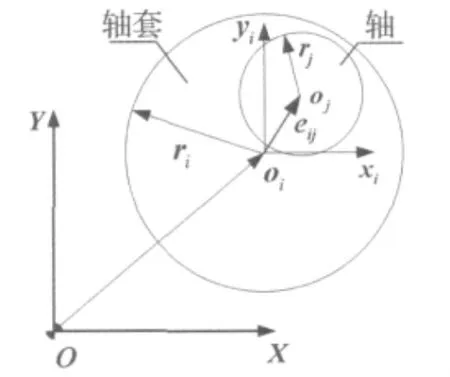
圖1 運動副間隙矢量模型Fig.1 Sketch of revolute joints with clearance

對含間隙反作用輪系統，假設轉動副鉸接處軸套與軸同心，間隙大小用軸套與軸半徑之差表示，則間隙為:

式中:ri為軸套半徑，rj為轉子軸半徑，eij為間隙矢量。

1.2 間隙鉸數學模型

圖2為軸與軸套碰撞時旋轉鉸間隙示意圖，Oi和Oj分別為軸承和軸的中心和是軸套和軸的中心在全局慣性坐標系下位置矢量。

由圖2可知，軸套與軸的間隙矢量為:

根據間隙矢量定義知，間隙矢量表示軸相對于軸套的偏心矢量。軸與軸套碰撞時的法線單位矢量表示為:

Qi和Qj分別為軸套和軸的潛在接觸點，和是軸套和軸潛在接觸點對在全局慣性坐標系下的位置矢量，當軸套和軸接觸碰撞時，碰撞引起接觸變形的大小表示為:

其中:c為初始間隙，是軸套與軸的半徑之差，由式(1)求得。因此接觸變形量與間隙矢量相關。

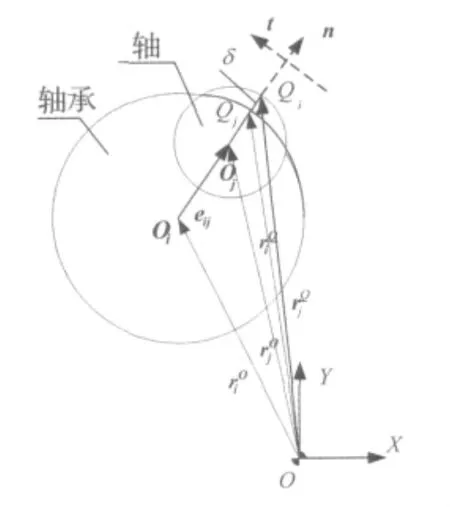
圖2 碰撞時旋轉鉸間隙示意圖Fig.2 Bump of revolute joints with clearance

軸與軸套是否發生碰撞可根據接觸變形量δ判定，軸與軸套接觸碰撞條件為:

在軸與軸套發生接觸碰撞時，會產生接觸碰撞力，為計算碰撞力大小，需知道軸與軸套碰撞時接觸面間法向相對速度及切向相對速度，將δ·向碰撞接觸平面投影即可得到:

法向單位矢量n的方向可根據式(3)求得，切向單位矢量t的方向可由n逆時針旋轉90°得到。

1.3 間隙鉸接觸碰撞力模型

間隙鉸的一個重要特征就是其系統為變拓撲系統，即分為無約束的自由運動和受單邊幾何約束的運動，自由運動時機構在運動副處不受力的作用較好處理，但是當受單邊幾何約束時，運動副處將會有力的作用，為了建立系統動力學模型，需要將幾何約束轉化為力約束，利用合理的碰撞力模型來預測接觸碰撞力將是建立正確動力學模型的關鍵。

本文采用非線性彈簧阻尼模型建立軸與軸套間隙接觸碰撞模型［10－11］，如圖3所示其廣義形式表示為:

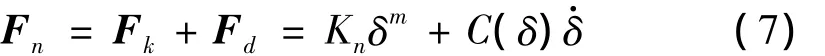
式中:Fn為接觸點法向接觸力;Kn為等效接觸剛度;δ為接觸點法向穿透深度為接觸點法向相對速度;C(δ)為與δ有關的阻尼因子;m為指數，m≥1。彈簧恢復力Fk由Hertz接觸理論確定:

為克服線性阻尼模型接觸初始時刻碰撞力不為零的局限性，采用非線性阻尼模型確定接觸碰撞過程中的阻尼力Fd:

其中:C為阻尼系數，與恢復系數及接觸剛度有關:

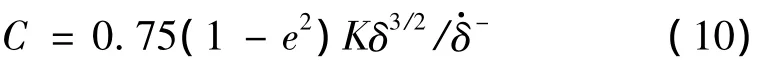
等效接觸剛度Kn取決于兩個接觸碰撞體的幾何特征及材料屬性，根據Hertz接觸理論可知:

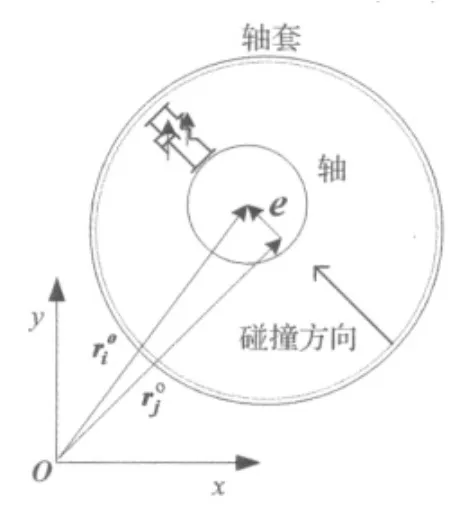
圖3 旋轉鉸非線性彈簧阻尼模型Fig.3 Nonlinear equivalent spring-damp model

其中:ν，E分別為泊松比與楊氏模量。

1.4 間隙鉸摩擦力模型

反作用輪轉子與軸套間還存在切向摩擦力，其力矩會進一步影響含間隙機構的動力學特性，求解間隙處切向摩擦力采用修正的Coulomb摩擦模型［12］，切向摩擦力表示為:

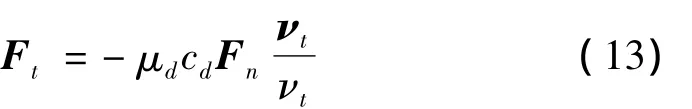
其中:μd為滑動摩擦系數，cd為動態修正系數，νt為相對切向速度。cd由下式獲得:

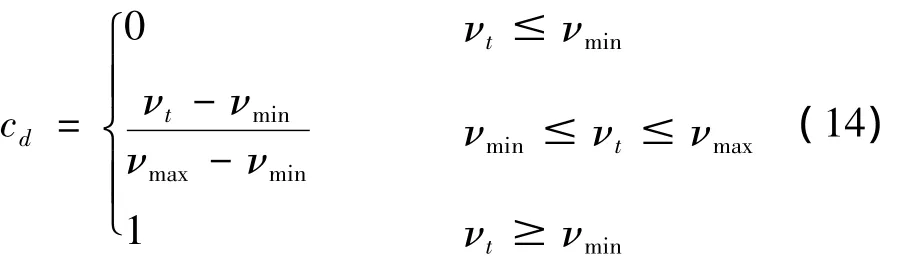
式中:νmin，νmax為給定的速度極限值。

通過建立的法向接觸力與切向摩擦力模型，可較準確描述反作用輪系統間隙鉸處的約束問題，從而根據多體動力學理論得到考慮反作用輪鉸間隙的衛星系統動力學方程。

引入階躍函數:

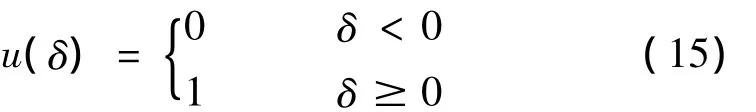
間隙處約束力為:

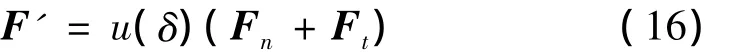
從而含間隙雙軸驅動機構動力學方程為:

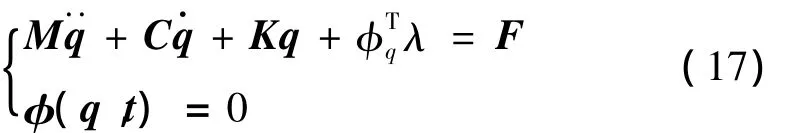
式中:q為廣義坐標列陣，M，C，K，φq，F分別為衛星系統的廣義質量陣、阻尼陣、剛度陣、約束方程的雅克比矩陣、廣義速度二次項以及力陣的和，λ為Lagrange乘子列陣。

2 虛擬樣機模型

對于含間隙機構動力學問題，準確檢測接觸碰撞點并精確求解是研究的難點問題。當建立了機構的動力學模型后，如何編程實現對接觸碰撞點的實時檢測將很困難，而多體動力學分析軟件Adams能很好的解決這一問題，所以本文基于虛擬樣機技術，應用Adams計算平臺對考慮反作用輪鉸間隙的衛星系統進行仿真分析。

衛星的整星結構包括推進艙、服務艙、有效載荷艙以及太陽帆板、連接架、服務艙隔板等。其中在服務艙中裝有反作用輪系統，本文主要研究反作用輪轉子與軸套間隙對衛星系統動態特性的影響，所以在太陽帆板、連接架等結構與衛星本體間定義固定副，作為一個整體，不計太陽帆板柔性的影響。為考慮飛輪轉子不平衡因素的影響，在轉子上加一較小的附加質量，如圖4所示。

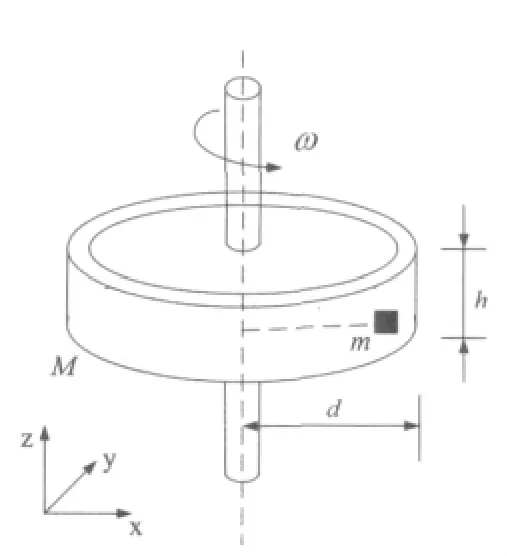
圖4 反作用輪不平衡示意圖Fig.4 Reaction wheel unbalanced

通過建立的反作用輪間隙處動力學模型，用間隙鉸處接觸碰撞產生的力約束代替含間隙的幾何約束，從而達到考慮鉸間隙進行動力學仿真的目的，圖5為建立的衛星系統虛擬樣機模型。

圖5 衛星系統虛擬樣機Fig.5 Virtual prototype model of satellite

3 仿真結果與分析

間隙鉸的存在，對衛星系統的動態特性及指向精度都將產生一定的影響，基于建立的虛擬樣機，分別針對飛輪轉子與軸套間為理想鉸及間隙鉸兩種情況進行仿真分析，分析鉸間隙對各特征變量的影響。

3.1 仿真條件

航天器材料為鋁蜂窩夾層板結構，在進行仿真運算時，對其結構特性進行假設等效，仿真中的結構參數如表1所示。反作用輪轉子半徑rj=0.0195 m，軸套半徑為ri=0.02 m。半徑間隙c=0.0005 m，電機輸出力矩為M1=0.1 Nm，間隙接觸等效剛度值為1.3×108N/m、等效阻尼值為176 Ns/m，滑動摩擦系數為0.1。

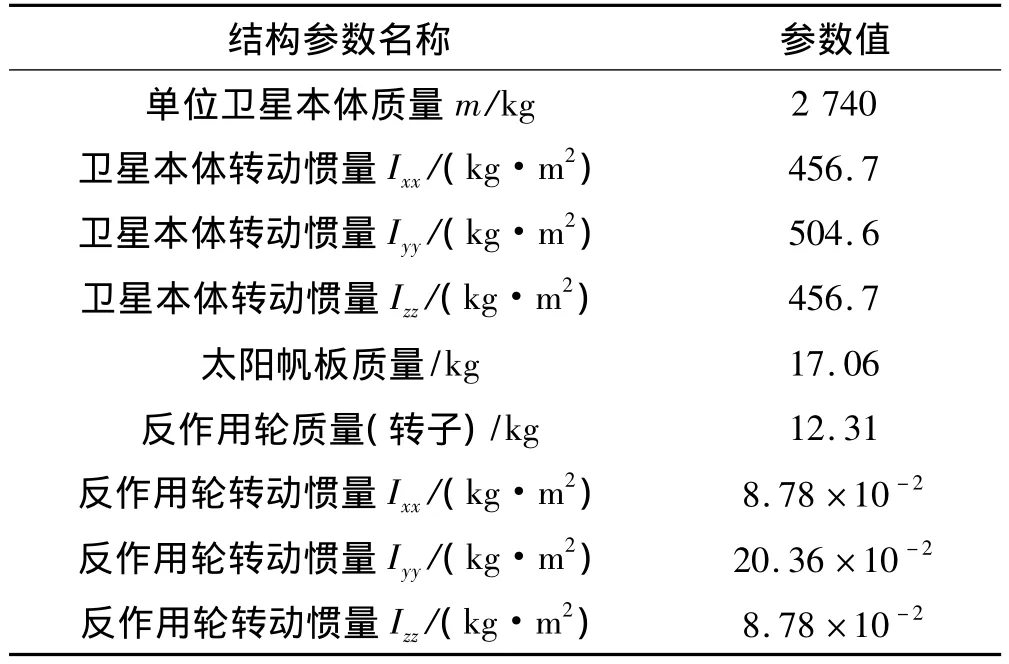
表1 衛星系統結構參數Tab.1 Structure parameters of the satellite

3.2 結果分析

根據以上仿真條件，對衛星系統虛擬樣機進行仿真分析，結果如圖6所示。

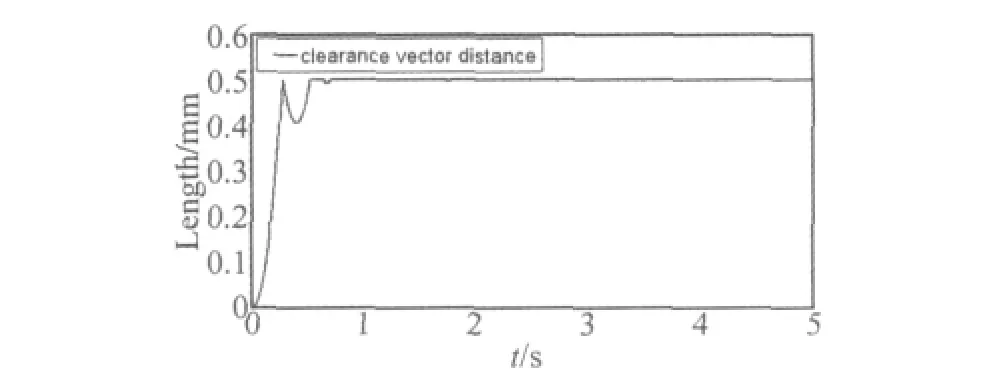
圖6 間隙矢量距Fig.6 Sketch of revolute joints with clearance

圖6為反作用輪轉子與軸套的間隙矢量距，根據間隙矢量定義知，初始時轉子與軸套同心，間隙矢量距為0，當電機對轉子施加轉矩后，轉子轉動并發生偏心，與軸套接觸碰撞，軸套與轉子間隙為0.5mm，當間隙矢量距達到0.5mm時即代表發生接觸，從圖中可看出只是在運動初期轉子與軸套有脫離接觸，隨著轉子轉速的增加，兩者一直保持接觸狀態，即運動副間發生連續接觸變形。

圖7 衛星系統平動特性Fig.7 Translational characteristics of satellite systems

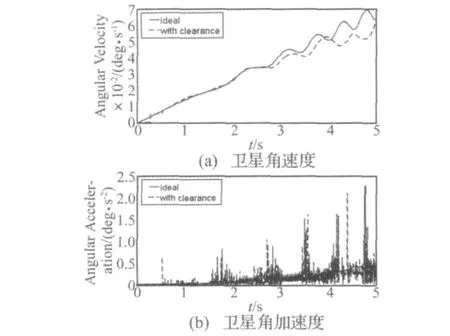
圖8 衛星系統轉動特性Fig.8 Rotational characteristics of satellite systems

圖7為衛星本體在反作用輪作用下，理想鉸與間隙鉸兩種不同工況下質心的平動特性，其中圖7(a)為質心的位移曲線，由于間隙的存在，使衛星在姿態機動過程中位置出現偏差，且隨著時間的積累偏差逐漸增大。從圖7(b)、圖8(a)衛星的平動速度、角速度曲線中看出，間隙使衛星速度發生波動，而間隙處消耗能量，在電機輸出轉矩相同情況下，考慮間隙時衛星的機動速度小于理想情況下的速度。圖7(c)、圖8(b)衛星的加速度曲線表明，間隙使間隙鉸處發生內碰撞，加速度出現很大的峰值。

通過分析可知，由于反作用輪轉子與軸套間存在的間隙，使衛星系統的速度與加速度都出現很大的波動，對于系統的穩定性及定位精度極其不利。

圖9為衛星反作用輪系統間隙鉸處產生的接觸碰撞力，其中圖9(a)、圖9(b)分別為法向接觸力和切向摩擦力，由動力學建模過程可知，法向接觸力由彈簧阻尼器等效求得，而摩擦力則根據修正的庫倫摩擦力模型求得。從圖中可看出，由于間隙的存在，間隙鉸處發生內碰撞，法向力和摩擦力都有很大的沖擊峰值，且法向力數值大于摩擦力，圖9(c)為接觸碰撞力的合力與理想鉸鉸間力的對比，從圖中明顯看出考慮間隙情況下的接觸碰撞力遠大于理想情況下產生的鉸間力，最大峰值約為理想情況下的10倍，過大的沖擊力將加速機構的破壞與磨損，反作用輪鉸間隙的存在對于衛星系統的定位精度及工作壽命影響極大。

圖9 間隙接觸碰撞力Fig.9 Joint clearance bump force

4 結論

反作用輪作為衛星姿態控制系統的關鍵執行部件，其也是影響高精度航天器的主要擾動源之一，文中采用非線性彈簧阻尼模型建立了間隙處的接觸碰撞模型，同時采用修正的Coulomb摩擦模型考慮運動副間隙處的摩擦作用，研究了反作用輪鉸間間隙對衛星系統動態特性的影響。仿真結果表明:

(1)反作用輪鉸間隙的存在，將影響衛星系統的定位精度，出現定位偏差，且隨著運行時間的增長，偏差累積增大。

(2)間隙的存在使鉸間發生內碰撞，引起衛星系統速度、加速度劇烈抖動，產生很大的峰值。

(3)鉸間的內碰撞將產生很大的接觸碰撞力，加速機構的磨損與破壞，影響反作用輪系統的使用壽命。運動副間隙不可避免，在建立反作用輪系統擾動模型時應充分考慮間隙對系統的影響，以獲得更準確的擾動模型，為航天器材料的選擇及控制系統設計提供參考。

［1］王全武，虎 剛.飛輪擾動原因與測量技術現狀［J］.空間科學學報，2009，29(1):39 －44.

［2］Bialke B.A compilation of reaction wheel induced spacecraft disturbances［C］.Proceedings of the 20th Annual AAS Guidance and Control Conference，AAS，1997:97 －038.

［3］孫 杰，趙 陽，王本利.航天器反作用輪擾動精細模型［J］.哈爾濱工業大學學報，2006，38(4):520 －522.

［4］張鵬飛，程 偉，王 和.航天器反作用輪擾動建模及參數辨識［J］.北京航空航天大學學報，2010，36(7):879－882.

［5］李連軍，戴金海.反作用輪系統內干擾建模與仿真分析［J］.系統仿真學報，2005，17(8):1855 －1863.

［6］龐世偉，楊 雷，曲廣吉.高精度航天器微震動建模與評估技術最近進展［J］.強度與環境，2007，34(6):1 －9.

［7］孫 杰，趙 陽，田 浩.改善航天器反作用輪擾動實驗模型參數辨識方法［J］.空間科學學報，2006，26(1):70－74.

［8］白爭鋒，趙 陽，馬文來.反作用輪擾動對航天器結構動態特性的影響分析［J］.宇航學報，2009，30(5):2073－2079.

［9］時 兵，金 燁.面向虛擬樣機的機構間隙旋轉鉸建模與動力學仿真［J］.機械工程學報，2009，45(4):299 －303.

［10］Dubowsky S， Freudenstein F. Dynamic Analysis of Mechanical Systems with Clearances，Part 2:Dynamic Response［J］.Trans.ASME.Eng.Ind.，1971，93(1):310－316.

［11］Flores P.Dynamic analysis of mechanical systems with imperfect kinematic joints［J］.Universidade Do Minho PhD thesis，2004:50 －62.

［12］Flores P J.Modeling and simulation of wear in revolute clearance joints in multibody systems［J］.Mechanism and Machine Theory，2009，44:1211－1222.