歐氏空間的等積變換的性質

王朝霞，張 慶

（唐山師范學院 數學與信息科學系，河北 唐山 063000）

數學研究

歐氏空間的等積變換的性質

王朝霞，張 慶

（唐山師范學院 數學與信息科學系，河北 唐山 063000）

首先給出了歐氏空間的等積變換的定義。其次給出4個引理并利用這些引理給出了有限維歐氏空間的兩個線性變換為等積變換的充要條件，其中一個充要條件反應了兩個等積變換在規范正交基下的矩陣關系，另一個充要條件反應了兩個等積變換之間的關系。最后給出了無限維歐氏空間為等積變換的一個充要條件及等積變換的一個性質。

歐氏空間；線性變換；等積變換；規范正交基

1 引言

在歐氏空間V中，若,σ τ 為V的兩個正交變換，則對任意的ξ, η∈V，都有

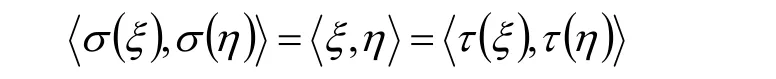
反之，如果對任意的ξ, η∈V，都有

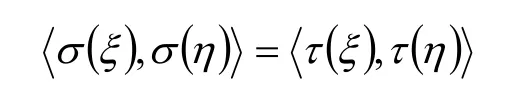
那么,σ τ 未必是為V的兩個正交變換。本文要研究保持內積不變的同一歐氏空間的兩個線性變換的關系。

2 預備知識

定義 在歐氏空間V中，,σ τ 為V的兩個線性變換，若對任意的ξ, η∈V都有

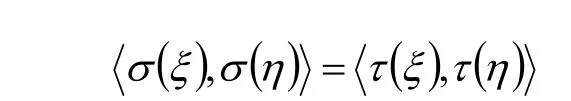
則稱,σ τ 為V的兩個等積變換。

引理1[1]若V是歐氏空間，V的向量組

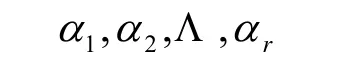
線性無關的充要條件是及

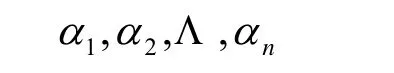
引理2 若V是歐氏空間，V的兩個向量組為由X, Y的任意性知ATA=BTB=0，即ATA=BTB。

由引理及定理1可得定理2。

定理2 若σ,τ為n維歐氏空間V的兩個線性變換，則σ,τ為V等積變換的充要條件是存在正交變換φ，使得φσ=τ。

證明 充分性。若存在正交變換φ，使得σ=φτ，則對任意的ξ,η∈V，都有

σ（ ξ）,σ（ η）=φ（ τ（ ξ））, φ（ τ（ η））=τ（ ξ）,τ（ η）

因此σ,τ為V的兩個等積變換。

必要性。若σ,τ為V的兩個等積變換，設

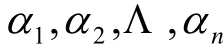
為歐氏空間V的一個規范正交基，σ,τ關于

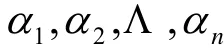
的矩陣分別為A,B，由定理1，ATA=BTB，而ATA的位于第i行第j列的元素為

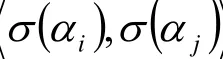
而BTB的位于第i行第j列的元素為

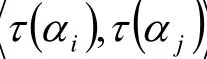
從而

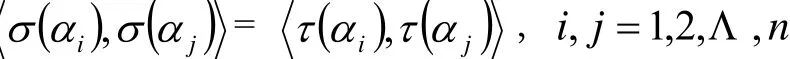
由引理4，存在V的正交變換φ使得

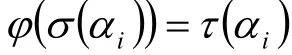
即

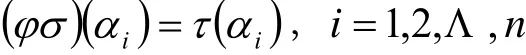
又α1,α2,Λ,αn為歐氏空間V的一個規范正交基，于是φσ=τ。

推論1 設矩陣A,B為n階實矩陣，則ATA=BTB的充要條件是存在n階正交矩陣U，使得B=UA。

證明：若σ, τ為n維歐氏空間V的兩個線性變換，并且σ, τ關于V的規范正交基α1,α2,Λ,αn的矩陣分別為A,B。由定理1知，ATA=BTB的充要條件σ,τ為V的等積變換，由定理2知σ, τ為V的等積變換的充要條件是存在正交變換φ，使得φσ=τ，設并且正交變換φ關于V的規范正交基α1,α2,Λ,αn的正交矩陣為U，則B=UA。

2.2 無限維歐氏空間的兩個線性變換為等積變換的性質

當歐氏空間V不是有限維歐氏空間時，在討論等積變換時，不能利用規范正交基及矩陣這樣的工具，在某些條件下有以下定理。

定理3 若σ, τ為歐氏空間V的兩個線性變換，且σ或τ為可逆變換，則σ, τ為V等積變換的充要條件是存在正交變換φ，使得φσ=τ。

證明 充分性的證明與定理2相同。

必要性：若σ, τ為V的兩個等積變換，不妨設σ為可逆變換。對任意的ξ,η∈V，設

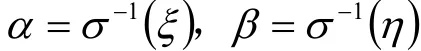
則α，β∈V。由于σ, τ為V的兩個等積變換，則

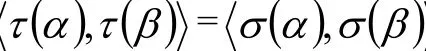
即

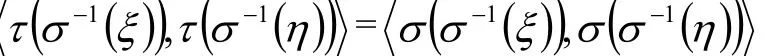
所以

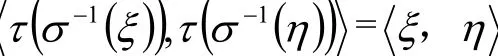
所以，τσ-1為正交變換，令φ=τσ-1，則τ=φσ，其中φ為正交變換。

定理4 若σ,τ為歐氏空間V的兩個等積變換，則σ（V ）與τ（V ）同構。

證明 對任意ξ∈V，令φ: σ（ ξ）→τ（ ξ），則φ是σ（V）到τ（V）的映射，且為滿射。對任意ξ, η∈V，若

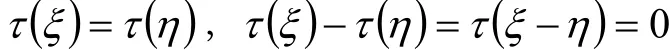
由于σ, τ為V的兩個等積變換，則

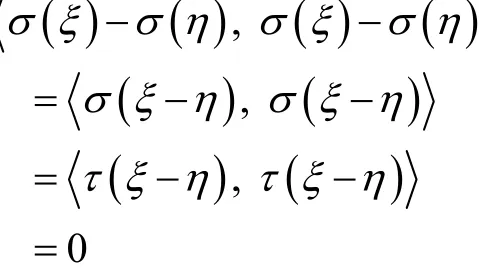
所以，σ（ξ）=σ（η），即φ是σ（V ）到τ（V）的單射。對任意的ξ, η∈V及任意實數k, l，

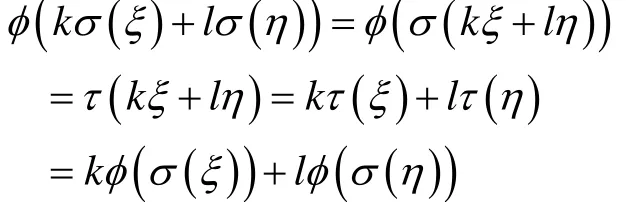
對任意的ξ, η∈V，

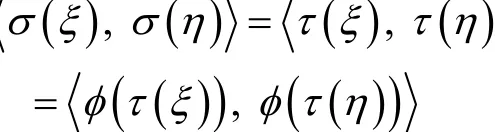
因此，φ是σ(V)到τ(V)的同構映射，亦即σ(V)與τ(V)同構。

[1]王品超.高等代數新方法[M].濟南:山東教育出版社, 1989:462-463.

[2]張禾瑞,郝鈵新.高等代數(第5版)[M].北京:高等教育出版社,2007:302.

[3]白述偉.高等代數選講[M].哈爾濱:黑龍江教育出版社, 1996:312.

（責任編輯、校對：趙光峰）

Properties of the Equi-Inner Product Transformation of Euclidean Space

WANG Zhao-xia, ZHANG Qing
(Department of Mathematics and Information Science, Tangshan Teachers College, Tangshan 063000, China)

This Paper introduces the definition of the equi-inner transformation of Euclidean space. Then gives four lemmas and two necessary and sufficient conditions of what the linear transformation is the equi-inner transformation. One of the necessary and sufficient conditions hint the matrix relations between the two equi-inner transformation matrices under standard orthogonal basis, the other one hint the relationship between two equi-inner transformations. Finally, the necessary and sufficient condition and a property are derived for infinite dimension Euclidean space is an equi-inner transformation.

euclidean space; linear transformation; equi-inner product transformation; standard orthogonal basis

O151

A

1009-9115(2012)05-0030-04

2012-07-20

王朝霞（1963-），女，河北唐山人，教授，研究方向為代數。