一步法精度影響及適用范圍分析

林四海，陳西強，劉 豐 ，凃道勇

(福建省電力勘測設計院，福建 福州 350003)

電力線路勘測和一般的線路勘測有其自身的特點，線路窄而長，電力線走廊通視條件一般較差，尤其是在山區，且對平面和高程精度要求不一致[1]。由于GPS技術其特有的技術優勢，在電力線路勘測中已得到了廣泛的應用[2]。

GPS測量直接得到的是WGS-84系統下的大地坐標及大地高，而工程應用中所采用的一般為1954北京坐標系或西安80坐標系下的坐標，且高程一般為1985高程系統下的值。這就導致存在兩者之間的轉換關系。LEICA Geo Office Combined一共提供3種方法[3]，即經典三維法、一步法和兩步法。其中一步法是一種簡單的強制擬合的方法，其優點是對點的數量要求不高，可以平面和高程分開處理，其高程誤差不影響平面。不需要相關的投影和橢球信息。適用于小區域以及獨立坐標系統，在小區域幾個點轉換的精度甚至優于經典三維法的轉換精度。但該轉換方法只適用于小的區域，不適合進行外推，在外推時精度損失很快。

針對電力線路其自身的特點，在現實工程應用中，對線路區域內已知點的投影和橢球信息一般比較缺乏，其線路兩邊外控點位數量有限，因此一步法可以得到廣泛應用。本文將從一步法的基本理論出發，對先驗坐標值及高程值的精度對轉換后的坐標影響及其適用范圍從理論上給出詳細的分析，對工程實踐具有一定的理論指導意義。

1 一步法原理

1.1 平面坐標轉換

設i點的1954年北京平面坐標為 ( XiYi)54，其對應的WGS84在橫軸墨卡托投影下的平面坐標位 ( xiyi)84，則其在平面坐標之間存在的轉換關系為[4]：

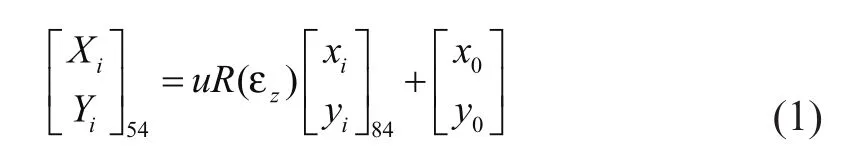
其中：u為尺度比參數， R (εz) 為繞Z軸的旋轉量參數， ( x0y0)T為兩個平面直角坐標系的平移參數，當 εz很小時，有cos εz= 1 ，sin εz=εz，并假設u=1+du，同時去掉二階高次項，則(1)式簡化可表示為：

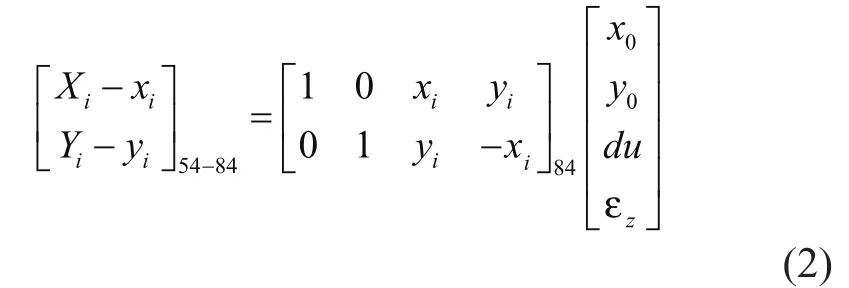
則由(2)式可得誤差方程：

當由n個點參與坐標系配置時，誤差方程可以表示為：

簡記：

并假設其權矩陣為P，根據最小二乘原理可得轉換參數及其相應協因數陣為：

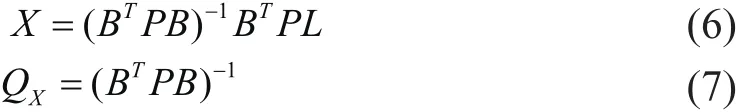
1.2 高程擬合

在高程方面，一步法中高程的解算主要是通過簡單的GPS高程擬合來實現，當公共點位數為0時，不提供高程轉換參數，當只有一個公共點時，即只提供一個插值常數進行強制擬合，這種方法一般精度比較低；當由兩個公共點時，則由兩個高程點推算的平均改正數進行套合，只適合于小區域；當多余2個以上時，通常利用平面擬合進行高程參數的求解，對于平坦或微丘小地區，大地水準面近似看作線性的光滑平面 (變化量約為每10km為0.1m) ，這時可采用最為簡單的一階多項式曲面擬合，即平面擬合[5]。該擬合法需要確定3個參數，因此至少需要知道3個已知點。 它是采用削高補低的原則，平滑出一個曲面來代表擬合區的似大地水準面，供內插和外推使用來求解待定點的正常高。

設測點的高程異常ξ與該點的平面坐標x，y有以下函數關系[6]：

式中： f(x,y)為ξ中的趨勢值， Δ為誤差。設

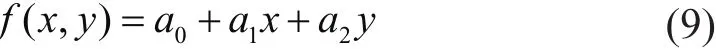
寫成矩陣形式有：

式中：

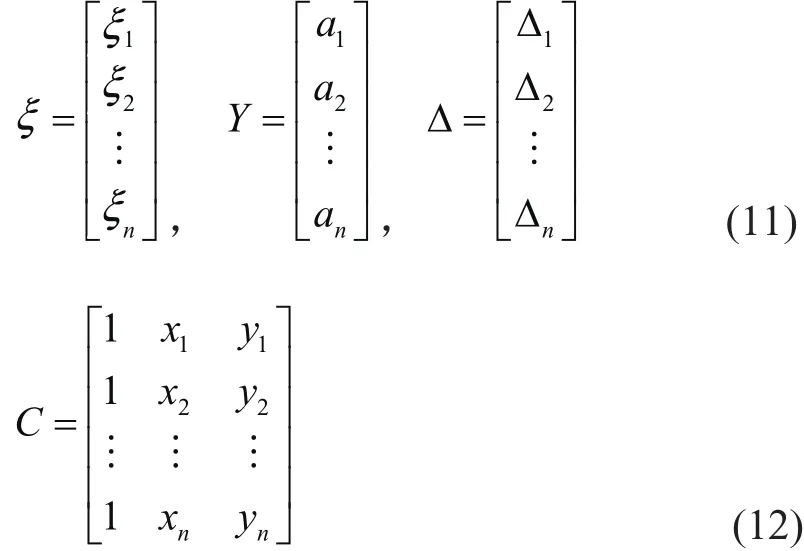
對于每個已知點，都可以列出以上方程，并假設其權矩陣為P，根據最小二乘原理即在∑ ?2=min 的條件下可得擬合參數及其相應協因數陣為：

再按(9)式解出待定點的高程異常值ξ=，從而求出正常高H常。

2 初始值對轉換精度的影響

2.1 初始坐標對平面轉換參數的影響

由前面分析可知，轉換參數的單位權中誤差為：

則由(7)式可知轉換參數的精度為：

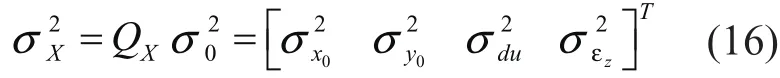
假設1954北京坐標系下的坐標與WGS84坐標系下的坐標是相對獨立的，則由誤差傳播定律[7]可知，轉換參數的精度可用已知坐標的精度來表示為：

由(17)可知參與坐標系配置的已知坐標點精度直接影響到轉換參數的精度，并以近似線性的關系傳遞給轉換后的新坐標值。

2.2 已知高程對高程擬合參數的影響

假設大地高H84和正常高H常是相互獨立的，同理分析可得出擬合參數精度與已知高程點精度的關系為：

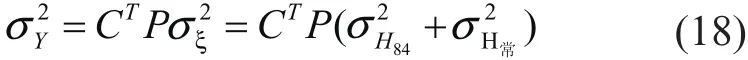
由(18)式可知，已知點高程的大地高及正常高的精度對轉換參數的綜合影響是線性的，并以線性的形式傳遞給最終求解的高程異常值。

需要指出的是，參與高程擬合的已知點與參與平面坐標轉換參數的已知點可以相同，也可以不同。并由以上分析可知，其平面精度與高程精度互不影響。

3 適用范圍分析

3.1 投影平面長度變形分析

一步法這種轉換方法的進行是通過將高程與點位分開進行轉換。在平面點位轉換中，首先將WGS84地心坐標投影到臨時的橫軸墨卡托投影，然后通過平移，旋轉和比例變換使之與計算的“真正的”投影相符合。由此可知其變換的前提是在一個局部的平面格網坐標系中進行轉換，即以水平面代替了具有一定曲率的大地水準面。從而要求點與點之間長度投影變形必須在規范范圍之內或者更嚴格的要求以內。通常投影后對長度的變形影響相對變化見式(19)[8]：

其中：S表示地面上兩點的圓弧長度，R表示地球半徑，ΔS表示投影后長度的變形量，單位均為km。由此可以得出其相對誤差趨勢圖見圖1。

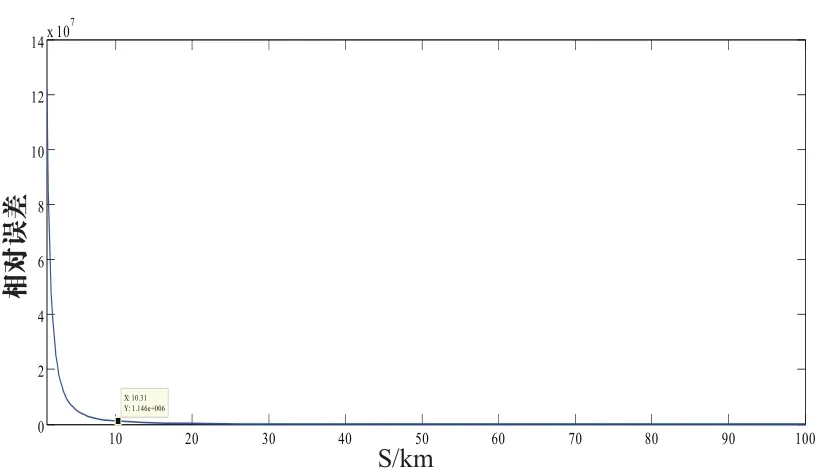
圖1 投影長度變形相對誤差趨勢圖

由圖1可以看出，當在10km以內，其相對誤差在1/1217700以內，而隨著長度的增加，其變形相對誤差相應增大。為滿足以水平面代替了具有一定曲率的大地水準面，一般在10km以內都可以滿足小于1/40000的變形精度要求。

3.2 電臺信號發射半徑分析

考慮RTK作業模式的特點，其中使用一步法時流動站需接受基準站電臺發射出的相位差分改正信息才能得到精確的GPS在WGS84下的大地坐標，進而進行正確的轉換，故信息鏈通訊信號的強度很重要。

由于數據鏈電臺采用高頻載波發送數據，而高頻無線電信號是沿直線傳播的，這就要求參考站發射天線和流動站接收機天線之間理論上無遮擋信號的障礙物。但在現實工程實踐中，往往存在地形、建筑物、無線電信號發射臺之類的影響。一般當電臺信號的發射功率一定時，它的發射距離與基準站電臺天線高度和流動站天線高度以及區域的地形條件存在一定的非線性關系，其中值得參考的是TRIMMRKII電臺的發射半徑D與天線高的關系見式(20)[9-10]：

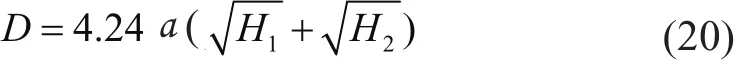
式中：4.24為天寶經驗值，H1電臺的天線高，H2流動站的天線高，a為不同地區的地形條件系數。

當H2=2m時，電臺發射的半徑與基準站電臺天線高及不同地形條件系數的關系如圖2所示。其中a取值為0.1～1.0之間，對于山區地形起伏高差越大，其系數越小。

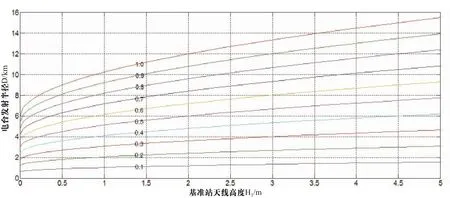
圖2 電臺信號發射半徑與基準站天線高度及地形條件系數的關系

從圖2分析可知，當流動站天線高度一定時，電臺信號發射半徑隨著基準站天線高度的增加而增加，并在0～1m之間電臺信號發射半徑隨著天線高度的增加而增加的速度明顯，1m～5m之間其速度漸趨平緩。同時，不同的地形條件系數對電臺發射半徑的影響存在明顯差異，地形條件越差(對山區來說起伏高差越大)，其發射半徑就限制越大，發射半徑越小。根據福建地形條件及工程實踐經驗，其系數一般在0.2～0.5之間，即當基站電臺天線高度為5m時，其電臺信號發射半徑在3km～8km之間。

4 結論

電力線路勘測具有線路長而窄，電力線路走廊一般通視條件差等顯著特點，其定位模式主要為RTK+全站儀模式。一步法應于電力線路RTK放樣，從理論上對已知點的數量要求不高，可以平面和高程分開處理，其高程精度與平面精度互不影響。同時，參與配置坐標系的已知點平面坐標精度及高程精度對后期測量及放樣點的精度具有近似線性的影響。因此，在實踐工程應用中，對已知點的先驗精度及可靠性必須做一個良好的檢核，其檢核方式一般可以通過對已知點坐標進行復測確定。

對于其適用范圍而言，一步法在理論上可以達到10km的作業半徑，但是受地形條件、電臺發射功率及其天線高度的影響，在福建地區的工程實踐應用中，其作業半徑最大范圍在3km～8km之間。因此可以知道，一步法只能適用于小的區域，當超過最大作業范圍時，必須重新進行配置坐標系。

[1]GB50548-2010，330kV～750kV架空輸電線路勘測規范[S].

[2]黃進航，邱春福.RTGPS在架空送電線路工程測量中的應用[A].2000新技術在工程建設中的應用研討交流會論文集[C].2000.

[3]費應春，牛其志，詹文超.淺談GPS定位成果的坐標轉換[J].中州煤炭，2009，(6).

[4]孔祥元，郭際明，等.大地測量學基礎[M].武漢：武漢大學出版社，2006.

[5]徐紹銓，等.GPS測量原理及應用[M].武漢：武漢大學出版社，2003.

[6]宮雨生.GPS水準模型及其應用研究[D].遼寧：遼寧工程技術大學，2006.

[7]武漢大學測繪學院測量平差學科組.誤差理論與測量平差基礎[M].武漢：武漢大學出版社，2003.

[8]武漢測繪科技大學《測量學》編寫組.測量學[M].北京：測繪出版社，1996.

[9]張述清，等.GPS RTK技術在地籍測量中的應用研究[J].昆明理工大學學報(理工版)，2007，32(2).

[10]熊忠招，田月娥.淺談RTK技術幾種投影在地形圖測量中的應用[J].湖北地礦，2004，18(2).