邊坡變形穩定性中的巖橋效應
李厚恩
(北京市勘察設計研究院有限公司,北京 100038)
邊坡的演化是是非線性的開放系統,它不斷與周圍環境進行著物質和能量交換。同時,邊坡演化是一個漸變的過程,系統內部的相互作用與外部因素影響不斷發生變化,很多國內外學者進行了巨大的努力和探索[1-12],然而,世界上眾多邊坡所帶來的災難說明,對邊坡失穩機制仍需進行進一步深入研究[5]。
對于存在控制性結構面的巖質邊坡而言,其穩定性主要受控于滑動面中巖橋(鎖固段)的性質,如果巖橋不發生剪斷破壞,邊坡失穩亦不會發生。含巖橋結構面的破壞失穩過程屬于斷裂行為,只有當結構面被剪切斷裂貫通后,才有坡體的滑動失穩。對含巖橋結構面起控制性作用的巖質邊坡穩定性計算問題,目前尚缺乏成熟有效的計算手段。當前主要采用經驗方法計算這類邊坡的穩定性,即根據《建筑邊坡工程規范》或《水利水電工程邊坡設計規范》,將結構面的延伸長度折算成連通率,然后采用剛體極限平衡法計算穩定性系數。這種計算方法并未揭示巖橋斷裂破壞對邊坡穩定性的影響,也就使得基于經驗和剛體極限平衡的穩定性計算方法具有先天的缺陷性。而當前對邊坡問題的研究中,也缺乏對巖橋斷裂系統中斷裂的相互作用及能量交換情況的分析。
為分析貫通性結構面形成、發展和破壞的漸進過程,基于摩擦學理論,通過引入彈簧-滑塊組成的Burridge-Knopoff模型(簡稱B-K模型)模擬邊坡問題中巖橋效應對邊坡變形及穩定性的影響。
1 滑面接觸狀況分析
巖體的間接觸面如圖1所示,接觸面的性質決定著其變形的穩定性,可以簡化為圖2所示的模型[13]。
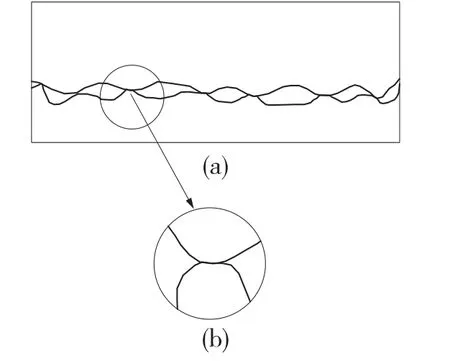
圖1 巖石剪切接觸面粘合示意
圖2中沿接觸面的水平變形由橫向變形x和切向變形z決定;橫向剛度定義為kl=Fl/x,接觸剛度定義為kc=Fc/z;m為接觸部分的質量,其固有頻率定義為靜態作用下,系統的適應性特點有假設導致失穩的潛在作用力與結構面的表面性態相關,可表示為
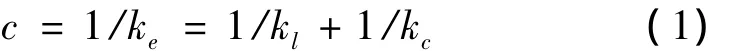
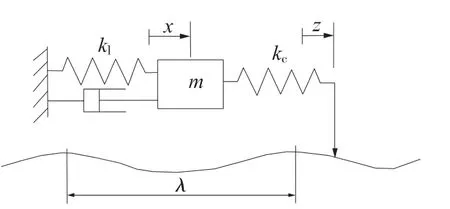
圖2 接觸摩擦的簡化模型
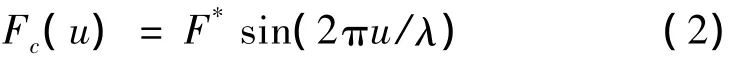
式中,u為切向變形量。當存在粘滯阻力Ff時,有
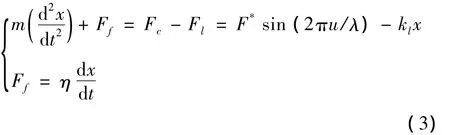
當結構面的變形表示為y(t)=vt,其中v為變形速率,此時,上部巖體的滑動量表示為
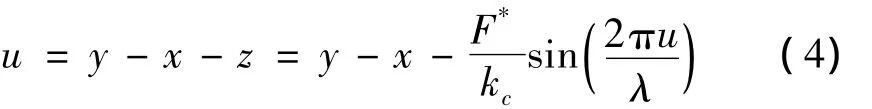
準靜態狀況下(d2x/d t2)=0,因此
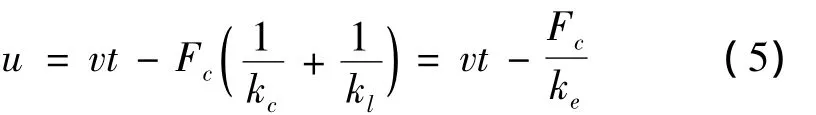
引入無量剛變量
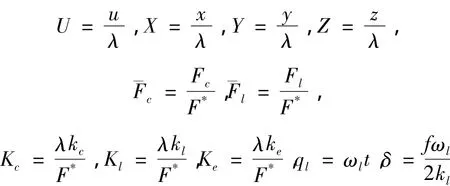
將式(1)和(3)改寫為
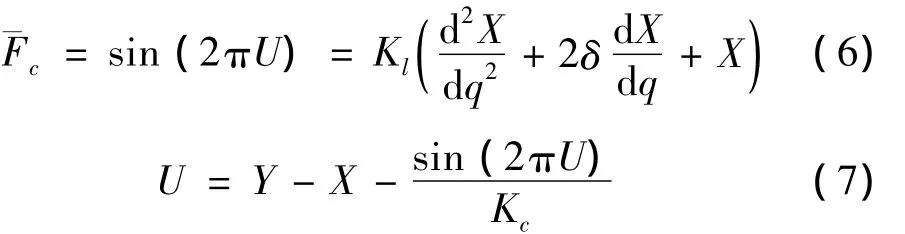
準靜態狀況下,有
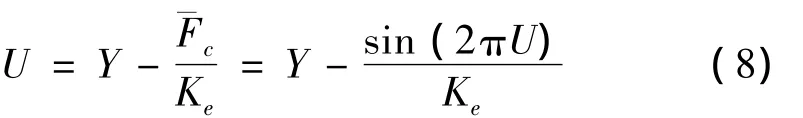
圖3 為 Kl=4、Kc=3、δ=0.1、(2πV/λωl)=15 時的數值結果。圖3中,O點有Fˉc=Fl=X=Z=vt/λ=0,OE為穩定的準靜態過程。切向變形在E變為不穩定點,接觸部位的行為由式(14)所描述,此時曲線斜率的剛度為Ke。在A點,系統發生整體上的失穩,此時曲線斜率所表示的剛度為-Kc。
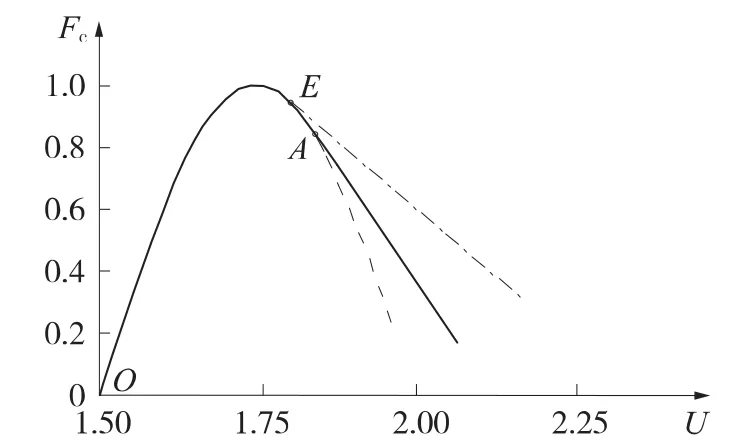
圖3 數值計算結果
2 巖橋效應對邊坡變形影響模擬分析
事實上,邊坡問題與摩擦學密切相關,庫侖莫爾破壞準則可視為對摩擦定律的推廣。圖2所示狀況,利用平均場的理念將其簡化為圖4所示的平面滑動模型。設系統的初始狀態為:彈簧不受力壓縮,而質量m靜止不動。當下部滑體移動時,直到驅動力即彈簧力和阻尼力的合力等于靜止摩擦力時,m才會移動。根據牛頓第二定律,有
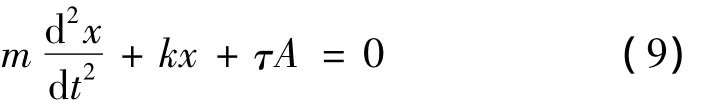
式中,x為彈簧變形量,m為滑塊質量,k為彈簧剛度,τ為摩擦產生的剪切應力,A為接觸面積。
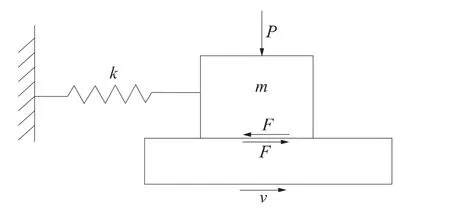
圖4 粘滑模型
對于整個邊坡來說,滑動面可能存在多個巖橋,因此滑面系統用彈簧-滑塊組成的B-K模型[11]來描述,如圖5所示,其中滑塊可用以模擬邊坡巖橋效應。假設上部巖層的變形速率為v,質量為m的滑塊由剛度分別為kc和kl的彈簧與相鄰滑塊和上部巖體相連結,滑塊之間的初始距離為a。圖5所示模型的力學表達式為[14-15]
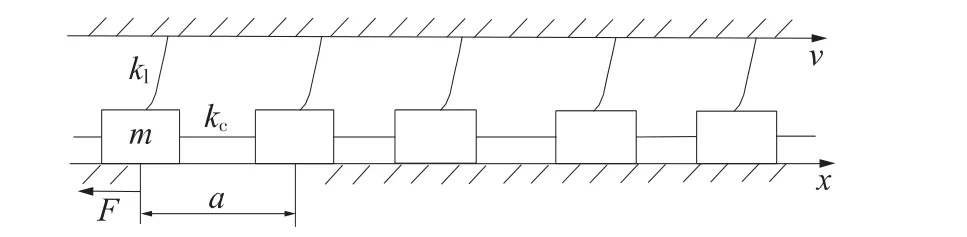
圖5 Burridge-Knopoff模型
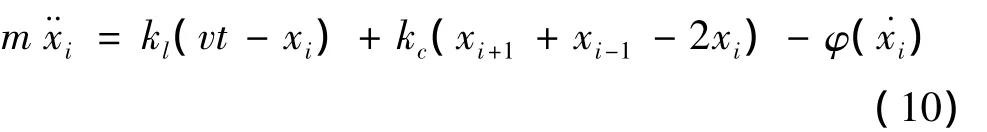
式中,xi為第i個滑塊t時刻的變形量,φ(˙xi)為其對應的摩擦力。
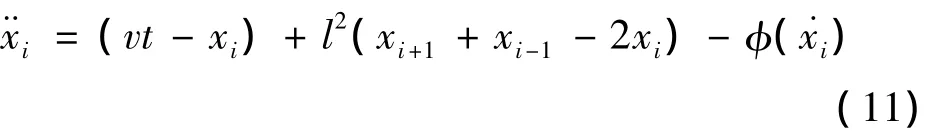
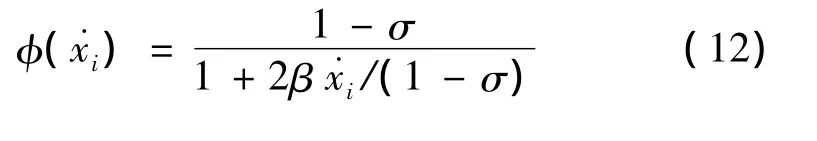
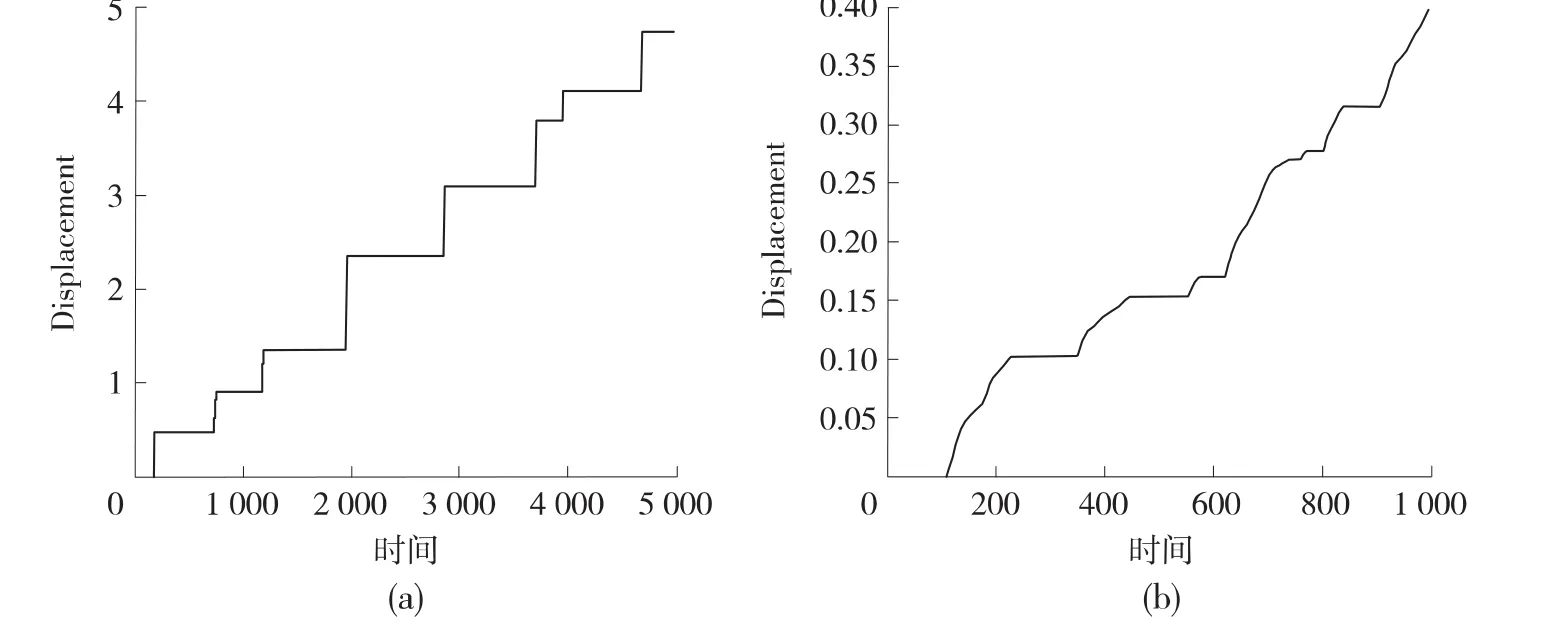
圖6 數值計算結果
事實上,隨著邊坡系統的演化,滑動面上的斷裂結構會由低級別向高級別發展,形成由幾個(或一個)相對堅固的巖橋組成的非貫通性的結構面。因此,隨著邊坡變形量的增加,巖橋數量會減少,此時會由圖6(a)所示的狀況向圖6(b)轉化。
圖7為新灘滑坡A3測點位移監測曲線[12],邊坡變形位移曲線具有顯著的臺階效應,這與圖6所展示的背景圖像具有很好的一致性。
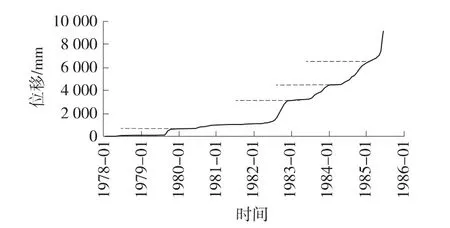
圖7 新灘滑坡發生前A3監測點位移-時間曲線
4 結論
通過以上研究可知,邊坡變形演化過程與潛在滑面上的巖橋(鎖固段)有著密切聯系,通過分析接觸面的力學特性,引入了彈簧-滑塊構成的B-K模型來分析非貫通結構面中的巖橋效應,通過數值計算發現,邊坡的變形特性與巖橋的級別和數量密切相關,當其結構比較簡單時(即巖橋數量較少,級別較大),邊坡的變形與時間背景圖像是比較清晰的。
[1] Skempton A W.Residual strength of clays in landslides,folded strata and the laboratory[J].Geotechnique,1985,35:3-18.
[2] Sornette,D.,Helmstetter,A.,Andersen,J.V.,Gluzman,S.,Grasso,J.R.,Pisarenko,V.,Towards landslide predictions:two case studies[J].Physica,2004,33(8):605-632.
[3] Crosta,G.B.,Agliardi,F.,How to obtain alert velocity thresholds for large rockslides[J]Physics and Chemistry of the Earth,2002,27(a):1557-1565.
[4] Siqing Qin,Jiu Jimmy Jiao,Zhigang Li.Nonlinear evolutionary mechanisms of instability of plane-shear slope:catastrophe,bifurcation,chaos and physical prediction[J] Rock Mechanics and Rock Engineering,2006,39(1):59-76.
[5] Martel,S.J.Mechanics of landslide initiation as a shear fracture phenomenon[J]Marine Geology,2004,20(3):319-339.
[6] Anders Meurk.Microscopic stick - slip in friction force microscopy.Tribology letters,2000(8):161-169
[7] 黃潤秋,張倬元,王士天.黃河拉西瓦水電站高邊坡穩定性的系統工程地質研究[M].成都:成都科技大學出版社,1991
[8] 黃志全,張長存,姜彤,等.滑坡預報得協同-分岔模型及其應用[J].巖石力學與工程學報,2002,21(4):498-501
[9] 徐嘉謨.粘聚力作用在塊體穩定性分析中的意義[M]∥徐嘉謨,等.工程地質力學研究.北京:地質出版社,1985
[10] 張年學,盛祝平,孫廣忠,等.長江三峽工程庫區順層岸坡研究[M].北京:地質出版社,1993
[11] 王來貴,黃潤秋,王泳嘉,等.巖石力學系統運動穩定性理論及其應用[M].北京:地質出版社,1998.
[12] 賀可強,孫林娜,王思敬.滑坡位移分形參數Hurst指數及其在堆積層滑坡預報中的應用[J].巖石力學與工程學報,2009,28(6):1107-1115.
[13] Victor G.BYKOV.Stick-slip and strain waves in the physics of earthquake rupture:experiments and models,Acta Geophysica,2007,56(2):170-280.
[14] Burridge R,Knopoff L Model and theoretical seismicity[J].Bull Seism Soc Amer,1967,57:341-371.
[15] 吳忠良,陳運泰.從彈簧滑塊到地震預測:B-K模型今昔談[J].物理,2002,31(11):719-24.

