從八皇后問題的解決方案看面向過程和面向?qū)ο?/h1>
2012-04-20 09:31:38宋東興殷旭東
常熟理工學(xué)院學(xué)報 2012年4期
宋東興，殷旭東
（常熟理工學(xué)院計算機科學(xué)與工程學(xué)院，江蘇常熟 215500）
從八皇后問題的解決方案看面向過程和面向?qū)ο?/p>
宋東興，殷旭東
（常熟理工學(xué)院計算機科學(xué)與工程學(xué)院，江蘇常熟 215500）
通過八皇后問題的解的分析，討論了面向過程的解決方案和面向?qū)ο蠼鉀Q方案的不同，比較了面向過程設(shè)計思想和面向?qū)ο笤O(shè)計思想的區(qū)別和聯(lián)系，提出程序設(shè)計教學(xué)要從面向過程逐步過渡到面向?qū)ο螅鎻娬{(diào)一面而忽視另一面都是不可取的.
八皇后；面向過程；面向?qū)ο螅粚ο螅唤鉀Q方案
著名數(shù)學(xué)家高斯在1850年提出：在8×8格的國際象棋上擺放八個皇后，使其不能互相攻擊，即任意兩個皇后都不能處于同一行、同一列或同一斜線上，問有多少種擺法？此即八皇后問題.八皇后問題可以采用面向過程和面向?qū)ο髢煞N不同的解決方案.
在眾多針對“軟件危機”[1]的解決方案中，面向?qū)ο缶幊淌且环N優(yōu)秀的方法，國內(nèi)大多數(shù)高校的計算機專業(yè)都開設(shè)了面向?qū)ο蟮某绦蛟O(shè)計課程，有的學(xué)校大一就直接進(jìn)入面向?qū)ο蠼虒W(xué).然而要完全拋棄傳統(tǒng)的面向過程方法，只接受面向?qū)ο蠓椒ú⒉豢茖W(xué)，宏觀上的面向?qū)ο笏枷霃奈⒂^上看仍然是面向過程在實現(xiàn)，離開面向過程的鋪墊而直接進(jìn)入面向?qū)ο螅瑢W(xué)生理解起來往往比較困難，實際教學(xué)效果也不理想.筆者通過八皇后問題的求解案例，分析比較面向過程和面向?qū)ο蟮牟煌岢龀绦蛟O(shè)計教學(xué)要從面向過程循序漸進(jìn)到面向?qū)ο?
1 面向過程的分析方法
1.1 基本思想
以過程作為分析的主題，著重強調(diào)一個系統(tǒng)中發(fā)生的過程以及由一個過程的結(jié)果輸出作為下一個過程輸入的數(shù)據(jù)流動，通過信息流及其狀態(tài)轉(zhuǎn)換來認(rèn)識系統(tǒng)，采用的是“自頂向下，逐步求精”的思維方法，核心思想是：以事件為中心，分析解決問題的步驟，然后用函數(shù)把這些步驟一步一步實現(xiàn)，使用時依次調(diào)用就可以了.
1.2 八皇后問題的面向過程的解決方案
需要使用各種數(shù)據(jù)結(jié)構(gòu)來保持棋子的位置，算法通過系統(tǒng)地控制每一個數(shù)據(jù)結(jié)構(gòu)的數(shù)值，檢測每個新位置是否符合沒有皇后攻擊其他皇后的原則來解決問題.
1.2.1 窮舉法
解決八皇后問題的關(guān)鍵在于：
（1）找到合理的數(shù)據(jù)結(jié)構(gòu)存放棋子的擺放位置.
（2）要有合理的沖突檢查算法[2].采用的方法是，先把8個棋子擺在棋盤上，每行擺一個，然后去檢查這種擺放是否有沖突，如果沒有沖突，即找到了一種解決方案.
首先是如何存放棋子的擺放位置.可以設(shè)想一下，當(dāng)8個棋子擺放好之后，每個棋子的位置都有一個行值和列值，由于每行只有一個棋子，就可以從第0行開始依次記錄每個棋子的列值，8個棋子的列值依次排列構(gòu)成一個數(shù)字序列，例如24135046，它表示第0行棋子擺放在第2列，第1行棋子擺放在第4列，以此類推，這樣一種擺放方式對應(yīng)一個8位的8進(jìn)制數(shù)，用一個一維數(shù)組來存放這樣一個8進(jìn)制數(shù)，00000000-77777777窮舉了所有的擺放方式.
接下來對每種擺放情況做沖突檢查，若不沖突就是一個解.
注：(i，queen[i])代表一個棋子的行，列坐標(biāo).
沖突檢查：（1）每行只放一個棋子，行上不會有沖突.
（2）數(shù)組中如沒有兩個元素值相同，則列上沒有沖突.
（3）任意兩個棋子（i，queen[i]），(j，queen[j])，只要有queen[i]+i!=queen[j]+j，且queen[i]-i!=queen [j]-j，則對角線上沒有沖突.
為方便運算：將八進(jìn)制數(shù)范圍00000000-77777777表達(dá)成十進(jìn)制，則范圍為[0，88-1]，再將范圍內(nèi)每個十進(jìn)制數(shù)轉(zhuǎn)化為八進(jìn)制數(shù)字存入queen數(shù)組中.
窮舉算法：
1.2.2 回溯法[3]
回溯算法也叫試探法，它是一種系統(tǒng)化的窮舉搜索問題的解的方法，基本思想是：從一條路往前走，能進(jìn)則進(jìn)，不能進(jìn)則退回來，換一條路再試.在前進(jìn)和回撤的路上都設(shè)置一些標(biāo)記，以便正確返回，直到達(dá)到目標(biāo)或者所有可能方案都已嘗試為止.
從第一行開始，逐行安排皇后（Q），Q1從第一行的第一個位置開始嘗試，然后嘗試Q2，…Qi-1，使得前i-1個皇后互不攻擊，再嘗試Qi，如果第i行上沒有剩余可放位置，則返回i-1行，同時使Qi-1放棄剛才擺放位置，并嘗試下一位置，…當(dāng)Q8成功放置時，則找到一種解.當(dāng)Q8嘗試過最后一行的所有位置后，算法結(jié)束.
回溯算法：
2 面向?qū)ο蟮姆治龇椒?/h2>
2.1 基本思想
面向?qū)ο蠓治龇椒ǖ幕舅枷胧牵喝f物都可看作對象[4]，面向?qū)ο蟮南到y(tǒng)是由一組互相作用的對象所組成的一個團(tuán)體，每一個對象都扮演一個角色，并為團(tuán)體中的其他成員提供特定的服務(wù)或者執(zhí)行特定的行為，目標(biāo)的實現(xiàn)來自于每個對象的努力和他們之間的相互協(xié)作.
2.2 八皇后問題的面向?qū)ο蟮慕鉀Q方案
方案要點：創(chuàng)建代表每一個皇后的對象，然后賦予它們尋找解決方案的能力，八個皇后彼此之間相互作用，各自負(fù)責(zé)尋找自己的解決方案[1].
2.2.1 為皇后對象建模
分析：在任一解決方案中，不會出現(xiàn)空列，一列也不可能有兩個皇后，可以為每一皇后指定一個特定列（col），而尋找一個合適的行（row）.為了找到解決方案，皇后們需要相互聯(lián)系，每個皇后只需要了解它的鄰居（neighbor），即緊挨著其左邊的那個皇后.
第n列的可接受的解決方案可表示為：從第1列到第n列，沒有皇后可以攻擊其他皇后.每個皇后只需詢問相鄰皇后是否能夠互相攻擊.如果能夠互相攻擊，那么這個皇后就前進(jìn)一行（如不能前進(jìn)將返回失敗），當(dāng)相鄰皇后返回不能互相攻擊的信息時，解決方案就找到了，通過詢問最右端的皇后，找到一個可能的解決方案，即可找到整個問題的方案.
2.2.2 Queen類的部分方法實現(xiàn)思路
①構(gòu)造方法
為皇后對象建立必需的初始條件，行（row）從第0列開始，處于第n列皇后通過給定列號（col）以及相鄰的皇后進(jìn)行初始化.
圖1 皇后類的UML表示
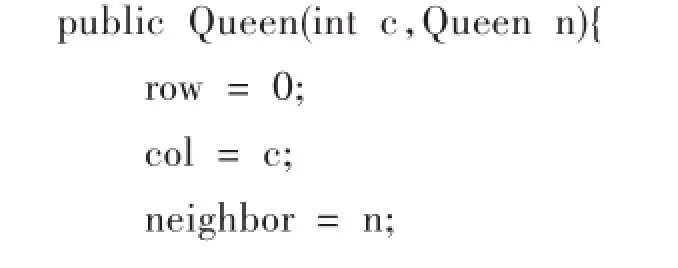
②尋找解決方案findsolution()
通過詢問相鄰皇后是否能夠互相攻擊，來尋找解決方案.如果能夠互相攻擊，那么這個皇后就前進(jìn)一行（如不能前進(jìn)將返回失敗），當(dāng)相鄰皇后返回不能互相攻擊的信息時，解決方案就找到了.
③皇后前進(jìn)下一位置advance()
如果當(dāng)前不是最后行，則行號（row）加1，否則當(dāng)試驗過本列所有位置后仍然沒有找到解決方案時，就要求鄰居皇后尋找新的解決方案，并且自己的行（row）位置重新從第0行開始.
2.2.3 八皇后問題的面向?qū)ο蠼?/p>
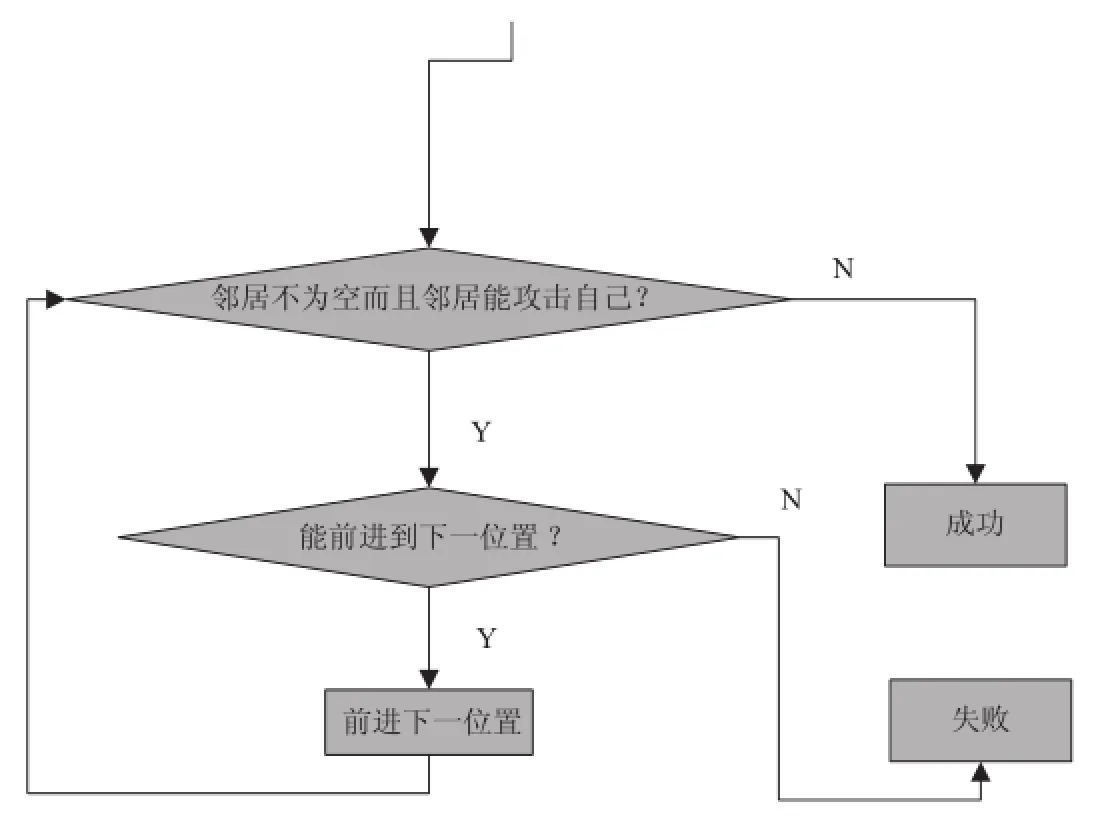
圖2 findSolution()方法實現(xiàn)思路
3 面向過程和面向?qū)ο蟮慕鉀Q方案比較
從八皇后的問題的解法來看，傳統(tǒng)的面向過程的求解就像一個人坐在棋盤前，移動一些毫無生命的棋子，這種方式強調(diào)的是從一個行為到另一個行為的控制流，每一步過程的結(jié)果，都是下一步的前提條件，程序設(shè)計者必須事必躬親，考慮系統(tǒng)的每一細(xì)節(jié)，什么時候?qū)κ裁磾?shù)據(jù)進(jìn)行操作.當(dāng)分析的系統(tǒng)規(guī)模較小時，面向過程的方法能取得較好的效果，但當(dāng)系統(tǒng)逐比較大復(fù)雜時，由于系統(tǒng)組成預(yù)先不可知，加上系統(tǒng)組成之間的結(jié)構(gòu)關(guān)系也不易弄清楚的情況下，面向過程的分析方法就難以勝任了.
而在八皇后問題的面向?qū)ο蟮慕夥ㄖ校覀冑x予每一個棋子自己解決問題的能力[1].把尋找解決方案的責(zé)任分配給那些相互作用的皇后對象，每一個棋子就像一個有生命的個體，它們彼此相互作用，各自負(fù)責(zé)尋找自己的解決方案，這代替了那種由單一實體來控制結(jié)果的集中模式，當(dāng)系統(tǒng)需求增加或發(fā)生變化時，只需在局部進(jìn)行改變或增刪操作，而不會影響整個系統(tǒng)的架構(gòu).
面向過程方法要求你為數(shù)據(jù)結(jié)構(gòu)做些什么，而面向?qū)ο蟮姆椒▌t問數(shù)據(jù)結(jié)構(gòu)為你做了些什么；面向過程采用的是一個過程狀態(tài)轉(zhuǎn)換模型，它與實際計算機內(nèi)部的工作流程大致相吻合，但對于我們理解如何使用計算機來解決問題卻沒有什么幫助，面向過程采用的是“責(zé)任驅(qū)動”設(shè)計模型，與現(xiàn)實世界人們解決問題的方式相近，但無論是哪種方式對程序員來說都應(yīng)該熟悉和掌握.教師在面向?qū)ο蟮某绦蛟O(shè)計教學(xué)中，選取一些典型的問題，引導(dǎo)學(xué)生用兩種不同方式來思考解決，更有利于學(xué)生加深對面向?qū)ο蟮乃季S方式的理解，筆者在實際的教學(xué)中采用這種方式也取得了較好的效果.
4 結(jié)束語
面向過程和面向?qū)ο笫莾煞N不同的思考問題的方法，面向過程方法以事務(wù)為中心，側(cè)重于分析解決問題所需的步驟，強調(diào)怎么實施，而面向?qū)ο笫且允挛餅橹行模严到y(tǒng)分解成若干對象，側(cè)重某個對象在整個解決問題的過程中的責(zé)任（行為），強調(diào)實施什么.通過用責(zé)任來討論問題，提高了抽象的水平，使得對象之間更加獨立，這正是解決復(fù)雜問題的關(guān)鍵.
對于大多數(shù)問題，面向?qū)ο蠓椒ū让嫦蜻^程方法優(yōu)越，但并不意味著它能完全取代面向過程，事實上，從宏觀角度來分析系統(tǒng)時采用面向?qū)ο螅鴱奈⒂^考慮一個對象的行為的具體實現(xiàn)時，離不開面向過程[5].這就要求程序設(shè)計課程教學(xué)要從面向過程開始，并在教學(xué)中及時滲透面向?qū)ο蟮乃枷耄箤W(xué)生逐步過渡到用面向?qū)ο蠓椒ㄋ伎紗栴}.
[1]（美）Timothy A Budd.面向?qū)ο蟪绦蛟O(shè)計（影印版）[M].北京：清華大學(xué)出版社，2004.
[2]焦玲，邢偉，于海波，等.Java程序設(shè)計案例匯編[M].北京：中國鐵道出版社，2008.
[3]嚴(yán)蔚敏，吳偉民.數(shù)據(jù)結(jié)構(gòu)（C語言版）[M].北京：清華大學(xué)出版社，1997.
[4]（美）Bruce Eckel.Java編程思想[M].北京：機械工業(yè)出版社，2005.
[5]游曉明，劉升.面向過程向面向?qū)ο蟪绦蛟O(shè)計的轉(zhuǎn)變與實現(xiàn)[J].湖北師范學(xué)院學(xué)報，1999（2）.
Observing Procedure-oriented and Object-oriented from the Solution to the Eight-queen Puzzle
SONG Dong-xing,Ying Xu-dong,LIU Yong-jun
(School of Computer Science and Engineering,Changshu Institute of Technology,Changshu 215500,China)
By analyzing the question of the eight-queen puzzle,this paper discusses the different solutions between procedure-oriented and object-oriented,compares their relation and difference.The paper also proposes program?ming design teaching,which needs natural transition from procedure-oriented to object-oriented,and it is not desir?able to emphasize one side and ignore another one.
eight queens;procedure-oriented;object-oriented;object;solution
TP312
A
1008-2794（2012）04-0120-05
2012-02-23
宋東興（1973—），男，江蘇高郵人，講師，研究方向：計算機網(wǎng)絡(luò)技術(shù)，圖像處理，軟件工程.
猜你喜歡
艾默生自動化解決方案儀器儀表用戶(2022年4期)2022-04-01 03:17:14 解決方案和折中方案閱讀與作文(英語初中版)(2021年8期)2021-09-13 02:16:29 學(xué)習(xí)方法兒童故事畫報(2019年5期)2019-05-26 14:26:14 用對方法才能瘦Coco薇(2016年2期)2016-03-22 02:42:52 4G LTE室內(nèi)覆蓋解決方案探討數(shù)字通信世界(2015年10期)2015-12-21 12:22:54 四大方法 教你不再“坐以待病”！Coco薇(2015年1期)2015-08-13 02:47:34 賺錢方法小雪花·成長指南(2015年7期)2015-08-11 15:03:12 捕魚小雪花·成長指南(2015年4期)2015-05-19 14:47:56 7大睡眠問題解決方案母子健康(2015年1期)2015-02-28 11:21:44 Moxa 802.11n WLAN解決方案AWK-1131A系列自動化博覽(2014年10期)2014-02-28 22:33:42
宋東興，殷旭東
（常熟理工學(xué)院計算機科學(xué)與工程學(xué)院，江蘇常熟 215500）
從八皇后問題的解決方案看面向過程和面向?qū)ο?/p>
宋東興，殷旭東
（常熟理工學(xué)院計算機科學(xué)與工程學(xué)院，江蘇常熟 215500）
通過八皇后問題的解的分析，討論了面向過程的解決方案和面向?qū)ο蠼鉀Q方案的不同，比較了面向過程設(shè)計思想和面向?qū)ο笤O(shè)計思想的區(qū)別和聯(lián)系，提出程序設(shè)計教學(xué)要從面向過程逐步過渡到面向?qū)ο螅鎻娬{(diào)一面而忽視另一面都是不可取的.
八皇后；面向過程；面向?qū)ο螅粚ο螅唤鉀Q方案
著名數(shù)學(xué)家高斯在1850年提出：在8×8格的國際象棋上擺放八個皇后，使其不能互相攻擊，即任意兩個皇后都不能處于同一行、同一列或同一斜線上，問有多少種擺法？此即八皇后問題.八皇后問題可以采用面向過程和面向?qū)ο髢煞N不同的解決方案.
在眾多針對“軟件危機”[1]的解決方案中，面向?qū)ο缶幊淌且环N優(yōu)秀的方法，國內(nèi)大多數(shù)高校的計算機專業(yè)都開設(shè)了面向?qū)ο蟮某绦蛟O(shè)計課程，有的學(xué)校大一就直接進(jìn)入面向?qū)ο蠼虒W(xué).然而要完全拋棄傳統(tǒng)的面向過程方法，只接受面向?qū)ο蠓椒ú⒉豢茖W(xué)，宏觀上的面向?qū)ο笏枷霃奈⒂^上看仍然是面向過程在實現(xiàn)，離開面向過程的鋪墊而直接進(jìn)入面向?qū)ο螅瑢W(xué)生理解起來往往比較困難，實際教學(xué)效果也不理想.筆者通過八皇后問題的求解案例，分析比較面向過程和面向?qū)ο蟮牟煌岢龀绦蛟O(shè)計教學(xué)要從面向過程循序漸進(jìn)到面向?qū)ο?
1 面向過程的分析方法
1.1 基本思想
以過程作為分析的主題，著重強調(diào)一個系統(tǒng)中發(fā)生的過程以及由一個過程的結(jié)果輸出作為下一個過程輸入的數(shù)據(jù)流動，通過信息流及其狀態(tài)轉(zhuǎn)換來認(rèn)識系統(tǒng)，采用的是“自頂向下，逐步求精”的思維方法，核心思想是：以事件為中心，分析解決問題的步驟，然后用函數(shù)把這些步驟一步一步實現(xiàn)，使用時依次調(diào)用就可以了.
1.2 八皇后問題的面向過程的解決方案
需要使用各種數(shù)據(jù)結(jié)構(gòu)來保持棋子的位置，算法通過系統(tǒng)地控制每一個數(shù)據(jù)結(jié)構(gòu)的數(shù)值，檢測每個新位置是否符合沒有皇后攻擊其他皇后的原則來解決問題.
1.2.1 窮舉法
解決八皇后問題的關(guān)鍵在于：
（1）找到合理的數(shù)據(jù)結(jié)構(gòu)存放棋子的擺放位置.
（2）要有合理的沖突檢查算法[2].采用的方法是，先把8個棋子擺在棋盤上，每行擺一個，然后去檢查這種擺放是否有沖突，如果沒有沖突，即找到了一種解決方案.
首先是如何存放棋子的擺放位置.可以設(shè)想一下，當(dāng)8個棋子擺放好之后，每個棋子的位置都有一個行值和列值，由于每行只有一個棋子，就可以從第0行開始依次記錄每個棋子的列值，8個棋子的列值依次排列構(gòu)成一個數(shù)字序列，例如24135046，它表示第0行棋子擺放在第2列，第1行棋子擺放在第4列，以此類推，這樣一種擺放方式對應(yīng)一個8位的8進(jìn)制數(shù)，用一個一維數(shù)組來存放這樣一個8進(jìn)制數(shù)，00000000-77777777窮舉了所有的擺放方式.
接下來對每種擺放情況做沖突檢查，若不沖突就是一個解.
注：(i，queen[i])代表一個棋子的行，列坐標(biāo).
沖突檢查：（1）每行只放一個棋子，行上不會有沖突.
（2）數(shù)組中如沒有兩個元素值相同，則列上沒有沖突.
（3）任意兩個棋子（i，queen[i]），(j，queen[j])，只要有queen[i]+i!=queen[j]+j，且queen[i]-i!=queen [j]-j，則對角線上沒有沖突.
為方便運算：將八進(jìn)制數(shù)范圍00000000-77777777表達(dá)成十進(jìn)制，則范圍為[0，88-1]，再將范圍內(nèi)每個十進(jìn)制數(shù)轉(zhuǎn)化為八進(jìn)制數(shù)字存入queen數(shù)組中.
窮舉算法：
1.2.2 回溯法[3]
回溯算法也叫試探法，它是一種系統(tǒng)化的窮舉搜索問題的解的方法，基本思想是：從一條路往前走，能進(jìn)則進(jìn)，不能進(jìn)則退回來，換一條路再試.在前進(jìn)和回撤的路上都設(shè)置一些標(biāo)記，以便正確返回，直到達(dá)到目標(biāo)或者所有可能方案都已嘗試為止.
從第一行開始，逐行安排皇后（Q），Q1從第一行的第一個位置開始嘗試，然后嘗試Q2，…Qi-1，使得前i-1個皇后互不攻擊，再嘗試Qi，如果第i行上沒有剩余可放位置，則返回i-1行，同時使Qi-1放棄剛才擺放位置，并嘗試下一位置，…當(dāng)Q8成功放置時，則找到一種解.當(dāng)Q8嘗試過最后一行的所有位置后，算法結(jié)束.
回溯算法：
2 面向?qū)ο蟮姆治龇椒?/h2>
2.1 基本思想
面向?qū)ο蠓治龇椒ǖ幕舅枷胧牵喝f物都可看作對象[4]，面向?qū)ο蟮南到y(tǒng)是由一組互相作用的對象所組成的一個團(tuán)體，每一個對象都扮演一個角色，并為團(tuán)體中的其他成員提供特定的服務(wù)或者執(zhí)行特定的行為，目標(biāo)的實現(xiàn)來自于每個對象的努力和他們之間的相互協(xié)作.
2.2 八皇后問題的面向?qū)ο蟮慕鉀Q方案
方案要點：創(chuàng)建代表每一個皇后的對象，然后賦予它們尋找解決方案的能力，八個皇后彼此之間相互作用，各自負(fù)責(zé)尋找自己的解決方案[1].
2.2.1 為皇后對象建模
分析：在任一解決方案中，不會出現(xiàn)空列，一列也不可能有兩個皇后，可以為每一皇后指定一個特定列（col），而尋找一個合適的行（row）.為了找到解決方案，皇后們需要相互聯(lián)系，每個皇后只需要了解它的鄰居（neighbor），即緊挨著其左邊的那個皇后.
第n列的可接受的解決方案可表示為：從第1列到第n列，沒有皇后可以攻擊其他皇后.每個皇后只需詢問相鄰皇后是否能夠互相攻擊.如果能夠互相攻擊，那么這個皇后就前進(jìn)一行（如不能前進(jìn)將返回失敗），當(dāng)相鄰皇后返回不能互相攻擊的信息時，解決方案就找到了，通過詢問最右端的皇后，找到一個可能的解決方案，即可找到整個問題的方案.
2.2.2 Queen類的部分方法實現(xiàn)思路
①構(gòu)造方法
為皇后對象建立必需的初始條件，行（row）從第0列開始，處于第n列皇后通過給定列號（col）以及相鄰的皇后進(jìn)行初始化.
圖1 皇后類的UML表示
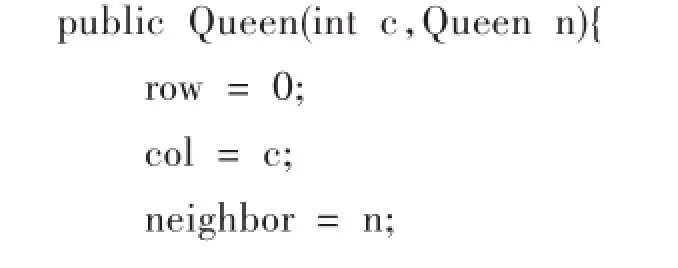
②尋找解決方案findsolution()
通過詢問相鄰皇后是否能夠互相攻擊，來尋找解決方案.如果能夠互相攻擊，那么這個皇后就前進(jìn)一行（如不能前進(jìn)將返回失敗），當(dāng)相鄰皇后返回不能互相攻擊的信息時，解決方案就找到了.
③皇后前進(jìn)下一位置advance()
如果當(dāng)前不是最后行，則行號（row）加1，否則當(dāng)試驗過本列所有位置后仍然沒有找到解決方案時，就要求鄰居皇后尋找新的解決方案，并且自己的行（row）位置重新從第0行開始.
2.2.3 八皇后問題的面向?qū)ο蠼?/p>
圖2 findSolution()方法實現(xiàn)思路
3 面向過程和面向?qū)ο蟮慕鉀Q方案比較
從八皇后的問題的解法來看，傳統(tǒng)的面向過程的求解就像一個人坐在棋盤前，移動一些毫無生命的棋子，這種方式強調(diào)的是從一個行為到另一個行為的控制流，每一步過程的結(jié)果，都是下一步的前提條件，程序設(shè)計者必須事必躬親，考慮系統(tǒng)的每一細(xì)節(jié)，什么時候?qū)κ裁磾?shù)據(jù)進(jìn)行操作.當(dāng)分析的系統(tǒng)規(guī)模較小時，面向過程的方法能取得較好的效果，但當(dāng)系統(tǒng)逐比較大復(fù)雜時，由于系統(tǒng)組成預(yù)先不可知，加上系統(tǒng)組成之間的結(jié)構(gòu)關(guān)系也不易弄清楚的情況下，面向過程的分析方法就難以勝任了.
而在八皇后問題的面向?qū)ο蟮慕夥ㄖ校覀冑x予每一個棋子自己解決問題的能力[1].把尋找解決方案的責(zé)任分配給那些相互作用的皇后對象，每一個棋子就像一個有生命的個體，它們彼此相互作用，各自負(fù)責(zé)尋找自己的解決方案，這代替了那種由單一實體來控制結(jié)果的集中模式，當(dāng)系統(tǒng)需求增加或發(fā)生變化時，只需在局部進(jìn)行改變或增刪操作，而不會影響整個系統(tǒng)的架構(gòu).
面向過程方法要求你為數(shù)據(jù)結(jié)構(gòu)做些什么，而面向?qū)ο蟮姆椒▌t問數(shù)據(jù)結(jié)構(gòu)為你做了些什么；面向過程采用的是一個過程狀態(tài)轉(zhuǎn)換模型，它與實際計算機內(nèi)部的工作流程大致相吻合，但對于我們理解如何使用計算機來解決問題卻沒有什么幫助，面向過程采用的是“責(zé)任驅(qū)動”設(shè)計模型，與現(xiàn)實世界人們解決問題的方式相近，但無論是哪種方式對程序員來說都應(yīng)該熟悉和掌握.教師在面向?qū)ο蟮某绦蛟O(shè)計教學(xué)中，選取一些典型的問題，引導(dǎo)學(xué)生用兩種不同方式來思考解決，更有利于學(xué)生加深對面向?qū)ο蟮乃季S方式的理解，筆者在實際的教學(xué)中采用這種方式也取得了較好的效果.
4 結(jié)束語
面向過程和面向?qū)ο笫莾煞N不同的思考問題的方法，面向過程方法以事務(wù)為中心，側(cè)重于分析解決問題所需的步驟，強調(diào)怎么實施，而面向?qū)ο笫且允挛餅橹行模严到y(tǒng)分解成若干對象，側(cè)重某個對象在整個解決問題的過程中的責(zé)任（行為），強調(diào)實施什么.通過用責(zé)任來討論問題，提高了抽象的水平，使得對象之間更加獨立，這正是解決復(fù)雜問題的關(guān)鍵.
對于大多數(shù)問題，面向?qū)ο蠓椒ū让嫦蜻^程方法優(yōu)越，但并不意味著它能完全取代面向過程，事實上，從宏觀角度來分析系統(tǒng)時采用面向?qū)ο螅鴱奈⒂^考慮一個對象的行為的具體實現(xiàn)時，離不開面向過程[5].這就要求程序設(shè)計課程教學(xué)要從面向過程開始，并在教學(xué)中及時滲透面向?qū)ο蟮乃枷耄箤W(xué)生逐步過渡到用面向?qū)ο蠓椒ㄋ伎紗栴}.
[1]（美）Timothy A Budd.面向?qū)ο蟪绦蛟O(shè)計（影印版）[M].北京：清華大學(xué)出版社，2004.
[2]焦玲，邢偉，于海波，等.Java程序設(shè)計案例匯編[M].北京：中國鐵道出版社，2008.
[3]嚴(yán)蔚敏，吳偉民.數(shù)據(jù)結(jié)構(gòu)（C語言版）[M].北京：清華大學(xué)出版社，1997.
[4]（美）Bruce Eckel.Java編程思想[M].北京：機械工業(yè)出版社，2005.
[5]游曉明，劉升.面向過程向面向?qū)ο蟪绦蛟O(shè)計的轉(zhuǎn)變與實現(xiàn)[J].湖北師范學(xué)院學(xué)報，1999（2）.
Observing Procedure-oriented and Object-oriented from the Solution to the Eight-queen Puzzle
SONG Dong-xing,Ying Xu-dong,LIU Yong-jun
(School of Computer Science and Engineering,Changshu Institute of Technology,Changshu 215500,China)
By analyzing the question of the eight-queen puzzle,this paper discusses the different solutions between procedure-oriented and object-oriented,compares their relation and difference.The paper also proposes program?ming design teaching,which needs natural transition from procedure-oriented to object-oriented,and it is not desir?able to emphasize one side and ignore another one.
eight queens;procedure-oriented;object-oriented;object;solution
TP312
A
1008-2794（2012）04-0120-05
2012-02-23
宋東興（1973—），男，江蘇高郵人，講師，研究方向：計算機網(wǎng)絡(luò)技術(shù)，圖像處理，軟件工程.
猜你喜歡
儀器儀表用戶(2022年4期)2022-04-01 03:17:14
閱讀與作文(英語初中版)(2021年8期)2021-09-13 02:16:29
兒童故事畫報(2019年5期)2019-05-26 14:26:14
Coco薇(2016年2期)2016-03-22 02:42:52
數(shù)字通信世界(2015年10期)2015-12-21 12:22:54
Coco薇(2015年1期)2015-08-13 02:47:34
小雪花·成長指南(2015年7期)2015-08-11 15:03:12
小雪花·成長指南(2015年4期)2015-05-19 14:47:56
母子健康(2015年1期)2015-02-28 11:21:44
自動化博覽(2014年10期)2014-02-28 22:33:42
