銀行客戶到訪的非泊松性

李 超， 郭進利

（上海理工大學管理學院，上海 200093）

人每天要做很多事情，包括收發電子郵件、前往銀行處理金融事務等.除了明顯的每日或季節性周期以外，找到人類動力學的規律似乎是困難的.在過去的100年中，對人類行為的研究一直是社會學、心理學、經濟學等學科共同關注的問題［1］，但人類自身的復雜性和多樣性，對一切科學的嘗試來說都是巨大的挑戰.事實上，過去學科的絕大多數命題和結論都是定性描述［2］.早前的研究中，由于數據量比較小，且人類行為具有很多隨機性，因此均假設人類行為的發生是隨機和穩態的，即可以看作一個泊松過程.此模型中，對于某給定的個體，連續兩次行為之間的間隔時間分布是一個指數分布［3］.Barabási等從記錄人類活動歷史的數據庫中挖掘出人類行為的統計規律，發現人類行為所呈現出的規律并不與泊松過程一致：很長時間內可能了無一事，而這些長長的空白與空白之間則被陣發的密集活動所填充［4］，呈現胖尾分布，且冪指數大多分布在1～3之間.文獻［5］給出評論時間間隔分布的實證研究，發現人們對于某個話題的興趣逐漸消失，評論的時間間隔服從冪律分布，提出了一個興趣逐漸消失的人類行為動力學模型.文獻［6］對錢學森的郵件通訊記錄進行了統計，統計結果表明其郵件回復時間間隔分布和寫信時間間隔分布均具有冪律的胖尾規律，但已經超出了普適類的范圍.文獻［7］從群體和個人兩個角度，分析借閱過程中圖書的借閱時間和用戶連續兩次借閱或還回圖書的時間間隔等統計特征，探尋群體行為與個體行為的關系.

訪問銀行辦理業務，是人的行為之一.近來，銀行客戶排隊問題越來越受到各方的關注，國家監管部門和各家銀行紛紛出臺各種措施來緩解排隊等候現象.然而，國內市場研究公司CTR于2007年進行的調查表明，排隊問題在大多數銀行仍普遍存在，國有四大行平均等候41min，而在5家股份制銀行平均等候14min.為分析銀行排隊問題，文獻［8］用蒙特卡洛模擬對銀行柜臺多服務器單隊列（M／M／C）的服務狀況進行了動態模擬，提出在不同的服務強度水平下，當到達速率不同時的服務對策，為改進商業銀行客戶服務水平提供參考.文獻［9］利用銀行叫號機實測隊長系列排隊數據，運用排隊論所給出的改善銀行排隊狀況的窗口設置設想與例證，可以作為銀行排隊管理改善的依據和一種簡易可行的方法.目前大部分研究都用到了一個重要假設：銀行客戶到訪是一個泊松過程.現有的研究還沒有對銀行客戶到訪間隔時間分布進行分析，本文根據某銀行網點客戶到達時間的真實記錄，深入挖掘銀行客戶到訪的時間間隔分布、細分客戶到訪的時間間隔分布、單日所有客戶到訪的時間間隔分布的統計特征，發現銀行客戶到訪的時間間隔分布并非指數分布，而是滿足陣發性的冪律分布.

本文的發現有助于理解社會中人群到訪的行為特征，為建立針對冪律事件間隔分布的排隊理論奠定實證基礎，具有重要的理論意義，同時為解決銀行排隊擁擠問題作出理論探索，具有一定的商業化潛力.由于社會中廣泛存在類似于銀行客戶到訪的顧客到達行為，結合原有針對社會系統的實證研究，這些統計結果暗示從復雜的人類行為中可以揭示普遍的規律，發現支配人類活動時間選擇的機制，并獲得控制和預測人類行為的能力.這必將具有重大的實用化潛力.

1 數據來源與統計方法

通過人工統計某月國內某銀行網點大廳（營業時間為8：30～16：30，中午保留少量窗口，周末照常營業）叫號機吐出的每張小票的數據，以每個客戶的真實到達時間為研究對象.該數據庫中客戶到訪共10 403人次，客戶所辦業務可分成7類，分別用A（個人業務）、B（理財業務）、G（公司業務）、J（公司解現）、W（外幣業務）、V（VIP客戶）、T（領取吞卡）作為代表.記錄每個客戶所得小票的打印時間，精確到秒，以此作為到達時間，跨度為某月1日到19日.各個客戶所辦業務的詳細資料如表1所示，比較大的數據量足夠反映真實的統計規律.為簡便起見，對冪律分布的判斷分析用一元線性回歸和最小二乘法得到擬合直線的斜率即冪指數.

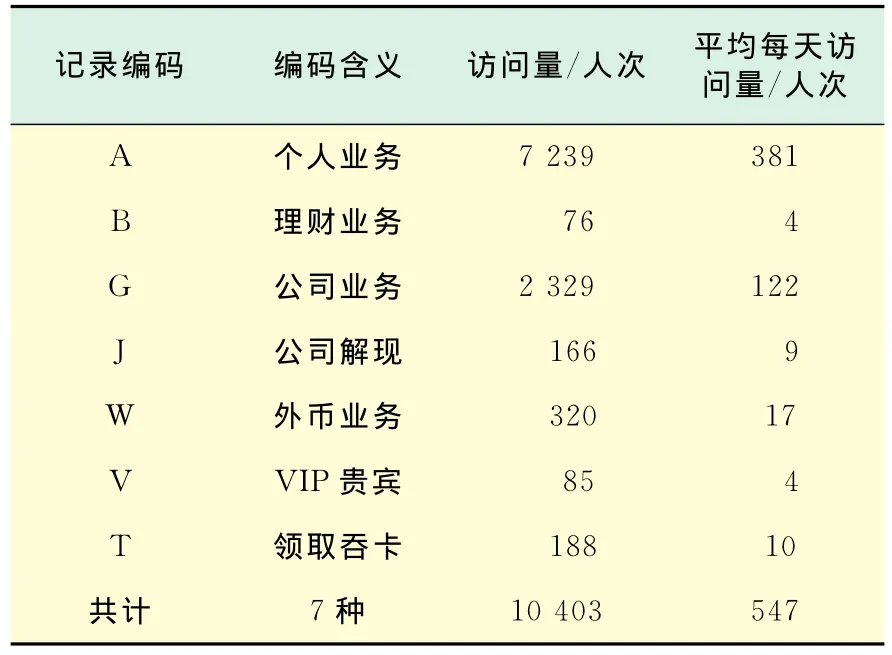
表1 19天中客戶到達時間記錄數據概況Tab.1 Records of customer arrival time in 19days

圖1顯示的是在19天的時間范圍內每天各個時刻所有客戶的訪問量.由于一部分客戶會在銀行剛開門和馬上要關門時進入大廳，因此統計8：00～17：00每小時的客戶訪問量.所有客戶訪問銀行具有明顯的規律性，每天的訪問量曲線形狀大致相同呈“M”形狀，波峰和波谷出現在大致相同的時刻.其中，休息日的訪問量要明顯少于工作日.另外，銀行訪問還表現出明顯的波動性.統計發現客戶訪問量的幾個峰值出現在10：00～11：00、13：00～14：00兩個時間段.顯然，兩個時間段是個人及公司前往銀行辦理事務的高峰期，也是人類一天中活動的活躍期.訪問量的低谷出現在12：00～13：00的中午休息時間和16：00～17：00銀行即將停止營業這一個時間段.這樣的統計規律與客戶工作生活的時間規律很好吻合.

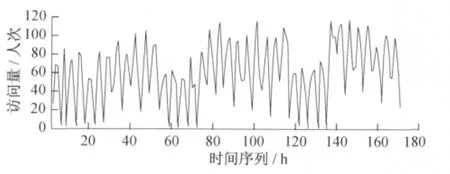
圖1 19天內各個時刻的客戶訪問量Fig.1 Customer visits per hour in 19days

為消除銀行晚上不營業這一明顯事實對客戶到訪間隔時間的影響，對數據作如下處理：第二天第一個客戶的到訪間隔時間將減去16h（銀行從16：30到第二天8：30不營業）.由于一部分客戶會在8：30之前進入大廳，若作差后的間隔時間小于0，則認為該客戶的到達間隔時間為1s，這樣多天的客戶到訪可以看成是一個連續的過程.經過對比，后文出現的概率分布圖的趨勢在數據處理前后都無明顯改變.圖2顯示的是數據處理后，19天內所有客戶到訪間隔時間圖，圖中τ表示間隔時間.注意那些最長的像長釘一樣扎在水平軸上的豎線，它們對應于那些很長的到訪間隔時間（可以長達近2h）.這些最長的豎線是以周為周期出現的，并且都是出現在休息日的中午時間段，表明休息日中午幾乎沒有客戶前往銀行辦理業務.而對比工作日中午銀行仍有客戶連續到訪，但到訪量相比每天的高峰時段要明顯減少.進一步觀察發現，在這些長釘一般豎線之間，都有幾段很小的區域幾乎貼著橫軸，且以天為周期出現，這是每天早晨銀行開門時客戶集中點擊叫號機打印小票的結果，并且只維持較短的時間.由此可以判斷，銀行客戶到訪會在很長時間都沒有發生，也會有在短時間內陣發.

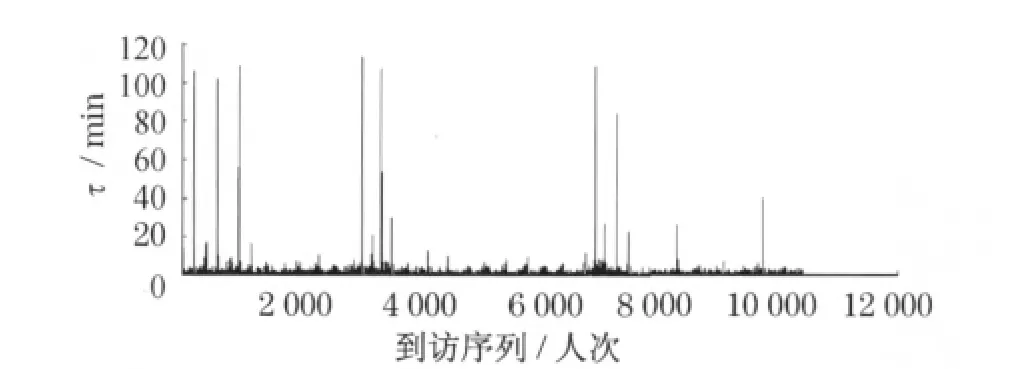
圖2 19天內所有客戶到訪間隔時間Fig.2 Inter－arrival time of total customers in 19days

2 客戶到訪行為的統計特征

銀行業務是現代社會易于獲取的服務，每個人都會隔一段時間訪問銀行.不同的人，訪問銀行的相隔時間會有不同的差異，有的人一天會訪問好多次，有的人很長一段時間內都不會親自訪問銀行.根據上文分析，一個網點接受該地區客戶訪問單位時間內的客戶數量會有很大的漲落，類似情況也發生在客戶到訪的間隔時間上，有的時段一個客戶也沒有，而有的時段幾秒鐘就有一個客戶到訪.這些現象再次說明，人類的行為并不能被認為是一種泊松過程，而是大部分不同客戶之間都有著某種共同的特性，經過研究，發現這種特性與泊松分布有很大的差異.本文將一段時間內所有客戶或同一類型客戶看成一個整體，考察客戶到訪銀行的間隔時間統計特征，從而獲得該網點客戶訪問銀行的總體行為特征.

2.1 所有客戶到訪間隔時間分布

統計結果顯示，銀行客戶到訪的間隔時間分布滿足P（τ）∝τ－α（α為冪指數），冪指數約為3，如圖3所示.客戶訪問量的高峰一般出現在10：00～11：00、13：00～14：00點之間，訪問量的低峰出現在12：00～13：00、16：00～17：00之間，這主要和該網點員工的工作時間與休息時間有關.大部分的客戶到訪間隔時間較短，像周末中午時間段出現很長的到訪間隔時間是很少的，正是時間間隔的不均勻性造成了冪律分布的形成.

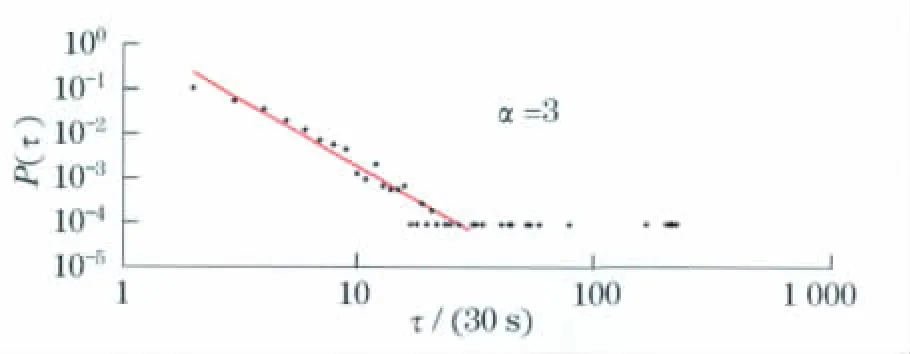
圖3 雙對數坐標下所有銀行客戶到訪的間隔時間分布Fig.3 Inter－arrival distribution of bank customers visiting in 19days under double logarithmic coordinates

2.2 單日客戶到訪的間隔時間分布

圖4是某個休息日和某個工作日客戶到訪的間隔時間分布.統計結果顯示，客戶到訪的間隔時間分布也符合冪律分布，而冪指數分別約為2.45和2.5.該休息日的客戶訪問量為417人次，其中個人業務392人次，公司業務3人次，其它22人次；該工作日的客戶訪問量為620人次，其中個人業務364人次，公司業務203人次，其它53人次.而休息日客戶到訪平均間隔時間為69s，工作日客戶到訪平均間隔時間為47s.休息日最大到訪間隔時間為6 060s，工作日最大到訪間隔時間為597s，兩天最小到訪間隔時間皆為1s.客戶訪問量、客戶結構、客戶到訪平均間隔時間等都有較大差異，而冪指數十分相近.接著計算數據庫中每一天的客戶到訪間隔時間分布，發現都近似服從冪律分布，而冪指數范圍為2.3～2.5之間.休息日與工作日的冪指數并沒有較大差異，這表明銀行客戶到訪有著共同的特性，而且對于休息日、工作日并無差別，形成這種特性的機制還尚不清楚.

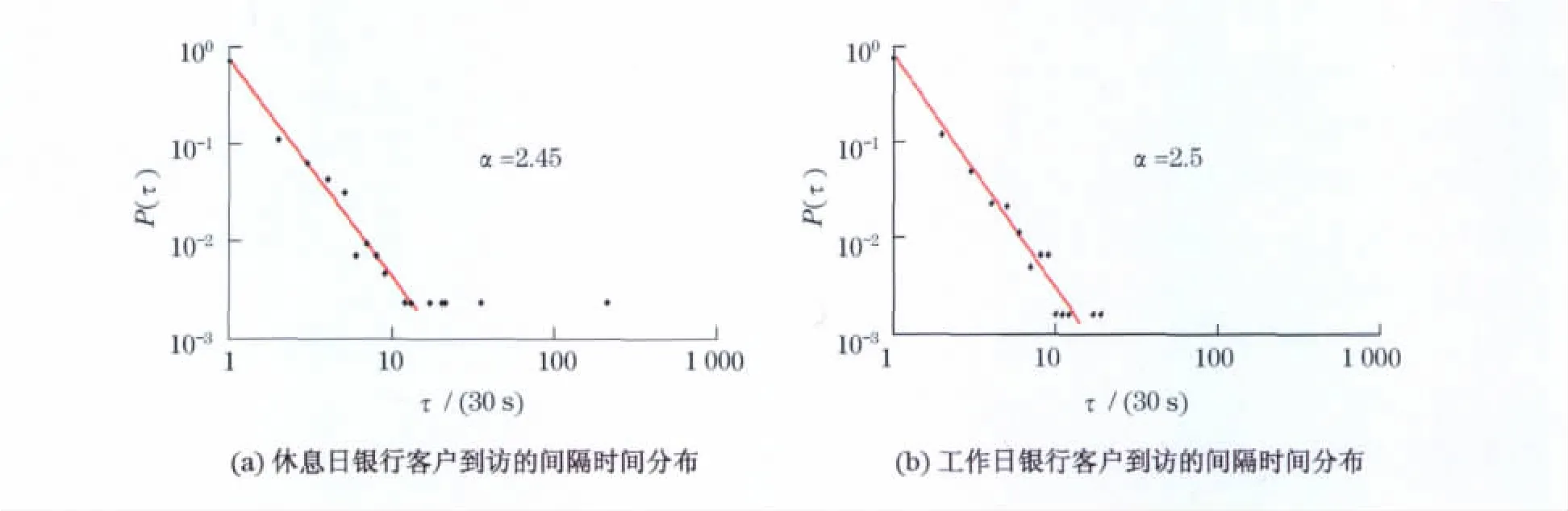
圖4 某個休息日和某個工作日客戶到訪的間隔時間分布Fig.4 Inter－arrival distributions of bank customers visiting on an off day and on a working day

3 細分客戶到訪行為的統計特征

銀行個人業務和公司業務具有很大的差別，那么個人業務客戶和公司業務客戶前往銀行辦理業務的行為是否還會保持著某種特有的性質，接下來本文分析細分客戶到訪行為的分布情況，見圖5.由于數據量的關系無法對其它業務進行合理的分析，待今后能得到更多相關數據時再次討論.細分客戶到訪的間隔時間分布是一種特定客戶的分析（用戶都是某銀行網點的客戶），每一類型的客戶訪問銀行都受到很多因素的影響，例如工作時間、休息時間等.所以，可能和其他類型客戶訪問銀行的情況在冪指數上存在一定的偏差，如退休職工辦理個人業務時對于工作日或者休息日的選擇并沒有差異，而公司業務一般是在工作日前往銀行辦理，這種分析反映了社會某一個層面的人類活動特性.

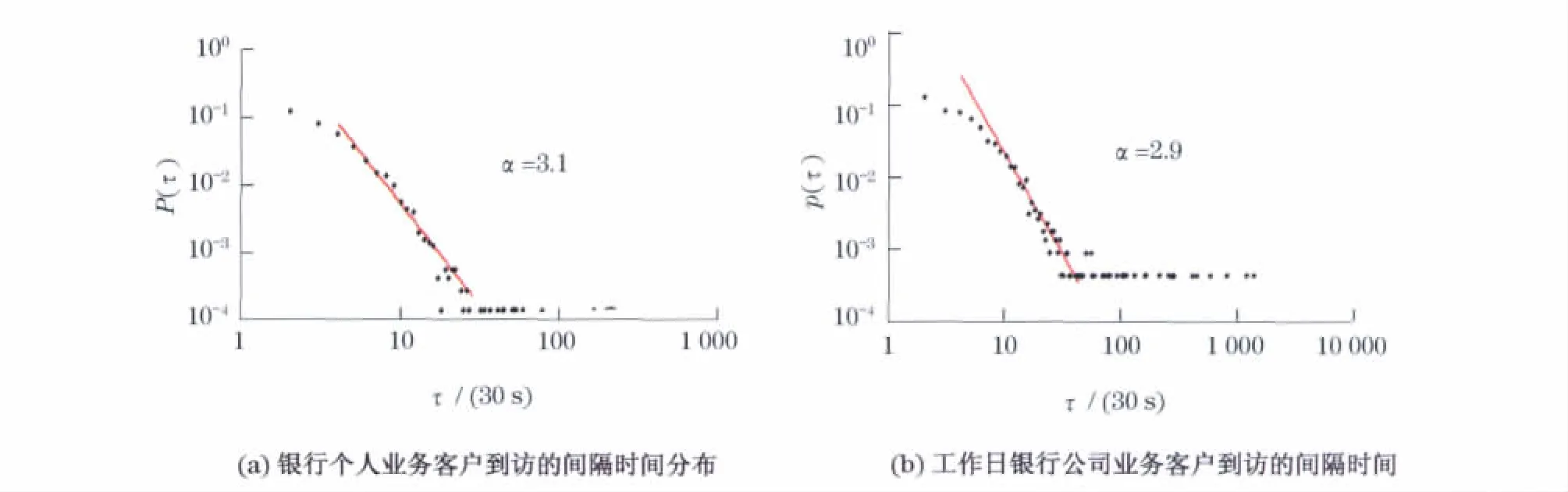
圖5 19天內銀行細分客戶到訪的間隔時間分布Fig.5 Inter－arrival distributions of customers visiting for personal banking business and for corporate banking business in 19days

統計結果顯示，個人業務客戶到訪的間隔時間分布服從冪律分布，冪指數約為3.1.公司業務客戶到訪的間隔時間分布服從冪律分布，冪指數約為2.9.這種差異可以從個人業務和公司業務的特點上解釋.個人業務在總的業務量上占了約70%，銀行開門后密集訪問的客戶群和銀行當日歇業前最后一個客戶都是個人業務客戶，正是個人業務客戶到訪時間間隔的不均勻性使間隔時間分布出現了冪律.圖6給出的個人業務客戶到訪間隔時間圖，可以發現個人業務客戶的間隔時間圖與所有客戶的間隔時間圖的形狀十分相似.那些長釘一般的豎線是由于個人業務客戶在周末中午到訪間隔時間較大造成的，這些豎線與圖2中長釘般豎線的長度及出現的位置基本一致.而公司員工一般集中在工作日前往銀行辦理業務，很少會在休息日處理，除非有緊急事務，因此每逢周末都會出現相比個人業務客戶更長的間隔時間（見圖7）.正是由于個人業務客戶和公司業務客戶到訪時間間隔的極不均勻性形成了冪律.

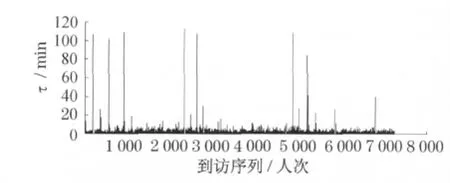
圖6 19天內個人業務客戶到訪間隔時間Fig.6 Inter－arrival time of customers visiting for personal banking business in 19days

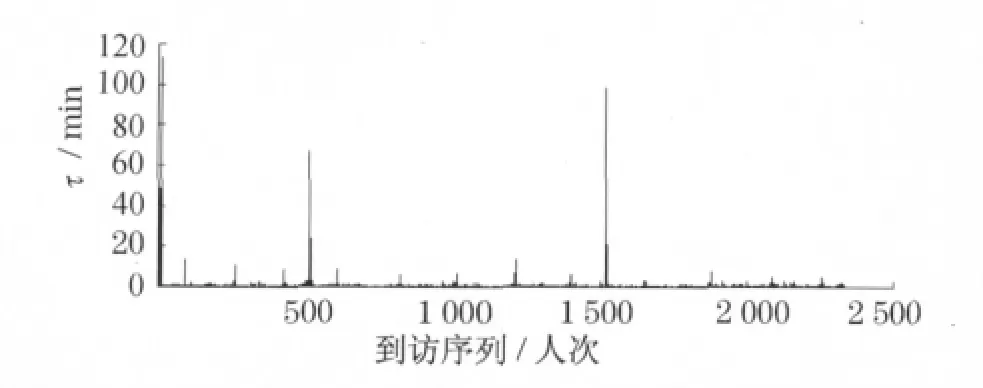
圖7 19天內公司業務客戶到訪間隔時間Fig.7 Inter－arrival time of customers visiting for corporate banking business in 19days

4 小 結

本文主要討論銀行客戶的到訪行為模式和個人業務客戶、公司業務客戶到訪的間隔時間分布的統計特性.由分析結果可以得出銀行客戶到訪的間隔時間分布、單日銀行客戶到訪間隔時間分布、個人業務客戶到訪間隔時間分布、公司業務客戶到訪間隔分布都是滿足P（τ）∝τ－α（α在2到3之間）的冪律分布.因此，有理由認為銀行客戶到訪的時間間隔分布具有冪律特性.統計結果再次說明人類行為可能在很多個層面上都偏離泊松過程.這個發現為排隊理論的創新奠定了實證基礎，具有一定的意義，同時也為解決銀行排隊擁擠問題奠定了理論基礎.就排隊論視角而言，銀行排隊問題還牽涉客戶等待時間、服務時間、隊長等，后續工作將對這些問題進行研究.進而，將實證某高校財務事務排隊系統和研究統計的時間單位對排隊指標分布形狀的影響.

［1］ 曹杰.行為科學［M］.北京：科學技術文獻出版社，1987.

［2］ 李楠楠，周濤，張寧.人類動力學基本概念與實證分析［J］.復雜系統與復雜性科學，2008，5（2）：15－24.

［3］ Haight F A.Handbook of the Poisson distribution［M］.New York：Wiley，1967.

［4］ Barabási A L.The origin of bursts and heavy tails in human dynamics［J］.Nature，2005，435（7039）：207－211.

［5］ 郭進利.博客評論的人類行為動力學實證研究和建模［J］.計算機應用研究，2011，28（4）：1422－1424.

［6］ 李楠楠，張寧，周濤.人類通信模式中基于時間統計的實證研究［J］.復雜系統與復雜性科學，2008，5（3）：43－47.

［7］ 樊超，郭進利.基于圖書借閱的人類行為標度律分析［J］.圖書情報工作，2010，54（1）：35－39.

［8］ 顏薇娜.基于蒙特卡洛模擬的商業銀行排隊問題研究［J］.技術經濟與管理，2009（1）：20－22.

［9］ 楊米沙.銀行排隊系統數據分析及窗口設置優化研究［J］.武漢理工大學學報（信息與管理工程版），2008，30（4）：20－22.