基于蒙特卡羅方法的矩形布局問題研究

2012-03-21 05:33:08鄭榮杰張鵬程崔海良李國順羅海兵劉昕彤

圖學學報 2012年4期

關鍵詞：方法

鄭榮杰，張鵬程，崔海良，李國順，羅海兵，劉昕彤

（河北工程技術高等專科學校，河北滄州 061001）

矩形布局[1]是在矩形的邊與布局空間邊界平行的情況下，將其不相嵌地放入布局空間中，同時達到空間排布的最優化。這一問題屬于布局問題的一個子問題。它在機械設計與制造、交通運輸、大規模集成電路設計等領域有著廣泛的應用，是當前CAD/CAM研究的熱點問題之一[2]。

布局問題作為具有NP-hard的最優組合問題，在有限的時間內一般無法獲得全局最優解[3]。對其求解只能依賴于各種啟發算法，其中構造式啟發方法應用最廣[4]。使用構造式方法求解矩形布局，其過程分為定序和定位兩步:定序規則確定矩形布入的次序，定位規則確定矩形布入位置。矩形可行域是指待布矩形在布局空間中所有可行位置的集合。近來，研究發現結合矩形可行域制定定序規則和定位規則，可以使矩形布局過程更靈活，算法的自適應性更強[4]。

隨著矩形布入，布局空間的邊界發生變化，邊界的形狀變得復雜。確定此類空間中矩形可行域成為一個難題。考慮到蒙特卡羅方法研究非確定性問題的優勢[5]，我們將其引入到于矩形可行域研究，最終得到了有意義的結果。

1 蒙特卡羅方法

蒙特卡羅方法[6]，是一種根據統計抽樣理論近似求解數學物理問題的計算機模擬方法，已廣泛應用于金融工程學，宏觀經濟學，生物醫學，計算物理學等領域。對于確定性問題，其基本思想是：建立一個與所求解有關的概率模型，基于這個模型進行隨機抽樣；通過對隨機抽樣進行統計，得到概率模型的分布或數學期望作為近似解。對于非確定性問題，蒙特卡羅方法則無需將非確定性問題轉化為確定問題再求解，而是直接從非確定性問題出發，通過模擬問題的實際過程得到問題的解。考慮到布局問題具有非確定性,采用蒙特卡羅方法對矩形布局過程進行直接模擬，可以獲得一種有效的布局方案。

2 矩形可行域

矩形可行域是指矩形在布局空間中所有可行位置的集合。在規則的布局空間中，矩形的可行域為矩形沿布局空間邊界移動時，矩形的中心形成的封閉軌跡占據的區域。如圖1所示，長為2，寬為1的矩形在邊長為5的正方形中沿邊界移動，得到多邊形占據的區域即為矩形可行域。

圖1 正方形布局空間中矩形的可行域

隨著矩形布入，剩余布局空間的邊界發生變化，成為不規則的布局空間。對于此類布局空間，可行域不能由矩形沿著空間邊界移動直接得到。如圖2所示，在布局空間左下角布入一個矩形后，下一個矩形在沿剩余布局空間邊界移動時，位于位置1時滿足邊界條件；位置2時，則不符合。

如何得到不規則布局空間中符合邊界條件的可行域是計算可行域的難點。王金敏等提出偏移多邊形法，利用布局空間頂點的坐標及布局矩形的尺寸關系進行比較得到矩形可行域的邊界[7]。此方法較好的解決了這一問題，但在計算可行域邊界時，算法較為復雜。本文使用蒙特卡羅方法控制矩形在布局空間中移動，由邊界條件限制矩形布局的范圍，可行域的邊界自動滿足布局空間邊界條件，簡化了可行域邊界的確定過程。

圖2 剩余布局空間中矩形的可行域

3 矩形可行域求解算法及步驟

使用蒙特卡羅方法確定矩形可行域的步驟如下：

1）將布局空間劃分成若干個格子。

2）確定矩形在布局空間的初始分布。依次在布局空間的頂點上設置滿足邊界約束條件的矩形，使得矩形可以到達布局空間的任何區域。

3）布局空間中，矩形按照蒙特卡羅法得到的隨機步長沿水平或垂直方向做試探移動；同時矩形的移動需滿足布局空間的邊界條件。

4）統計滿足布局空間邊界條件的矩形中心分布位置。

5）根據矩形中心的分布位置得到矩形可行域。

下面給出了不規則布局空間中矩形可行域的求解實例。如圖3所示，布局空間是一個不規則多邊形，在x軸上位于區間[0,20]，y軸上位于區間[0,16]內。待布矩形是長為4，寬為2的矩形。為了保證矩形可以到達布局空間的任何位置，矩形在布局空間中初始位置需要滿足條件：矩形至少有一條邊和一個頂點分別與不規則多邊形的邊和頂點重合，并且位于布局空間內。如圖2中所示，虛線構成的陰影矩形作為矩形的初始位置。

圖3 不規則布局空間及矩形的一些初始分布位置

矩形按照蒙特卡羅方法產生的隨機步長在布局空間中沿水平或垂直方向試探移動。如果矩形在試探移動后，仍位于布局空間內，則記錄此時矩形中心的位置；否則不記錄，做下一次試探移動。統計矩形的中心在布局空間中分布區域，即得到如圖4所示的矩形可行域。圖4中的點、直線以及閉合曲線占據的區域即為矩形可行域。其中，點表示此處只存在一種矩形的放置方式；直線表示矩形的中心可以沿著此直線運動。圖中閉合曲線圍住的區域表示矩形中心可在此區域內運動。

圖4 矩形在布局空間中的可行域

顯然，通過蒙特卡羅方法移動的矩形，自動滿足布局空間的邊界條件；得到的可行域邊界必然同樣符合布局空間邊界約束。該方法在模型及算法上較傳統方法更為直觀，簡單。

4 實例分析

利用蒙特卡羅方法確定矩形可行域，采用王金敏提出的定位函數及吸引子方法進行矩形的定位，從而完成矩形的布局過程[4]。定位函數的具體形式為

采用java語言完成了自動布局系統的設計。在Pentium(R) Dual-Core (2G/2.5GHz)微機上，測試了 http://people.brunel.ac.uk/～mastjjb/jeb/orlib/files/strip3.xls下載的實例數據，驗證了本算法的有效性。在圖5中，給出了strip3.xls文件的T1表中兩例17個矩形在布局空間中的典型測試結果。圖6為矩形占據布局空間的比例隨著布入矩形數的變化規律。在實例1中矩形最終占據布局面積比例為91.653%，實例2中為91.368%。結果顯示，使用蒙特卡羅方法得到的矩形可行域，應用于矩形布局時，可以達到較好的布局效果。

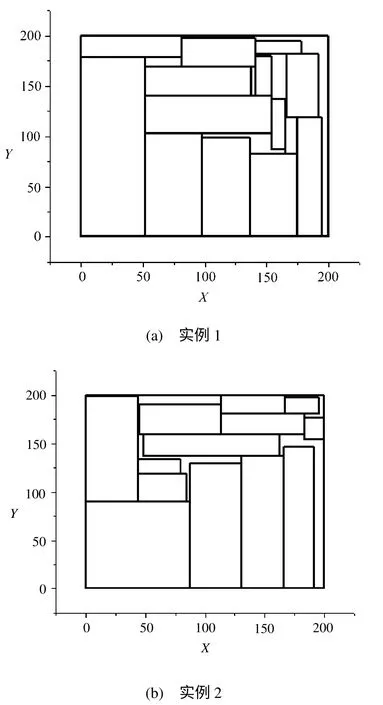
圖5 實例中矩形的布局結果

圖6 矩形占據布局空間比例與布入矩形數的關系

5 結論

本文基于蒙特卡羅方法研究矩形布局問題。使用蒙特卡羅方法控制矩形在布局空間中移動，由邊界條件限制矩形布局的范圍，得到的可行域邊界自動滿足布局空間邊界約束。結合定位函數,最終獲得了良好的布局結果。該方法很大程度上簡化了可行域邊界的確定過程，最終提高了布局算法的效率。

使用蒙特卡羅方法確定矩形的可行域，計算過程只受布局空間邊界約束，與待布矩形的形狀和位置無關，所以在確定邊界條件的前提下，該方法可擴展應用于矩形、三角形和圓形的混合布局問題。

[1]Dowsland K A, Dowsland W B. Packing problem [J].European Journal of Operational Research, 1992,56(1): 2-14.

[2]Sweeney P W, Paternoster E R. Cutting and packing problem: a categorized application-orientated research [J]. Journal of Operation Research Socity,1992, 43(7): 691-706.

[3]王金敏, 喻宏波, 陳東祥, 等. 布局模裝系統的研究[J].工程圖學學報, 2001, (1): 47-54.

[4]王金敏, 楊維嘉. 動態吸引子在布局求解中的應用[J].計算機輔助設計與圖形學學報, 2005, 17(8):1725-1730.

[5]馬海云, 齊小軍. 蒙特卡羅仿真機及其應用[J]. 電腦與信息技術, 2006, 14(3): 8-10.

[6]Metropolis N, Rosenbluth A W, Rosenbluth M N, et al.Equation of state calculations by fast computing machines [J]. J. Chem. Phys, 1953, 21: 1087.