一種基于Kd-tree 射線追蹤法的衛(wèi)星RCS 預(yù)估方法

肇 格,張 軍,胡杰民

(國防科技大學(xué)ATR國防科技重點實驗室,長沙410073)

1 引 言

低頻方法在雷達(dá)散射截面(RCS)的計算上有著很大的局限性,特別是對于電大尺寸具有復(fù)雜結(jié)構(gòu)的目標(biāo),該方法往往是行不通的。而對于普通的高頻方法,例如物理光學(xué)方法,由于其是建立在很多種近似上的,所以在計算很多問題時很難達(dá)到準(zhǔn)確性的要求。射線追蹤與物理光學(xué)(PO)相結(jié)合的方法包含了散射場中多次散射的高階項,是計算具有多次散射效應(yīng)目標(biāo)RCS 的一種有效方法,其有效性已經(jīng)得到了大量的驗證[1-3]。但這種方法也只被用在了角反射器的計算上。

根據(jù)衛(wèi)星目標(biāo)的三維面元模型建立起來的Kd-tree 是一種根據(jù)k 維空間中的點集對空間進(jìn)行分割的數(shù)據(jù)結(jié)構(gòu),常用于范圍查找和最近鄰查找等,是一種特殊的二叉空間分割樹[4-5]。文獻(xiàn)[5]中作者將其用于射線追蹤方法使得對于射線的追蹤效率大大提高。本文將Kd-tree 方法應(yīng)用于射線追蹤,仿真結(jié)果表明該方法在計算效率方面達(dá)到了良好的效果,結(jié)合PO 方法就可以得到給定模型的RCS 預(yù)估值。計算結(jié)果表明,結(jié)合了Kd-tree 和射線追蹤的方法可以有效地計算復(fù)雜電大尺寸空間目標(biāo)的RCS預(yù)估值。

2 衛(wèi)星目標(biāo)模型的剖分原則

衛(wèi)星目標(biāo)模型建好之后,將其剖分成小的三角面元,具體的剖分應(yīng)當(dāng)遵循以下原則:假定每個小面元都只有被照射和未被照射兩種情況。因此,為了比較準(zhǔn)確地反映多次散射的情況,剖分時每個面元都不能太大,以使最小結(jié)構(gòu)都能被面元模型很好地描述。在滿足上述條件下,為了提高計算精度,這里采用九點插值方法對每一面元的物理光學(xué)積分進(jìn)行計算。

3 Kd-tree 結(jié)構(gòu)的建立

Kd-tree 結(jié)構(gòu)是自上而下以一種遞歸的方式構(gòu)造的,其中根節(jié)點對應(yīng)于包含了目標(biāo)所有面元的長方體包圍盒。然后長方體包圍盒按一個軸方向被分割平面分成兩個子長方體,組織成一個二叉樹,即一個根節(jié)點被分成了兩個內(nèi)節(jié)點。剖分平面是選擇使射線與面元相交概率最大的平面,且該平面可以是垂直于x 、y 、z 軸的任何一個平面。若某一子長方體包圍盒中所含的面元數(shù)大于給定的值,且Kd -tree 的深度小于給定的深度,則需對該子包圍盒進(jìn)一步剖分。上述剖分過程遞歸地進(jìn)行,直至Kd -tree 的每一個葉子節(jié)點所對應(yīng)的子空間所包含的面元數(shù)小于給定的值或該Kd-tree 的深度大于給定的深度為止。另外,如果分割過程中面元與分割平面相交,則使面元分別屬于兩個相應(yīng)的節(jié)點。Kd-tree建立之后,還需使每一葉子節(jié)點對應(yīng)的包圍盒的6個面與其他內(nèi)節(jié)點,葉子節(jié)點或空節(jié)點建立指向關(guān)系,具體細(xì)節(jié)可以參見文獻(xiàn)[4] 。Kd-tree 的建立可以大大減小反射線追蹤時從Kd-tree 自上而下的追蹤過程。二維的Kd-tree 如圖1 所示。

圖1 二維Kd-tree 模型Fig.1 The two-dimensional model of Kd-tree

4 PO 積分與路徑的射線追蹤

4.1 應(yīng)用物理光學(xué)積分計算每一面元一階等效電流對于遠(yuǎn)區(qū)散射場的貢獻(xiàn)

本文所介紹的方法是以面元為單位進(jìn)行的,即計算出每一面元各階等效電流對于遠(yuǎn)區(qū)散射場的貢獻(xiàn),然后將所有面元的貢獻(xiàn)相加即可得總的遠(yuǎn)區(qū)散射場。其中,每一面元對于遠(yuǎn)區(qū)散射場的貢獻(xiàn)可用物理光學(xué)積分表示為

其中,Hsm為面元m 對于遠(yuǎn)區(qū)散射場的貢獻(xiàn),Jm1、Jm2等為面元m 上的一階、二階和更高階電流。

應(yīng)用切平面近似,面元m 上的一階等效電流可表示為

其中, m 為面元m 的法向矢量, Hi為面元m 處的磁場強度。

4.2 根據(jù)入射波判斷初次入射明暗面

該步驟需對所有面元一一進(jìn)行判斷,判斷其是否被入射波直接照射到。判斷某一面元m 是否被入射波照射到的方法如下。

設(shè)入射波矢量為 i,面元m 的法向矢量為 n ,則m 面元被入射波照亮應(yīng)滿足以下兩個條件:

(1)入射波矢量為 i 與面元m 的法向矢量為 m(mx,my,mz)滿足: i × m ≤0;

(2)入射波照射到面元m 的過程未被其他面元遮擋。

其中,條件2 的判斷方法如下:

設(shè)面元中心點坐標(biāo)rm(xm, ym,zm),入射波矢量 i(ix,iy,iz),該面元上的入射線方程為

將該直線方程與其他面元逐一進(jìn)行判斷,如果該直線方程與其他所有面元無交點,則面元m 未被其他面元遮擋,即面元m 被入射波直接照射到,否則面元m 在入射波照射過程被其他面元遮擋,未被入射波直接照射到。

以面元n 為例,判斷式(3)直線與面元n 是否有交點的方法如下。

設(shè)面元n 的中心點坐標(biāo)為rn(xn, yn,zn),面元法向矢量為 n(nx, ny,nz),則該面元所在的平面可表示為

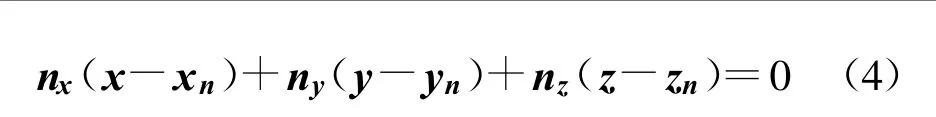
聯(lián)立式(3)與式(4)可求得式(3)直線與面元n所在平面的交點P(x0,y0,z0)。這里:

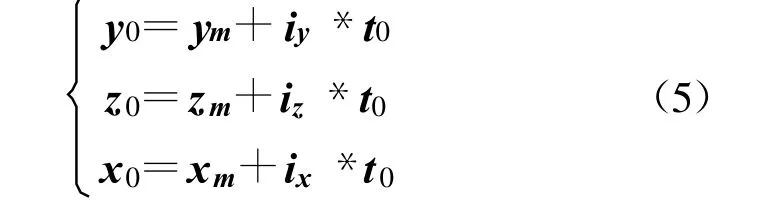
其中:

t0=[ nx(xn-xm)+ny(yn-ym)+nz(zn-zm)]/[ nx·ix +ny·i y+nz·iz] 。

因為我們判斷的是射線到達(dá)面元m 之前的情況,所以t 0應(yīng)該小于0。此時,如果該交點P(x0,y0,z0)在面元n 內(nèi),則式(3)與面元n 有交點,否則式(3)與面元n 無交點。判斷一點P(x0, y0,z0)是否在三角形面元n 內(nèi)的方法如下:

3 個頂點N1、N2、N3與面元n 的法向矢量n (nx,ny,nz)成右手螺旋法則的順序排列,如圖2 所示,則P 點位于面元n 內(nèi)部的充要條件是式(6)中的3 個式同時滿足。

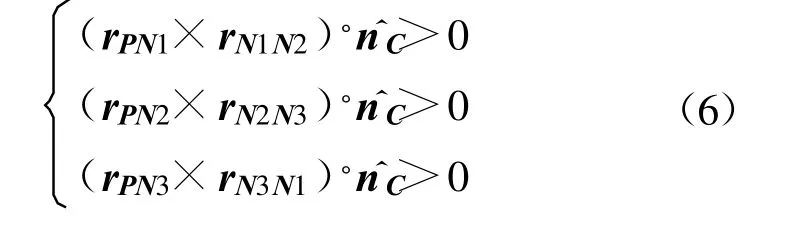
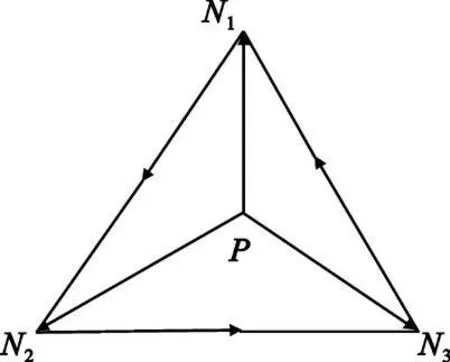
圖2 射線與面元相交判斷Fig.2 Intersect judge of ray and surface

4.3 面元處二階等效電流對遠(yuǎn)區(qū)散射場的貢獻(xiàn)的計算

仍以經(jīng)面元n 反射的反射線照亮面元m 為例。面元n 處的入射場可表示為

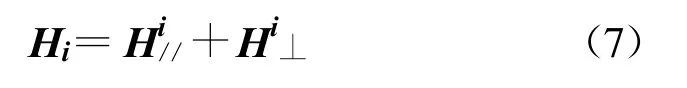
則經(jīng)面元n 反射的反射場可表示為

其中,Hi// = e//·Hi,Hi⊥= e ⊥·Hi, e ⊥= i × n, e// = i× e⊥, er//= k × e⊥, Γ//和Γ⊥分別為平行極化和垂直極化的反射系數(shù)。

5 仿真結(jié)果

算例1:三面角反射器是驗證高頻多次彈跳散射的標(biāo)準(zhǔn)[6]。這里所取的三面角反射器中直角三角形的直角邊長為1 m,如圖3 所示。θ在φ=45°的平面從0°到90°變化,入射波頻率為6 GHz,VV 極化。

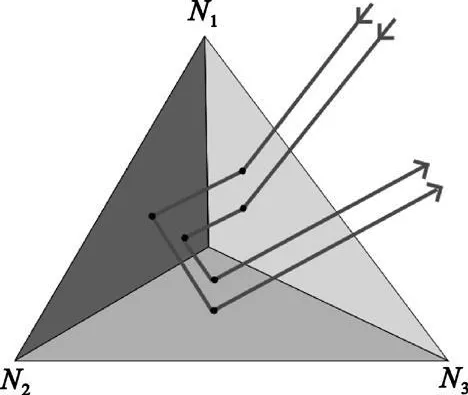
圖3 三面角反射器Fig.3 Three sides of corner reflectors

圖4 給出了三面角反射器的后向散射系數(shù),并將其與MoM 方法的結(jié)果進(jìn)行了比較。從圖中可以看出,本文所提出的方法與MoM 方法所得的結(jié)果符合得很好。在計算效率方面,MoM 方法耗時超過24 h,而本文所提出的方法計算所有90 個角度用時5 min。

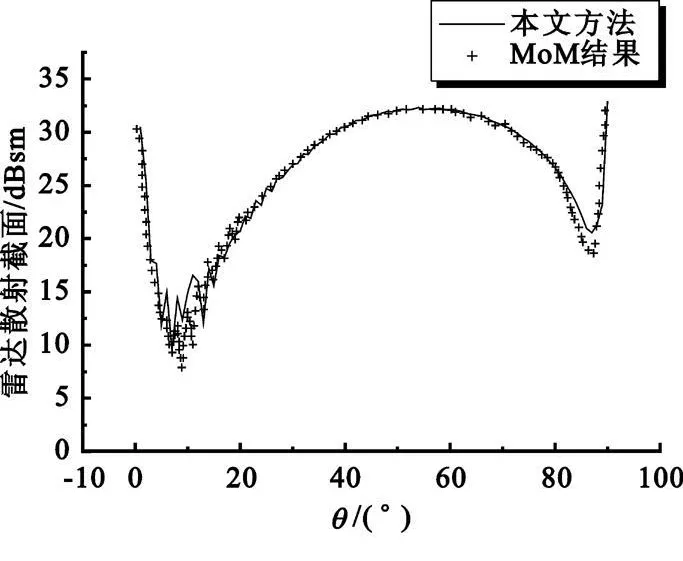
圖4 本文方法與MoM 方法結(jié)果比較Fig.4 Comparison between the proposed method and the MoM

算例2:將該方法應(yīng)用于衛(wèi)星目標(biāo)的計算。衛(wèi)星模型如圖5 所示,在模型上面的平臺上為一天線面結(jié)構(gòu),該天線面結(jié)構(gòu)中有圓柱和方體結(jié)構(gòu),模型被剖分為29 569個面元。入射波頻率為3 GHz,VV 極化。

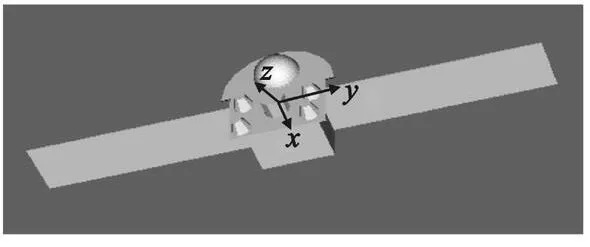
圖5 衛(wèi)星模型Fig.5 Satellite model

圖6 給出了本文方法所得結(jié)果與實驗結(jié)果和單純PO 方法所得結(jié)果的比較。從圖中我們可以看出,單純的PO 方法結(jié)果與實驗結(jié)果相差很大,這表明對于衛(wèi)星天線面這種復(fù)雜結(jié)構(gòu),各部分之間多次散射的效應(yīng)十分明顯,而單純的PO 方法未能包含這種效應(yīng)。本文的改進(jìn)方法則能有效涵蓋這種多次散射效應(yīng),所以與實驗結(jié)果符合得比較好。

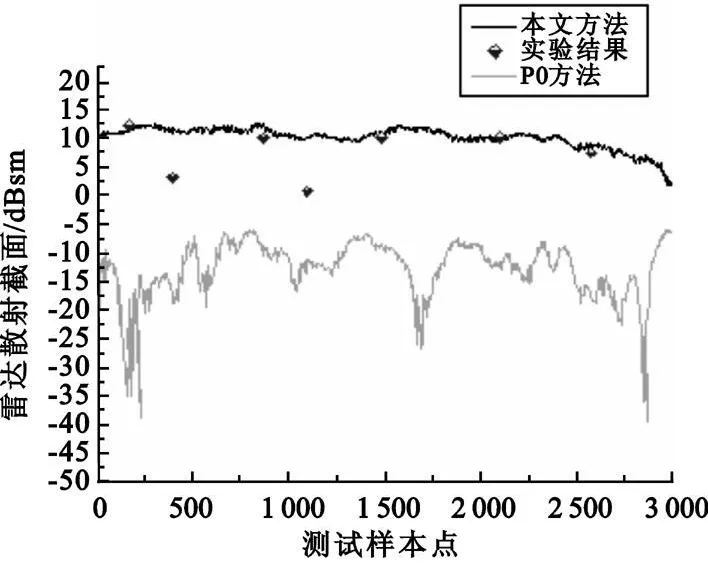
圖6 衛(wèi)星RCS 計算結(jié)果比較Fig.6 Comparison of satellite RCS calculation

6 結(jié) 論

本文提供了一種將PO 方法與Kd-tree 空間分割方法及射線追蹤相結(jié)合的改進(jìn)方法。該方法因為有效地計入了目標(biāo)各部分之間的多次散射效應(yīng),且為一種高頻方法,所以對于計算電大尺寸具有較強耦合效應(yīng)的復(fù)雜目標(biāo)是非常行之有效的。為了方便起見,本文沒有考慮邊緣繞射效應(yīng)所產(chǎn)生的影響,如果用物理繞射理論(PTD)對之加以修正,可能會得到更令人滿意的結(jié)果。值得一提的是,其他大多數(shù)方法的計算量會隨著入射波頻率的增大而顯著增加,而本文方法的計算量則不會受到入射波頻率的影響,這使得該方法在高頻散射計算時更能顯示出更多的優(yōu)勢。

[1] Knott E F.RCS reduction of dihedral corners[ J] .IEEE Transactions on Antennas and Propagation,1977, 25(3):406-409.

[2] Ross R A.Application of geometrical diffraction theory to reflex scattering centers[C]//Proceedings of 1968 IEEE International Symposium on Antennas and Propagation.Monterey,CA:IEEE,1968:94-99.

[3] Anderson W C.Consequence of nonorthogonality on the scattering properties of dihedral reflectors[ J] .IEEE Transactions on Antennas and Propagation, 1987,35(10):1154-1159.

[4] Havran V.Heuristic Ray Shooting Algorithm[D] .Prague:University Czech Technical, 2000.

[5] Tao Y B, Lin H, Bao H J.Kd-tree based fast ray tracing for RCS prediction[ J] .Progress in Electromagnetics Research, 2008, 81:329-341.

[6] Baldauf J, Lee S W, Lin L, et al.High frequency scattering from trihedral corner reflectors and other benchmark targets:SBR vs.experiments[ J] .IEEE Transactions on Antennas and Propagation, 1991,39(9):1345-1351.

[7] Tao Y B, Lin H, Bao H J.GPU-based shooting and bouncing ray method for fast RCS prediction[J] .IEEE Transactions on Antennas and Propagation,2010,58(2):494-502.