非均勻內水壓力作用下的壩下箱涵結構計算

蔡勇斌，劉月琴，蔡勇平，蔡曉鴻

（1.江西省吉安市水利局，江西吉安343000；2.江西省吉安市水利水電規劃設計院，江西吉安343000）

0 引言

箱涵是壩下涵管常見結構型式之一，壩下箱涵受土壓力作用的內力與變位計算已有成熟的結構力學解法[1]，但壩下箱涵受非均勻內水壓力作用，特別是側墻受梯形荷載作用的內力與變位計算卻鮮見介紹。本文依據彈性地基梁理論，將箱涵底板與頂板分別視為承受內水壓力P1、P2作用的固端彈性地基梁，將箱涵側墻視為底端承受內水壓力P1、頂端承受內水壓力P2梯形分布荷載作用的固端彈性地基梁，采用左手坐標系，按彈性地基梁初參數法與地下框架結構位移法彎矩與剪力正、負號匹配關系，建立了箱涵底板、頂板、側墻載常數計算方法，給出了箱涵受非均勻內水壓力作用時的內力與變位解析計算式。

1 壩下箱涵載常數

1.1 箱涵底板載常數

壩下箱涵底板可簡化為受均布內水壓力P1作用的兩端固定彈性地基梁，采用左手直角坐標系，其計算簡圖見圖1。

圖1 壩下箱涵底板載常數計算簡圖Fig.1 Calculation diagram of load constants of the bottom plate

由彈性地基梁受均布荷載P1作用下的初參數變位解，且注意到箱涵底板左端A為初始截面，桿端彎矩MˉAB、MˉBA以順時針方向為正，桿端剪力以指向地基方向（沿y軸方向）為正，于是箱涵底板撓度計算式為

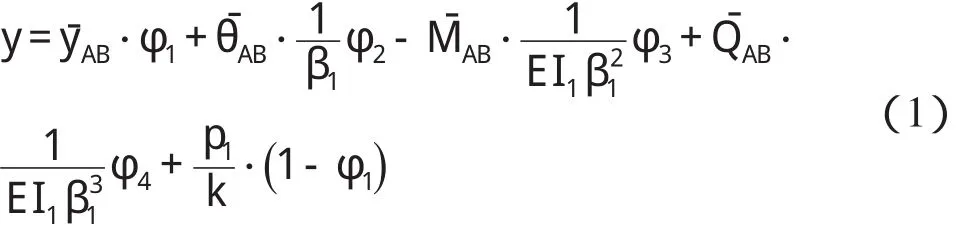
β1為壩下箱涵底板特征系數k為壩下箱涵彈性抗力系數，若不計地基彈性抗力，則在計算時k可取很小值；E為壩下箱涵混凝土彈性模量；I1為壩下箱涵底板截面慣性矩。

據箱涵底板載常數計算簡圖，由左端邊界條件y|x=0==0，θ|x=0==0，據式（1）可得底板撓度方程、轉角方程、彎矩方程及剪力方程。

又利用底板右端邊界條件y|x=l==0，θ|x=l==0，據式（2）、式（3）可得底板左端及右端載常數。

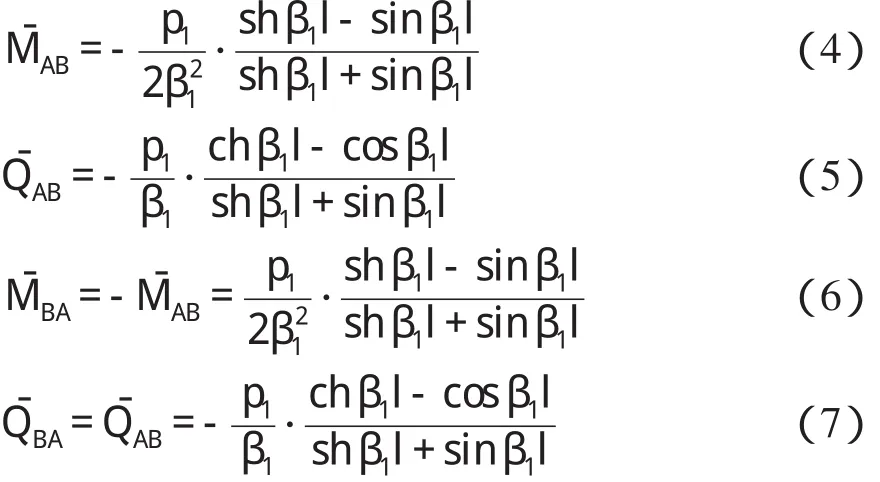
1.2 箱涵頂板載常數

壩下箱涵頂板可簡化為受均布內水壓力p2作用的兩端固定彈性地基梁，計算簡圖如圖2。

圖2 壩下箱涵頂板載常數計算簡圖Fig.2 Calculation diagram of load constants of the roof

類似于壩下箱涵底板載常數的推導，且注意到箱涵頂板所受均布內水壓力p2作用方向垂直向上，可得箱涵頂板左、右固端載常數分別為：

式中，為壩下箱涵頂板特征系數；I2為箱涵頂板截面慣性矩；其余符號意義同前。

1.3 箱涵左側墻載常數

壩下箱涵左側墻為受向左方向作用的內水壓力梯形荷載兩端固定彈性地基梁，其計算簡圖如圖3所示。

圖3 壩下箱涵左側墻計算簡圖Fig.3 Calculation diagram of the left side wall of the box cul?vert beneath dam

由彈性地基梁受梯形荷載作用下的初參數變位解，且注意到剪力以指向地基方向為正，于是有箱涵左側墻撓度計算式

由箱涵側墻頂端邊界條件y|x=0==0；θ|x=0==0，可得箱涵側墻撓變方程、轉角方程、彎矩方程及剪力方程：

利用箱涵左側墻底端邊界條件y|x=h==0；θ|x=h==0，據式（11）、（12），可得箱涵左側墻頂端及底端載常數：

1.4 箱涵右側墻載常數

壩下箱涵右側墻為受向右方向作用的梯形內水壓力荷載兩端固定彈性地基梁，其計算簡圖如圖4所示。

圖4 壩下箱涵右側墻計算簡圖Fig.4 Calculation diagram of the right side wall of the box cul?vert beneath dam

類似于壩下箱涵左側墻載常數的推導，據對稱性，可得箱涵右側墻頂端及底端載常數為

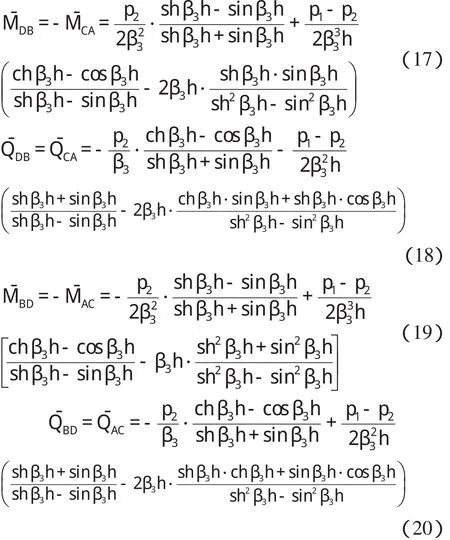
2 壩下箱涵形常數

據如下彈性地基梁無載段撓度方程、轉角方程、彎矩方程與剪力方程式

可推導出如下彈性地基梁兩端轉動形常數與移動形常數（圖5）

式中：sh、ch、sin、cos分別為sh βl、ch βl、sin βl、cosβl的簡寫。

S為梁端發生單位轉角時的本端彎矩；S′為梁端發生單位轉角時的遠端彎矩；

J為梁端發生單位移動時的本端剪力；J′為梁端發生單位移動時的遠端剪力；

T為梁端發生單位轉角時的本端剪力，或梁端發生單位移動時的本端彎矩；

T′為梁端發生單位轉角時的遠端剪力，或梁端發生單位移動時的遠端彎矩；

其它符合意義同前。

圖5 彈性地基梁形常數計算簡圖Fig.5 Calculation diagram of shape constants of elastic foun?dation beam

3 壩下箱涵結點平衡方程組

壩下箱涵地基梁桿件在內水壓力荷載p作用下，將產生固端彎矩和固端剪力，出現桿端位移（圖6），于是據箱涵地基梁桿件載常數與形常數，采用疊加原理，可得箱涵桿件桿端內力計算式：

圖6 彈性地基梁桿端內力與桿端位移簡圖Fig.6 Internal force and displacement at the end of the elastic foundation beam

式（23）也稱為箱涵桿件轉角位移方程。

式中：MAB、MBA、QAB、QBA表示箱涵桿件桿端內力；θA、θB、yA、yB表示箱涵桿件桿端位移；、、、表示箱涵桿件固端彎矩和固端剪力，即箱涵地基梁桿件載常數。

在得出箱涵桿件A B、A C；BA、BD；CA、CD；D C、D B的轉角位移方程后，則可分別建立箱涵結點A、B、C、D的力矩平衡方程

將箱涵桿件桿端內力計算成果代入式（24）～（27），聯立求解便可得到箱涵結點轉角與位移。

4 工程實例

某水庫壩下箱涵采用豎井取水，箱涵坐落于土基上，為C20鋼筋混凝土結構，混凝土彈性模量Ec=2.55×107kPa，土基彈性抗力系數k=10×103kN/m2。箱涵底板、頂板、側墻厚均為d=0.3m，計算寬度l=1.5m，計算高度h=1.9m，凈空尺寸1.2 m×1.6 m（寬×高）。底板承受內水壓力p1=216 kN/m2，頂板承受內水壓力p2=200 kN/m2。求箱涵在非均勻內水壓力作用下的彎矩與剪力。

解：取單寬箱涵b=1.0 m進行計算與分析。

工程實際問題表明，箱涵結構與荷載軸對稱，箱涵結點基本未知量只有θA與θC。下面計算箱涵特征參數。

圖7 壩下箱涵橫剖面尺寸圖Fig.7 Profile of the box culvert beneath dam

4.1 箱涵特征參數

（1）箱涵底板、頂板、側墻的截面慣性矩I

（2）箱涵底板、頂板、側墻的特征參數β

于是

（3）箱涵底板、頂板、側墻的形常數

箱涵底板受均布荷載作用，桿端對稱轉動，其形常數可將有關參數代入式（22）求算，即

類似箱涵頂板的形常數為

箱涵側墻頂端、底端形常數分別為

（4）箱涵底板、頂板、側墻的載常數

箱涵底板的載常數可將有關參數值代入式（6）、式（7）求算，即

類似箱涵頂板的載常數可將有關參數值代入式（8）、式（9）求算，即有

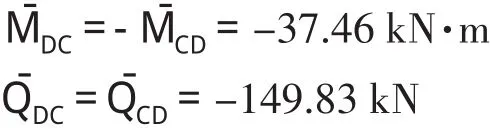
箱涵左側墻頂端的載常數可將有關參數代入式（13）、式（14）求算，即有

箱涵左側墻底端的載常數可將有關參數值代入式（15）、式（16）求算，即有

4.2 箱涵轉角位移方程

鑒于箱涵結構力荷載關于豎向呈軸對稱，于是箱涵剛結點轉角存在關系θB=-θA，θc=-θD，且結點線位移為零。據式（23），可得箱涵結點A、C的變矩：

4.3 箱涵結點平衡方程

據式（24）及式（26），可列出箱涵結點A、C的力矩平衡方程

將箱涵轉角位移方程中的MAB、MAC、MCA、MCD表達式代入式（a）、式（b）得

聯立求解式（c）、式（d）得θA=-1.6455×10-4；θC=1.7248×10-4

4.4 箱涵桿端內力

將求得的θA、θC值代入箱涵底板、頂板、側墻轉角位移方程式（23）中第1式、第2式，得如下桿端彎矩

此外，據轉角位移方程式（23）中第3式、第4式可求算出箱涵底板、頂板、側墻桿端剪力

4.5 求底板、頂板的跨中彎矩與側墻最大彎矩

據式（21），且注意到箱涵底板有y0==0，M0=MAB，Q0=-QAB，于是得

箱涵底板跨中處有：β1x=β1l=×0.4569×1.5=0.3427，查表得：φ1=0.9977，φ2=0.3425，φ3=0.0587，φ4=0.0068。并將以上計算值θAB、MAB、QAB及P1代入式（e），即得底板跨中彎矩為：

類似可得箱涵頂板彎矩計算式

將有關計算值與查表值代入得

箱涵左側墻受梯形荷載作用，類似于式（e），其彎矩計算式為

將有關參數值與計算值代入，得

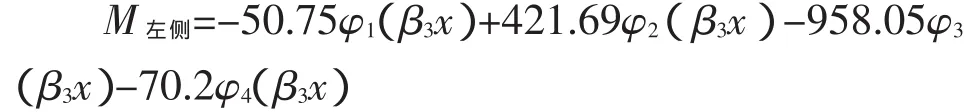
綜合以上計算結果，可得如圖8彎矩圖。

圖8 壩下箱涵內水壓力作用下彎矩圖（單位：kN·m）Fig.8 Bending moment of the box culvert beneath dam under internal water pressure

5 結語

采用地下框架結構模型，按左手直角坐標系，采用初參數法分析彈性地基梁與位移法建立箱涵桿件轉角位移方程，推導壩下箱涵受非均勻內水壓力作用下的內力與變位計算式。工程實例計算成果表明，箱涵底板、頂板與側墻相交直角處與桿件跨中部位通常為內力計算控制斷面，彎矩取極值，特別是側墻跨中部位外側有可能與土壓力荷載作用下的同向彎矩相疊加而加大結構內力。因此，為增強箱涵結點強度與剛度，消除或減小轉角處的應力集中，采取設置貼角、配設構造鋼筋及加強側墻跨中部位配筋等工程結構措施是必要的。此外，尚需指出，計及地基彈性抗力，可降低箱涵桿件最大彎矩值，且所獲成果可毫無困難地直接應用于水工矩形壓力隧洞洞段、矩形豎井與矩形調壓室襯砌結構計算。■

[1]熊啟鈞.涵洞[M].北京：中國水利水電出版社.2006.

[2]潘家錚.水工結構分析文集[M].北京：電力工業出版社.1981.

[3]龍馭球.彈性地基梁的計算[M].北京：高等教育出版社.1981.

[4]龍馭球，包世華.結構力學教程[M].北京：高等教育出版社.1988.

[5]蔡勇斌，周雪芳，蔡勇平，等.壩下涵管縱向內力計算與伸縮縫間距設計[J].大壩與安全，2012，（1）.

[6]蔡勇斌，劉女英，蔡勇平，等.圓形壩下涵管結構內力與變位計算及抗裂驗算解析法[J].大壩與安全，2010，（6）.

[7]張志堅，項和祖.石門水庫輸水管的加固設計[J].大壩與安全，2005，（1）.