圓柱體關于與對稱中心軸垂直且過對稱中心轉軸轉動慣量的簡單推導方法
羅時榮 左浩毅
(四川大學物理系,四川 成都 610064)
1 引言
轉動慣量是物體在繞定軸轉動時慣性大小的度量,質量連續分布的物體關于轉軸的轉動慣量表示為[1~3]

式中,r 是質量元dm 到轉軸的距離.利用式(1),選取適當的質量元,可得到一些質量對稱分布物體關于某些轉軸轉動慣量的解析表達式.質量元的選取是式(1)利用的關鍵,某些物體關于一些對稱軸容易選取適當的質量元,但有些物體關于某些對稱軸質量元的選取較為困難,比如質量均勻分布的圓柱體關于與其對稱中心軸垂直且過稱中心的轉軸,此時質量元的選取就不是那么容易,在文獻[4]中介紹了4 種不同質量元選取方法,基于這4 種方法雖然得到了該物體關于該轉軸的轉動慣量,但推導過程較為復雜,要用到兩重積分知識,而對于學習力學的大一學生積分知識才剛接觸,多重積分還很生疏,他們對這4 種方法的理解有一定困難.本文巧妙地將質量均勻分布圓盤選為質量元,利用轉動慣量的薄板垂直軸定理和轉動慣量平行軸定理,經過簡單的推導得到了質量均勻分布的圓柱體關于與其對稱中心軸垂直且過對稱中心轉軸的轉動慣量.
2 理論推導
2.1 質量均勻分布的薄圓盤關于一直徑轉軸的轉動慣量
為了求出質量均勻分布的實心圓柱體關于過其對稱中心且與對稱中心軸垂直的轉軸的轉動慣量,我們先求出質量均勻分布的薄圓盤關于其直徑轉軸的轉動慣量.
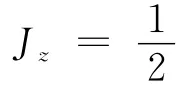

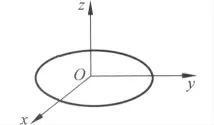
圖1 薄圓盤極其轉軸示意圖
由對稱性分析知薄圓盤關于任意直徑轉軸的轉動慣量都相等,據此可知Jx=Jy.將此等式和Jz表達式代入式(2)得
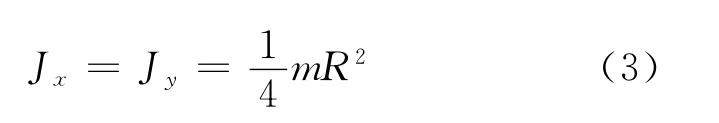
式(3)表示的轉動慣量就是薄圓盤關于任意直徑轉軸的轉動慣量.
2.2 質量均勻分布的實心圓柱體關于過其對稱中心且與對稱中心軸垂直的轉軸的轉動慣量
假定質量均勻分布的實心圓柱質量為m,半徑為R,長度為L,其對稱中心軸為z 軸,x 軸和y軸相互垂直,且過圓柱體對稱中心,并與z 軸垂直(如圖2所示).關于圖2中x 軸或y 軸的轉動慣量就是圓柱體關于過其對稱中心且與對稱中心軸垂直的轉軸的轉動慣量,由對稱性分析知,圓柱體關于過其對稱中心的任意直徑軸的轉動慣量都相等,所以下面只需求出關于x 軸的轉動慣量.為了求出關于x 軸的轉動慣量,我們先考查位于z處,厚度為dz的薄圓盤質量元(如圖2 所示)關于x軸的轉動慣量.如用ρ表示圓柱體的質量體密度,則質量元dm 的質量表示為


圖2 圓柱體極其轉軸示意圖
從質量元與z 軸的交點O1出發作一平行于x 軸的坐標 軸O1x1軸(如 圖2 所 示),O1x1軸 就 是 薄圓盤質量元的一直徑軸,利用式(3),可寫出該質量元對O1x1軸的轉動慣量,表示為
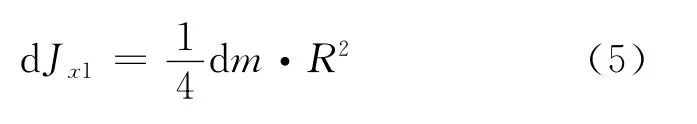
利用轉動慣量的平行軸定理可將質量元關于x 軸的轉動慣量表示為[1~3]
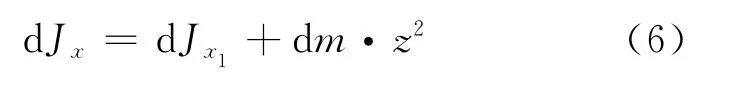
將式(4)、式(5)代入式(6)并對等式兩邊分別積分得圓柱體關于x 軸的轉動慣量,表示為

考慮到圓柱體的質量可表示為m=ρπR2L,式(7)可化簡為
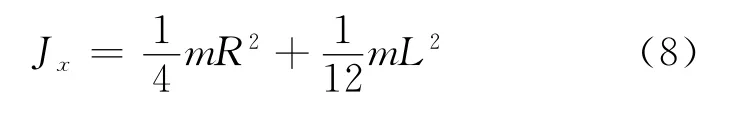
式(8)就是質量均勻分布的實心圓柱體關于過其對稱中心且與對稱中心軸垂直的轉軸的轉動慣量的一般表達式.
3 結論
本文將薄圓盤選為質量元,從薄圓盤通過盤心且與盤面垂直轉軸的轉動慣量表達式出發,利用轉動慣量薄板垂直軸定理和轉動慣量的平行軸定理,推導得到了實心圓柱體關于過其對稱中心且與對稱中心軸垂直的轉軸的轉動慣量的表達式,與文獻已有的推導過程相比,該文的推導方法簡單,便于學生理解和掌握.
[1]張三慧.大學基礎物理學(上冊)[M].北京:清華大學出版社,2003.146~149
[2]馬文蔚.物理學(上冊)[M].北京:高等教育出版社,2006.110~111
[3]王磊.大學物理學(上冊)[M].北京:高等教育出版社,2009.93~98
[4]史博,張輝,麻曉敏.圓柱體對垂直其中軸并過其中心的轉軸轉動慣量的幾種計算方法[J].物理與工程,2010,20(5):67~68

