對幾種不常見剛體轉動慣量的研究
周瑞雪
(貴州師范大學物電院,貴州 貴陽 550001)
引言
對于我們常見到的剛體,如均勻細棒、圓盤、圓環、圓柱等,教科書中已給出其轉動慣量的結論,我們也可以根據轉動慣量的定義計算出來,但對于另外一些剛體,如橢圓盤、球體、長方體、六面體等這些剛體,其轉動慣量的推導和計算教科書并沒有給出,有些剛體轉動慣量的計算上也有一定的難度,本篇文章將對這些剛體的轉動慣量在理論上進行一些研究,計算出它們的轉動慣量.
1 球體的轉動慣量
質量為m,半徑為R 的均勻球體,計算通過中心軸的轉動慣量.
方法:分割積分法[1]
如圖1把球分成很多的薄圓盤,薄圓盤的半徑為
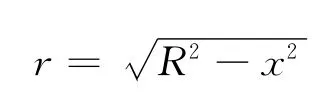
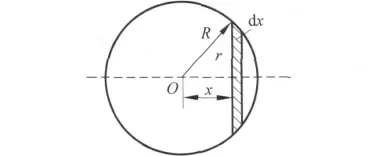
圖1
質量為
dm =ρdV =ρπr2dx
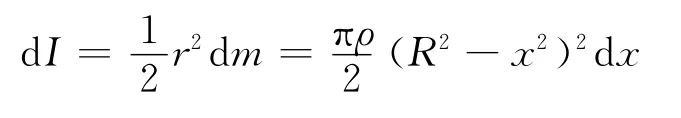
整個球的轉動慣量為
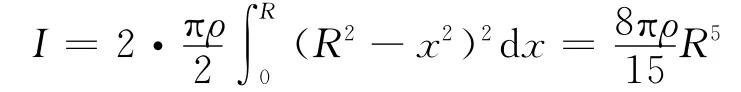
球的質量
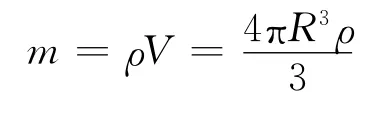
得到結果
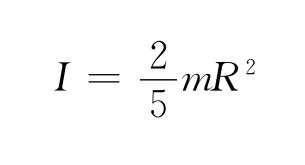
2 橢圓盤的轉動慣量
質量為m 的均質薄橢圓盤,其長半軸為a,短半軸為b,計算其對x、y、z軸的轉動慣量.
方法:質量投影法[2]
(1)首先計算對x 軸的轉動慣量
如圖2所示,將橢圓盤向y 軸投影得到長為2b的線段,質量仍為m,但質量非均勻分布,其質量線密度為
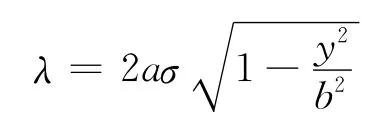
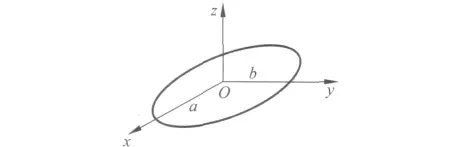
圖2
那么,長為2b的線段對x 軸的轉動慣量即系均質橢圓盤對x 軸的轉動慣量.
計算為
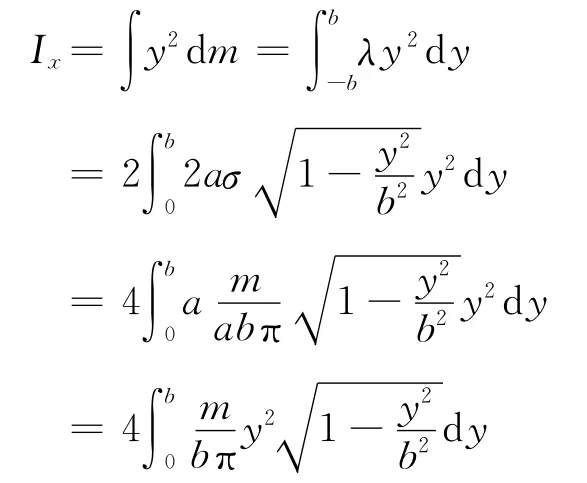
(2)數學計算[7]
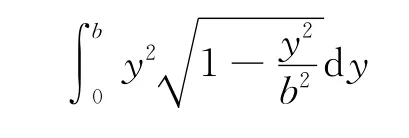
令
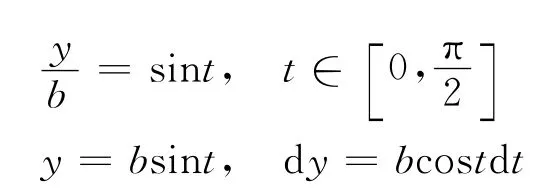
于是有
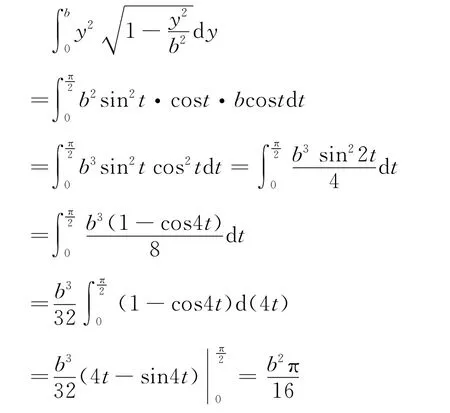
(3)結論
②同理得均質橢圓盤對y 軸的轉動慣量為
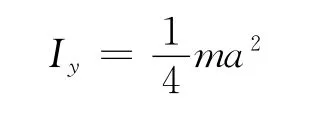
③利用正交軸定理得出對z軸的轉動慣量為
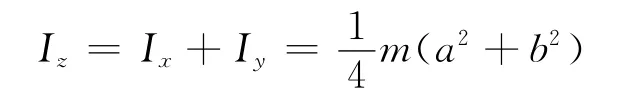
3 均質六面體的轉動慣量
如圖3所示,已知六面體的長為a、寬為b、高為c,其質量m 均勻分布,分別計算六面體對過質心 的x 軸、y 軸、z軸 的 轉 動 慣 量.
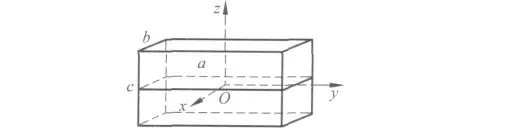
圖3
方法:質量投影法[3]
(1)首先計算對z軸的轉動慣量
將六面體向Oxy 平面投影得到長為a 寬為b的與z 軸垂直的矩形平面s,其質量仍為m 且均勻分布,這樣就把六面體對z 軸的轉動慣量轉化為均質矩形平面s對z 軸的轉動慣量;再將平面s向y 軸投影,得到長為a 的線段(細桿),其質量仍為m 且均勻分布,線段a對x 軸的轉動慣量為
即為平面s對x 軸的轉動慣量.
(2)同理得平面s對y 軸的轉動慣量為
(3)因此平面s對z 軸的轉動慣量為
此即均質六面體對z軸的轉動慣量.
(4)同理得均質六面體對x 軸、y 軸的轉動慣量
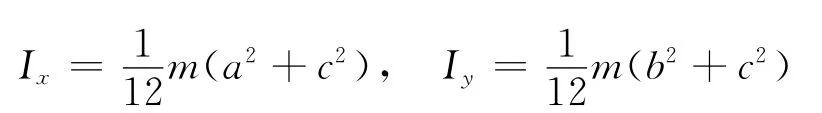
(5)討論 當a=b=c=l時,
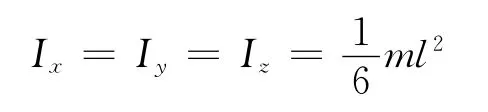
此即均質六面體轉化為均質正六面體.
4 均勻長方形薄板的轉動慣量
已知長方形薄板的長為a、寬為b、質量為m,轉動軸為其對角線,計算其轉動慣量.
方法:定積分法[5]
如圖4所示,取對角線為x 軸,原點為O 和它垂直的直線為y 軸,令σ為薄板的面密度.
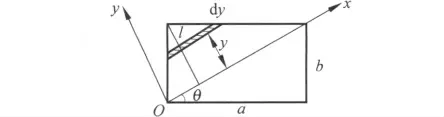
圖4
取一長方形窄條,長為l,寬為dy,由轉動慣量的定義得到繞對角線(x 軸)轉動的轉動慣量為
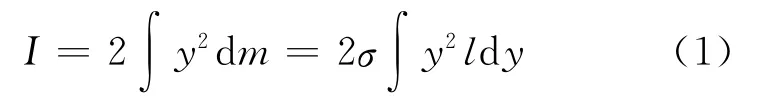
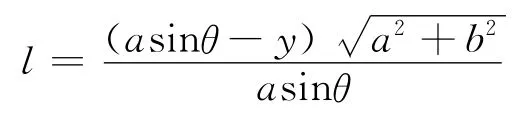
將l代入式(1)得
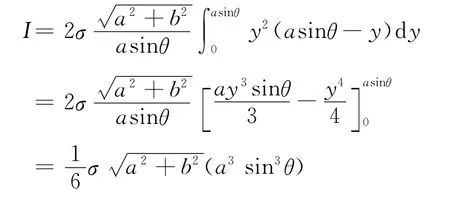
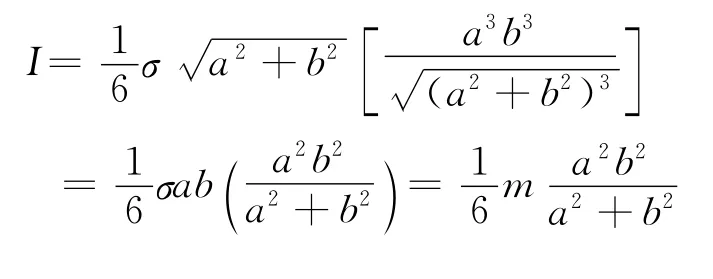
5 空心立方體柱的轉動慣量
如圖5所示,已知空心立方體(即由四塊正方形薄板構成),質量為m,邊長為2R,轉軸通過重心并和圖面垂直,計算其轉動慣量.
方法:為了求四薄板空心立方體繞過它的重心并垂直圖面的軸的轉動慣量,先求一塊板繞該軸的轉動慣量.
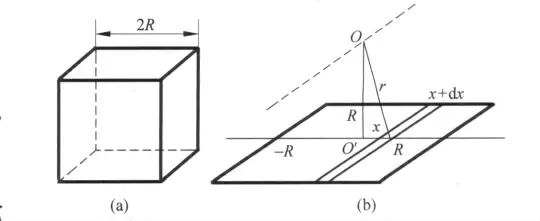
圖5
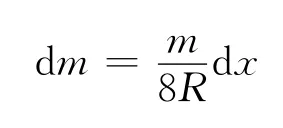
距O 軸的距離是
r2=R2+x2
所以,此窄條繞O 軸的轉動慣量是
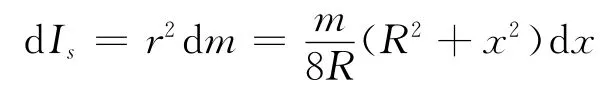
因此整個薄板繞O 軸的轉動慣量是
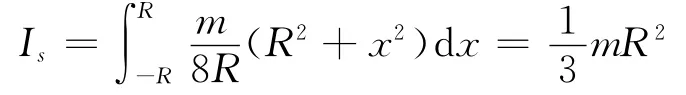
結論:由于四塊薄板對O 軸是對稱的,所以整個立方體對O 軸的總的轉動慣量為
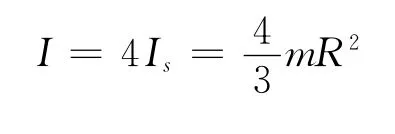
6 結束語
本文從轉動慣量的定義出發,采用了分割積分法,質量投影法等方法,計算了橢圓盤、六面體、正立方體,空心立方體、轉軸在對角線上的長方形薄板等幾種不常見剛體的轉動慣量,給出了教材中沒有的計算方法,對同行和研究這方面的學生有一定的借鑒作用.
[1][美]F.W.Sears.大學物理學(第一冊)[M].郭泰運譯.人民教育出版社,1979.274~278
[2]王永超.剛體轉動慣量的質量投影法[J].大學物理,2010,9
[3]漆安慎,杜嬋英.普通物理學教程:力學[M].北京:高等教育出版社,2005.222~226
[4]徐德,劉聚成,袁貞豐.大學物理學習題解答[M].北京:人民教育出版社,1989.319~324
[5]周衍柏.理論力學[M].北京:人民教育出版社,1982
[6]馬文蔚.物理學(上冊)[M]5版.北京:高等教育出版社,2008.104~111
[7]華東師范大學數學系.數學分析(上冊)[M]3版.北京:高等教育出版社,2001.224~225

