基于神經網絡的雙饋風電矢量控制系統轉速辨識

王娟平，程書華

（山西電力職業技術學院，山西 太原 030021）

變速恒頻風力發電系統，是一個復雜、不穩定、強耦合、多變量的非線性系統，其系統參數具有很強的不確定性，很難建立精確的數學模型。在很多研究中，人們將矢量控制應用于雙饋風力發電系統中，實現了發電機輸出頻率不再影響原動機轉速，發電機輸出電壓（或電流）的頻率、幅值、相位也不受轉子轉速和轉子瞬時位置的影響[1]，基本完成了風力發電這一非線性系統的解耦控制。

然而，傳統的矢量控制技術，大多采用位置傳感器來檢測轉子轉速，給風力發電系統帶來了較大的維護工作量，降低了風力發電機的可靠性和適應性。為此，近年來雙饋發電機的無速度傳感器矢量控制方法，成為研究風電系統的熱門課題。

文獻[2]提出一種基于轉子電流的模型，參考自適應系統（MRAS）的雙饋感應電機（DFIM）無速度傳感器控制方法；

文獻[3]通過采用PI自適應算法，構造了一種新型轉速辨識的無速度傳感器風電矢量控制方法；

本文在文獻[3]的基礎上，設計出一種基于神經網絡的雙饋風力發電機的轉速估計方法，并在MATLAB/Simulink環境下，對該系統進行動態仿真研究，研究結果表明，該轉速估計方法具有良好的快速逼近性。

1 無速度傳感器雙饋風電矢量控制系統原理

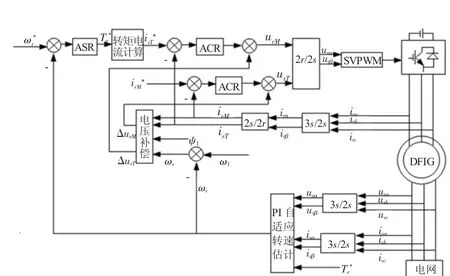
圖1 基于PI自適應轉速估計的無傳感器矢量控制系統框圖

圖1 為基于PI自適應法進行轉速估計的無傳感器風電矢量控制系統轉子側模型。從圖中可以看出，轉子側系統采用轉子電流、轉子轉速雙閉環控制。其中，內環為轉子電流控制環，通過檢測轉子相電流，經過3s/2s和2s/2r兩步變換，得到同步旋轉坐標系下的irM、irT兩個控制通道，通道中轉子電流的給定值與irM、irT比較后的誤差，經帶積分和輸出限幅的PI型電流調節器調節后輸出電壓控制量，該電壓控制量分別疊加前饋電壓補償量△urM、△urT后，得到轉子電壓控制量，轉子電壓控制量再經2r/2s變換、SVPWM調制后產生發電機轉子側實際所需的勵磁電壓和勵磁電流，實現雙饋風力發電矢量控制系統轉子側的解耦控制。

圖1矢量控制系統的外環為轉子轉速控制環，與電流內環類似，轉速的給定值與轉速的反饋值比較后所得的差值，經PI調節器調節后，得到發電機的輸出轉矩，輸出轉矩再經轉矩電流計算，得到轉子電流有功分量的給定值。而轉子電流無功分量的給定值，通常是按照電網對風力發電矢量控制系統的無功要求計算得到的。該系統中，電機轉速反饋值的檢測，是通過PI自適應速度辨識方法來估計的，利用自適應控制原理，使系統對轉子參數的魯棒性大大提高，但同時仍然引入了PI調節器，使得系統動態估計精度受到影響[3]。

2 神經網絡轉速辨識

神經網絡轉速辨識的基本原理，如圖2所示，采用離線訓練、在線運行的方法，對原系統的輸入、輸出數據直接學習，通過調節其權值來映射原非線性系統，實現以任意精度逼近該非線性系統，從而進行參數估計和轉速辨識。這種控制理論的自適應自組織能力、泛化能力和非線性映射能力很強，與傳統的PI調節自適應控制相比，可彌補其不足，使其對參數的變化和系統的噪聲具有很強的魯棒性[4]。

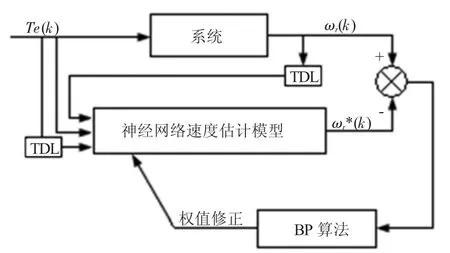
圖2 神經網絡轉速辨識的基本原理

圖2 中，“系統”是由PI自適應算法所建立的非線性模型，其非線性關系經過離散化后如下式所示：

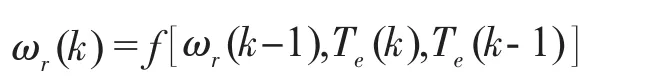
這一非線性關系，可以由神經網絡來映射[4]，只需提供足夠多的輸入、輸出樣本數據，對神經網絡進行嚴格的學習訓練，使該神經網絡逼近原PI自適應算法所建立的系統，進而映射原PI自適應算法所建立系統的非線性關系，實現用神經網絡模型對風力發電系統的控制。

在眾多的神經網絡模型中，基于BP算法的神經網絡（即BP網絡）發展最為成熟。在使用BP網絡時，關鍵問題在于神經網絡的結構設計上，即如何選擇網絡的層數和每層節點數。

本文使用的神經網絡轉速辨識模型，是對PI自適應算法的輸入、輸出樣本數據進行反復訓練改進后所確定的，其結構如圖3所示。

圖中，x1、x2和 x3為系統輸入，分別代表

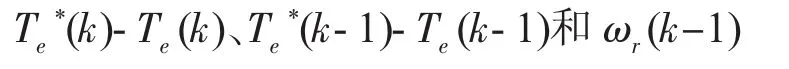
ωr為辨識對象的輸出，ωr*為神經網絡模型的輸出，選擇tan-sigmoid函數作為隱含層的激活函數，purelin函數作為輸出層的激活函數，可得網絡的訓練樣本集。

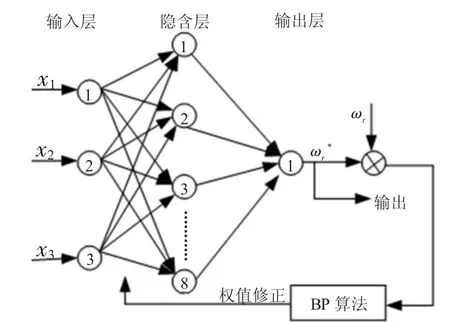
圖3 神經網絡轉速辨識結構模型

3 BP神經網絡控制系統仿真

以PI自適應速度估計為基礎，對基于PI自適應速度估計的無傳感器矢量控制系統中的PI調節器，用BP神經網絡來代替，對轉速進行辨識，得到了BP神經網絡速度辨識系統。圖4給出了MATLAB/Simulink環境下搭建的基于BP神經網絡的轉速辨識模型。

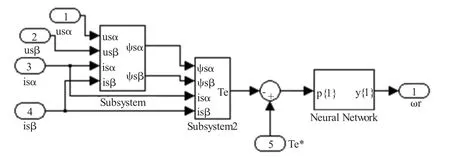
圖4 基于神經網絡的轉速辨識模型

圖5 為利用Matlab中的nntool工具箱建立的BP網絡，即神經網絡部分。

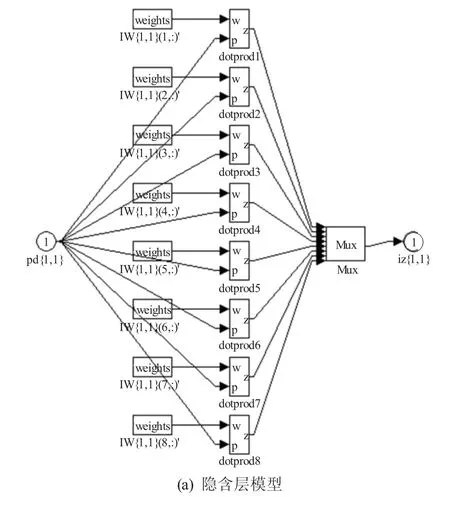
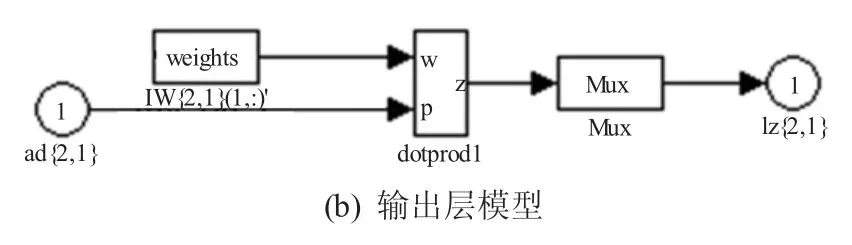
圖5 BP網絡模型

為驗證應用BP神經網絡估計發電機轉速的實際效果，對該系統作了仿真。

當發電機工作在亞同步速（ω=135 rad/s）和超同步速（ω=152 rad/s）時，其系統轉速的變化曲線分別如圖6和圖7所示。而當發電機的工作狀態從亞同步速（ω=135 rad/s）狀態切換到超同步速（ω=152 rad/s）狀態時，其系統轉速的變化曲線如圖8所示。圖中標有線標1的曲線為實際轉速曲線，標有線標2的曲線為PI自適應辨識轉速曲線，標有線標3的曲線為神經網絡辨識轉速曲線。

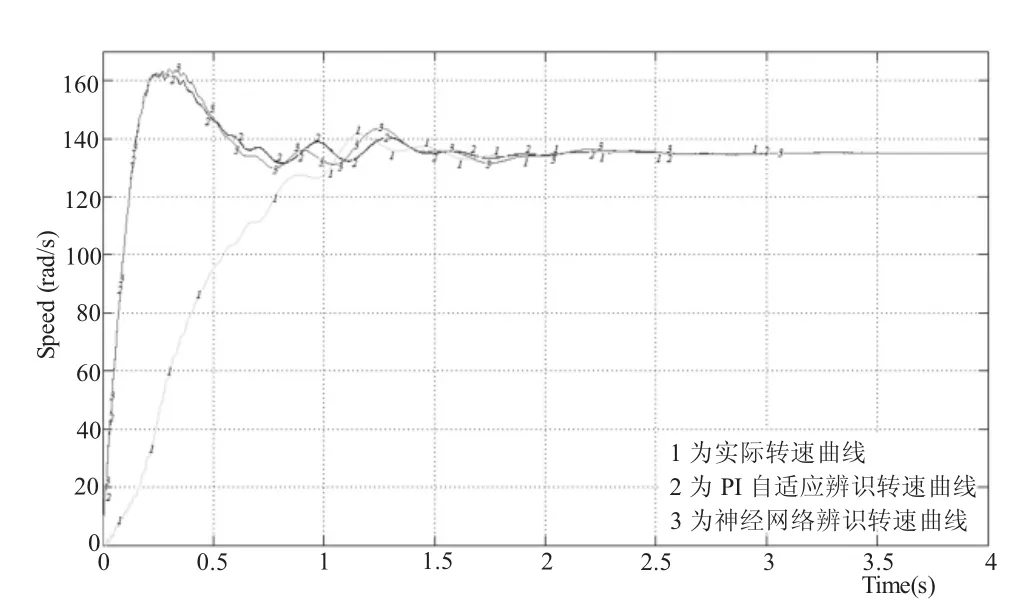
圖6 給定轉速ω=135 rad/s時發電機轉速變化波形

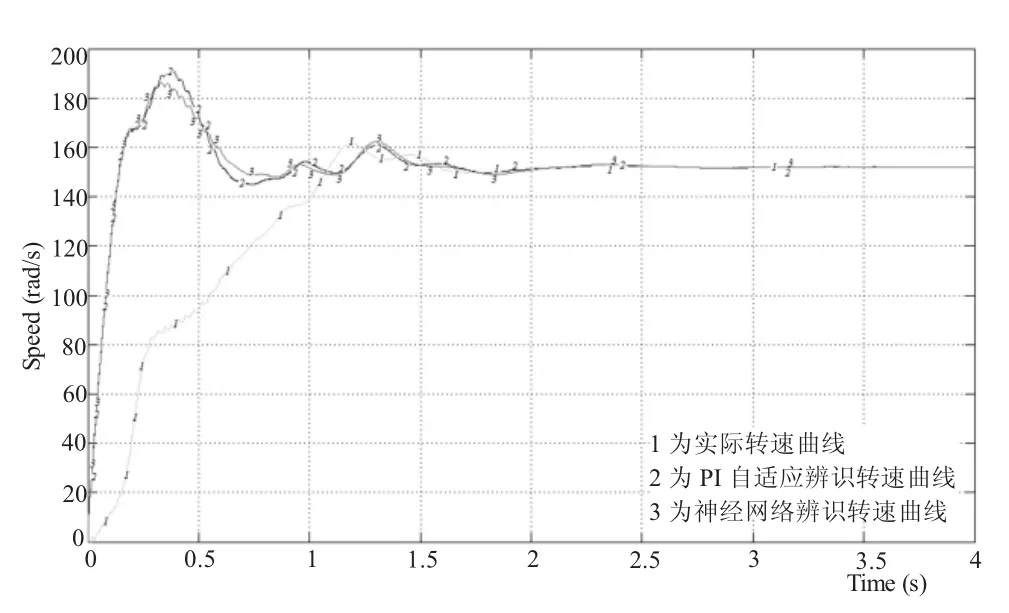
圖7 給定轉速ω=152 rad/s時發電機轉速變化波形

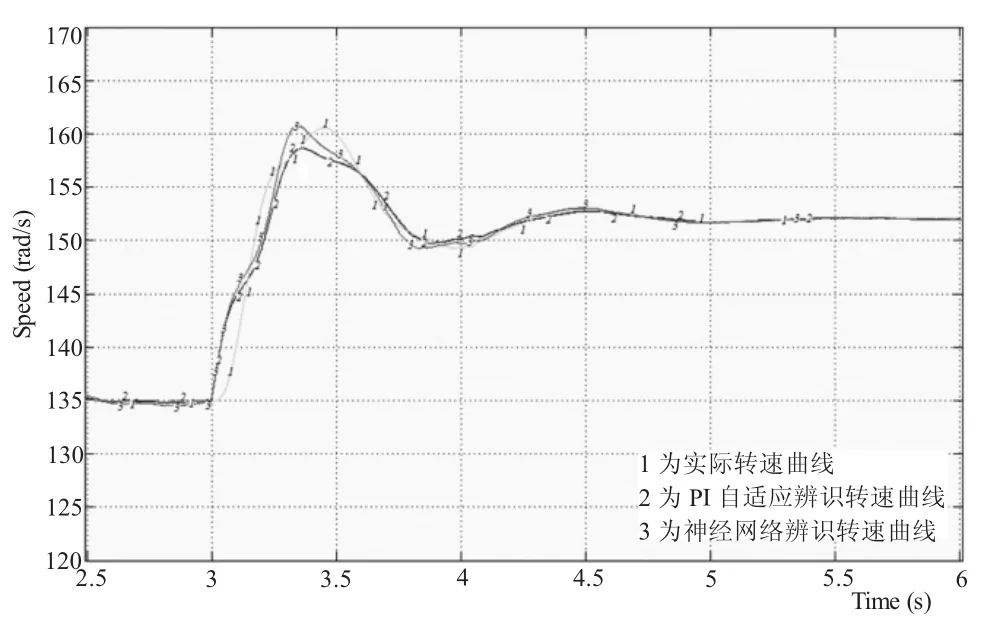
圖8 發電機從亞同步狀態切換到超同步狀態時的轉速變化波形

從圖6、圖7和圖8的轉速變化曲線可知，無論發電機工作于亞同步狀態、超同步狀態還是從亞同步狀態過渡到超同步狀態，采用PI自適應和神經網絡兩種方法對速度進行辨識的結果都優于實際轉速，表現在兩種方法的響應速度較快、抗外界干擾能力較靈敏、過渡過程中轉速的超調量較小。但三種轉速均能跟蹤轉速給定，且神經網絡對速度的辨識，很接近PI自適應法對速度的辨識。

4 結束語

神經網絡作為智能控制的一種，對于不能精確確定數學模型的非線性系統，具有良好的辨識能力和動態性能，采用該理論進行速度辨識，非常適用于雙饋風力發電矢量控制系統中發電機轉速的在線動態檢測。且該方法自學習、自適應能力很強，一旦經過嚴格訓練，便能以任意精度逼近原非線性系統，為非線性系統辨識提供了一個強有力的工具。

[1]劉寶英.并網型風力發電機組控制技術綜述[J].機電信息，2009，（36）：66-68.

[2]高 樂，周有慶，徐隆亞，等.基于轉子電流的雙饋感應電機無速度傳感器控制[J].電力系統自動化，2010，34(13)：61-65.

[3]李 嵐，王 穎.雙饋風力發電系統PI自適應速度估計[J].微特電機，2007，（3）：8-10.

[4]雷 華.感應電動機的神經網絡速度估計方法研究[D].重慶：重慶大學，2003.