Development of Linearizing Feedback Control with a Variable Structure Observer for Continuous Stirred Tank Reactors
Bachir Daaou*, Abdellah Mansouri, Mohamed Bouhamida and Mohammed Chenafa
1 Department of Sciences and Technology, Ibn-khaldoun University BP 78, Zaaroura Road, Tiaret, Algeria
2 Department of Electrical Engineering, E.N.S.E.T. Oran, Laboratory of Automatics and Systems Analysis (L.A.A.S)BP 1523 El’ M’naouer, Oran, Algeria
1 INTRODUCTION
Continuous stirred tank reactors (CSTR) are commonly used in the process industries. The process in the reactor is usually nonlinear with time-varying parameters. It is necessary to control these reactors to improve their behavior. In recent years, various design methods for nonlinear control strategies have been proposed. Most of them are based on differential geometric concepts [1-5]. This method allows a certain class of systems to be linearized using state feedback and coordinate transformations [6, 7]. Extensions of the method, such as adaptive linearization [8, 9], robust linearization [10], and asymptotically exact linearization [11], account for small model-plant-mismatch.
For the state estimation, many investigations deal with the observation techniques to estimate the state variables in chemical reactors [12-23].
The main purpose of this work is to develop an observer-based nonlinear control scheme for a CSTR.We apply the variable structure observer, as proposed by Walcott et al. [24] for estimating the concentration.The controller is constructed through feedback linearization. Since no separation principle exists for nonlinear systems, the study of the asymptotical stability of the closed-loop system including the observer dynamics is to be established, which is the main objective of this work.
In this work, the reactor model is presented. A variable structure observer for estimating concentration is constructed. For the closed loop control, we use Lyapunov argument to prove the closed loop stability.The closed-loop dynamic simulations are developed to illustrate the effectiveness of the proposed approach.
2 MATHEMATICAL MODEL OF REACTOR
The model for a first order irreversible exothermic reaction in a continuous stirred tank reactor (CSTR) is given by

The model can be non-dimensionalized by defining following dimensionless variables and parameters
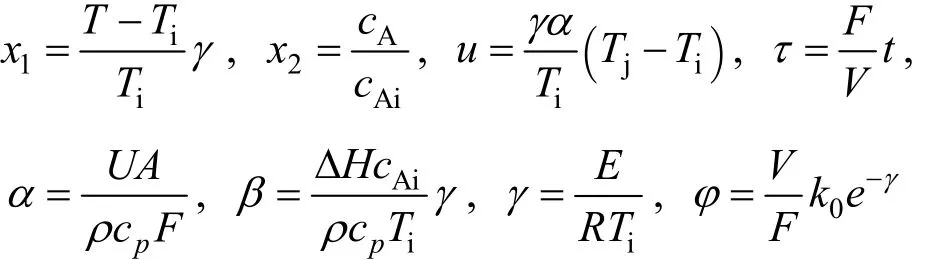
where x1is the dimensionless reactor temperature, x2is the dimensionless conversion and, u is the measured input.
The dimensionless equations for the CSTR can be written as
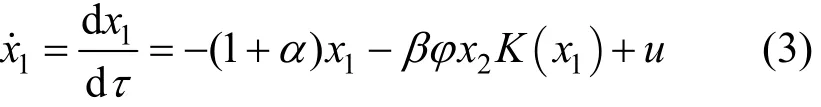

The reactor parameter values are given in Table 1.

Table 1 Parameter values of the reactor
3 OBSERVER DESIGN
The mathematical model of the chemical reactor has the following form
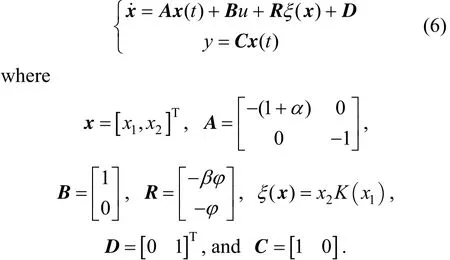
The main theoretical assumptions for the development of the observer strategy are listed below.
Assumption 1 The pair (A,C) is observable,i.e.,there exists a matrixGof appropriate dimensions such that the matrix0= -AAGCis stable and has a Lyapunov matrixPsatisfying
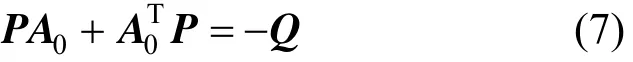
for positive definite design matrixQand the structural constraint

for nonsingular matrixF.
Assumption 2 The dynamics ()ξxis bounded,
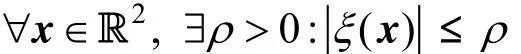
Theorem Under the above assumptions, the nonlinear observer given by
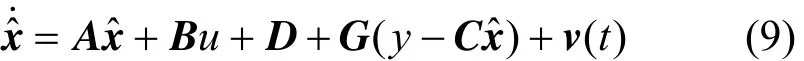
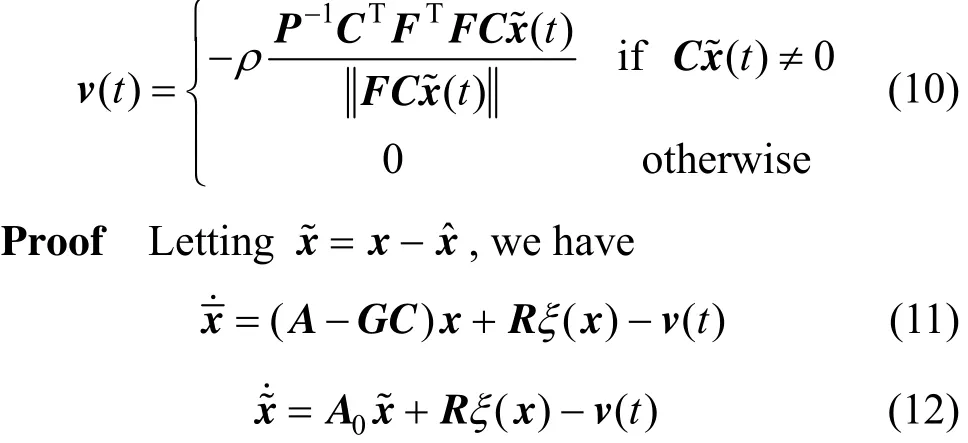
is an exponential observer for the system, Eq. (6),where Since (A0=A-GC) is Hurwitz, there exists a symmetric positive definite matrixPsatisfying Eq. (7).
DefineV(x? ) =x?TPx? as the Lyapunov candidate function. Then its time derivative is
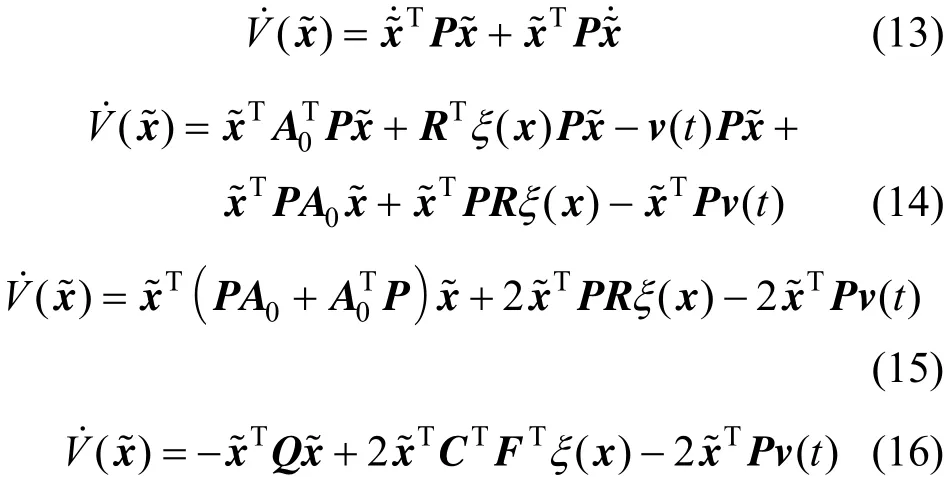
To continue the demonstration, there are two cases.Case 01 ()0t≠?
Cx
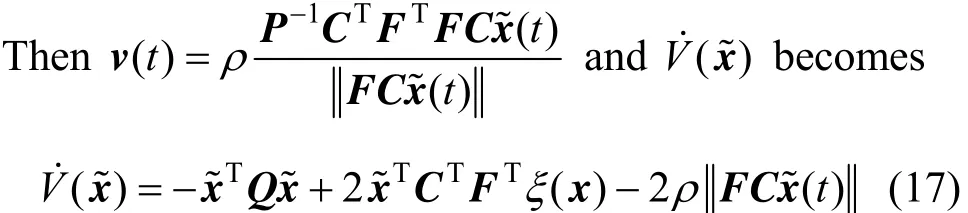
Using Assumption 2, we obtain
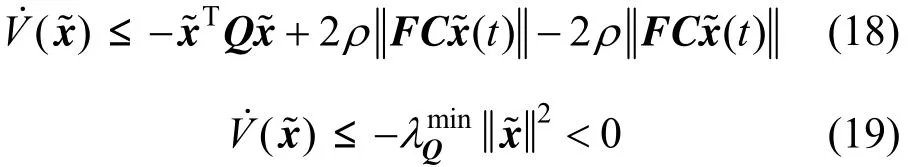
whereminλQis the minimum eigenvalue ofQ.
Case 02 () 0t=?Cx
In this case, Eq. (17) becomes

In both cases, the derivative of the Lyapunov function is negative, showing that the state estimation error converges asymptotically towards zero. This completes the proof of the Theorem.
4 CONTROL ALGORITHM
We design a control algorithm based on feedback linearization. The model of the chemical reactor, Eqs.(3)-(5), can be written as
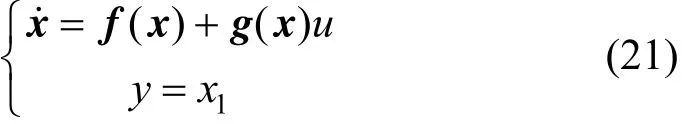
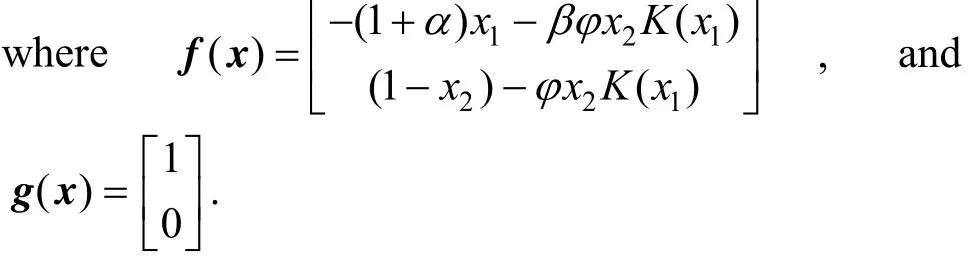
The relation between system input and the linearizing signal is

It should be noted that the state variables are estimated using an observer, then Eqs. (22) and (23) become

We choose ? such that the system is closed loop stable and achieves a desired setpoint at temperature.

Now consider the following assumption.
Assumption 3 Function ()ξx is globally Lipschitz with respect to x, i.e.
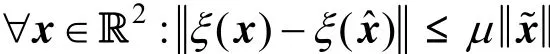
where μ denotes the Lipschitz constants of ()ξx.
Main result Consider the control law stated in Eq.(24) and the observer Eq. (9) with Eq. (10), if Assumptions 1-3 are satisfied and by selecting1δ and2δin the open left-hand side of the complex plane, the closed loop system described by Eq. (28) is globally asymptotically stable.
Proof Consider the following Lyapunov function candidate
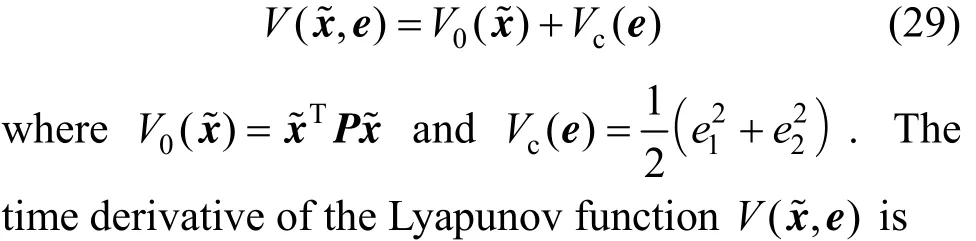
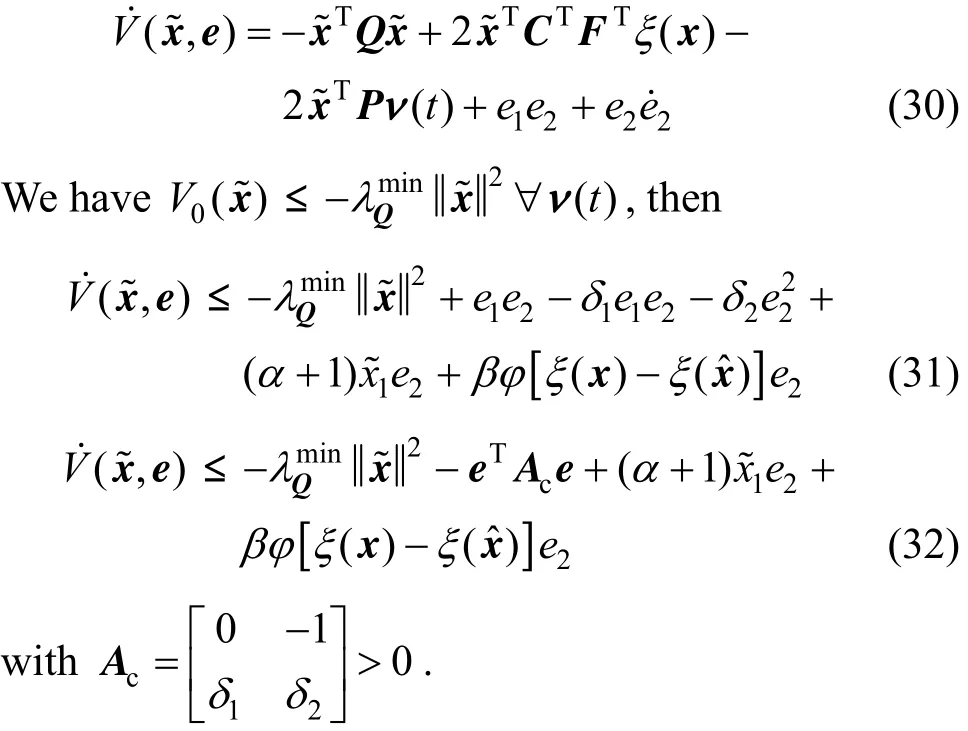
Using Assumption (3), inequality (32) becomes

Consequently, asymptotical stability of the closed-loop system is established.
5 SIMULATION RESULTS
Simulations, using MATLAB Software Package,are carried out to verify the effectiveness of the proposed method. The values of the model parameters used in simulation are given in Table1. To evaluate the observer performance, the system is simulated by assuming that the process is excited through a constant input signal u=1.5. This variable would be used later as the manipulated variable for control purposes.
The state initial conditions are set to (0)=xtion results obtained are depicted in Figs. 1 and 2. The speed of convergence can be modified by changing the values of the two matrixes G and Q. If Q is fixed and matrix G increases, higher speed of convergence is achieved but with undesirable chattering effect.

Figure 1 Actual and estimated dimensionless reactor temperaturereal value; estimated value
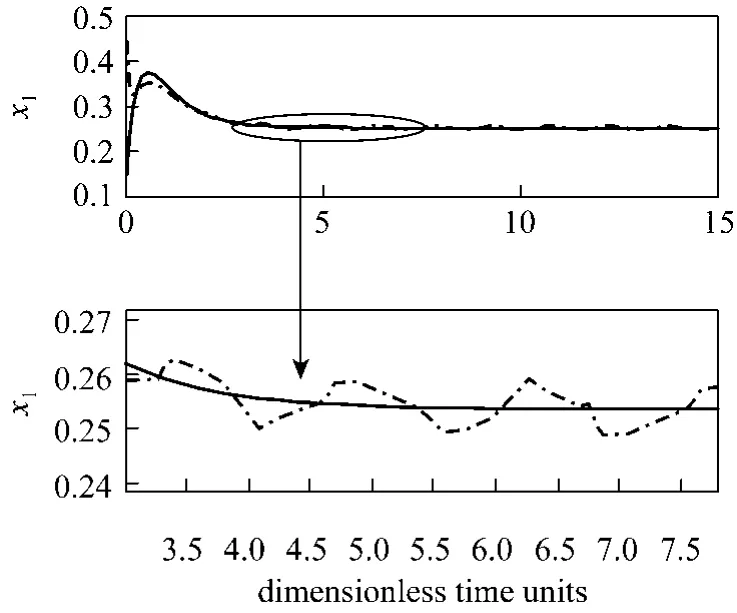
Figure 2 Actual and estimated dimensionless concentrationreal value; estimated value
Now, we study the performance of the observer by in a closed loop with the nonlinear control. The state initial conditions are set tox(0) = [1.8 0.65]Tandx? (0) = [2.3 0.8]T. Fig. 3 shows the measured temperature and the reference trajectory. The manipulated signaluis depicted in Fig. 4. It can be seen that the proposed observer/controller structure shows good performance in achieving the output regulation but the control action exhibits chattering, which may be unacceptable in practice. We use the boundary layer approach to eliminate chattering.
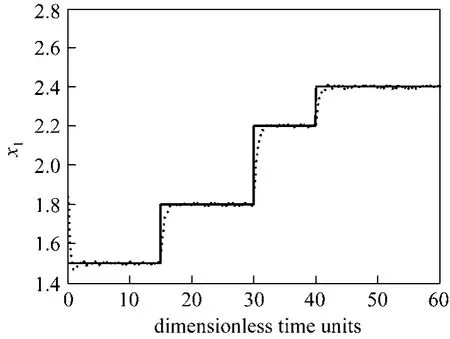
Figure 3 Closed-loop responsesetpoint; controlled output
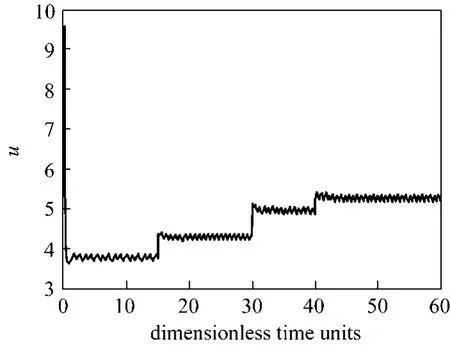
Figure 4 Control input
Finally, we examine the robustness of the proposed controllers in the presence of the measurement noise and model uncertainty.
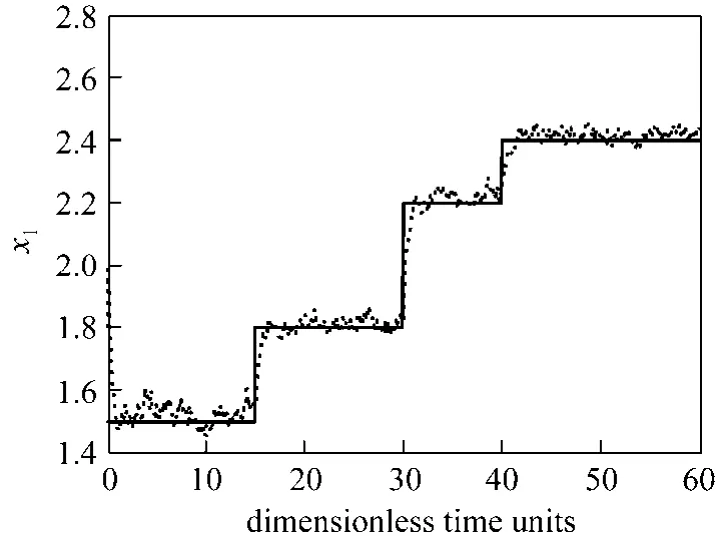
Figure 5 Closed- loop response in presence of measure noisessetpoint; controlled output
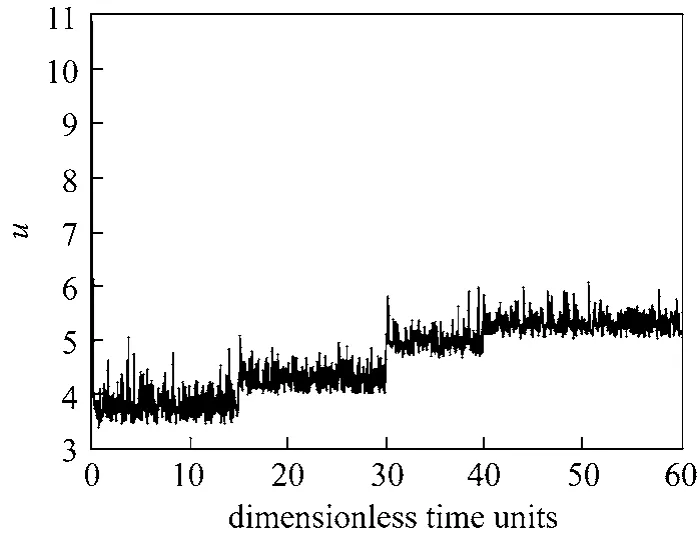
Figure 6 Control input in presence of measure noises
Case 01 Performance analysis in the presence of measurement noise In this case, white Gaussian noises with variances of ±5% are simultaneously added to the output measurement. The transient responses of temperature for the controller and their corresponding control actions are shown in Figs. 5 and 6 respectively.The set-point tracking behavior is very satisfactory.Note that the proposed controller maintains the temperature in a small neighborhood of the reference value despite the noise on the measurement.Case 02 Performance analysis in the presence of model uncertainty The major advantage of variable structure observers is that they can be made considerably more robust to parametric uncertainties. For this purpose, we consider a mismatch between the real activation energy and its value in the model. A difference up to 2% between the real parameter and its value in the model is considered. Simulation results are depicted in Figs. 7 and 8. The performance does not degrade significantly because the controller can well estimate the uncertainty.

Figure 7 Controlled dimensionless temperature for 2%increase in the activation energysetpoint; controlled output

Figure 8 Control input for 2% increase in the activation energy
6 CONCLUSIONS
In this paper, design of an observer-based control scheme using feedback linearization technique for temperature control of CSTR is addressed. The observer proposed in this study is basically the Luenberger observer with an additional switching term used to cope with system nonlinearities. The Lyapunov stability technique is used to establish the asymptotical stability of closed-loop system including the observer dynamics. The closed-loop performance of the controller is illustratedvianumerical simulations. It is shown that this controller is able to regulate the reactor temperature despite modeling uncertainties and noisy measurements.
1 Isidori, A., Nonlinear Control Systems, Springer-Verlag, New York(1989).
2 Jana, A.K., Samanta, A.N., Ganguly, S., “Globally linearized control on diabatic continuous stirred tank reactor: A case study”,ISA Trans.,44 (3), 423-444 (2005).
3 Khalil, H.K., Nonlinear Systems, 2nd edition, Prentice-Hall, Upper Saddle River, NJ (1996).
4 Kravaris, N., Chung, C., “Nonlinear state feedback synthesis by global input/output linearization”,AIChE J., 33 (4), 592-603 (1987).
5 Slotine, E., Li, W., Applied Nonlinear Control, Prentice-Hall, New Jersey (1991).
6 Gonzalez-Trejo, J., Ramirez, J.A., Fernandez, G., “Robust control with uncertainty estimation for feedback linearizable systems: Application to control of distillation columns”,J.Proc.Cont., 9 (3),221-231 (1999).
7 Henson, M., Seborg, D., “Input/output linearization of general nonlinear processes”,AIChE J., 36 (11), 1753-1757 (1990).
8 Sastry, S.S., Isidori, A., “Adaptive control of linearizable systems”,IEEE Trans.on Autom.Contr., AC34, 1123-1131 (1989).
9 Tyner, D., Soroush, M., Grady, C.G., “Adaptive temperature of multiproduct jackted reactors”,Ind.&Eng.Chem.Res., 38 (11), 4337-4344(1999).
10 Slotine, J.J.E., Hedrick, J.K., “Robust input-output feedback linearization”,Int.J.of Cont., 57 (5), 1133-1139 (1993).
11 Groebel, M., Allg?wer, F., Storz, M., Gilles, E.D., “Asymptotically exact I/O-linearization of an industrial distillation column”, In: Proceedings of the 1995 American Control Conference (ACC 95), Seattle, USA, 2648-2652 (1995).
12 Aguilar, R., Martínez-Guerra, R., Poznyak, A., “Reaction heat estimation in continuous chemical reactors using high gain observers”,Chem.Engi.J., 87 (3), 351-356 (2002).
13 Aguilar, R., Martinez-Guerra, R., Maya-Yescas, R., “State estimation for partially unknown nonlinear systems: A class of integral high gain observers”,IEE Proc.Contr.Theor.Appl., 150 (3), 240-244 (2003).
14 Aguilar, R., Martinez-Guerra, R., “State estimation for nonlinear systems under model unobservable uncertainties: Application to continuous reactor”,Chem.Eng.J., 108 (1-2), 139-144 (2005).
15 Aguilar, R., “Sliding-mode observer for uncertainty estimation in a class of chemical reactor: A differential-algebraic approach”,Chem.Prod. &Proc.Mod., 2 (3), 10 (2007).
16 Ahmed-Ali, T., Lamnabhi-Lagarrigue, F., “Sliding observer-controller design for uncertain triangular nonlinear system”,IEEE Trans.On Autom.Contr., 44 (6), 1244-1249 (1999).
17 Canudas de Wit, C., Slotine, J., “Sliding observers for robot manipulators”,Automatica, 27 (5), 859-864 (1991).
18 Daaou, B., Mansouri, A., Bouhamida, M., Chenafa, M., “A robust nonlinear observer for state variables estimation in multi-input multioutput chemical reactors”,Int.J.Chem.Reac.Eng., 6, A86 (2008).
19 Farza, M., Busawon, K., Hammouri, H., “Simple nonlinear observers for on-line estimation of kinetic rates in bioreactors”,Automatica, 34(1), 301-318 (1998).
20 Farza, M., Hammouri, H., Jallut, C., Lieto, J., “State observation of a nonlinear system: Application to (bio)chemical processes”,AIChE J.,45 (1), 93-106 (1999).
21 Gauthier, J.P., Bonard, G., “Observability for anyu(t) of a class of nonlinear system”,IEEE Trans.Autom.Contr., AC26, 922-926 (1981).
22 Gauthier, J.P., Hammouri, H., Othman, S.A., “A simple observer for nonlinear systems-application to bioreactors”,IEEE Trans.on Autom.Contr., AC37, 875-879 (1992).
23 Wang, G., Peng, S., Huang, H., “A sliding observer for nonlinear process control”,Chem.Eng.Sci., 52 (2), 787-805 (1997).
24 Walcott, B.L., Corless, M.J., Zak, S.H., “Comparative study of the nonlinear state-observation techniques”,Int.J.Contr., 45, 2109-2132(1987).
 Chinese Journal of Chemical Engineering2012年3期
Chinese Journal of Chemical Engineering2012年3期
- Chinese Journal of Chemical Engineering的其它文章
- Analysis of Absorption and Reaction Kinetics in the Oxidation of Organics in Effluents Using a Porous Electrode Ozonator*
- Flame Imaging in Meso-scale Porous Media Burner Using Electrical Capacitance Tomography*
- Modelling and Fixed Bed Column Adsorption of Cr(VI) onto Orthophosphoric Acid-activated Lignin
- Advances in Large-eddy Simulation of Two-phase Combustion (I)LES of Spray Combustion*
- Top-cited Articles in Chemical Engineering in Science Citation Index Expanded: A Bibliometric Analysis
- Adsorptive Removal of Para-chlorophenol Using Stratified Tapered Activated Carbon Column
