基于提升小波熵指標的梁板組合橋損傷識別研究

孫增壽，范科舉

（1.鄭州大學 土木工程學院，鄭州 450002；2.中鐵大橋局集團 第一工程有限公司，鄭州 450053）

鋼-混凝土組合結構可以充分發揮鋼材和混凝土這兩種材料的優點，具有自重輕、強度高、剛度大等優點，已被廣泛應用于橋梁工程當中。由多片型鋼梁與現澆鋼筋混凝土橋面板組成的梁板組合結構特別適用于中、小跨徑公路橋梁，如北京市從1985年建成第一座組合梁橋至今，共建成了60余座。在鋼筋混凝土梁板組合橋中，為了加快施工進度，縮減工期，也經常采用鋼梁和現澆混凝土板結構體系。

在梁板組合橋結構體系中，梁板之間采用剛性剪力連接件連接，一端植入梁中，另一端澆入鋼筋混凝土板中，使之形成一個整體而共同受力。所以，組合梁橋受力的關鍵所在就是連接部位的剪力連接件，它的作用主要有兩個方面：① 用來抵抗混凝土板與梁間的掀起作用，使得梁板共同受力；② 用來承受并傳遞梁與混凝土板之間的縱向剪力［1-2］。因此該處受力復雜，在橋梁多年服役后，由于振動、超載和環境等因素影響，有的橋梁剪力連接件損壞嚴重，已經影響到橋梁的正常使用。而剪力連接件通常埋植在結構內部，一般的檢測方法很難檢測其損傷位置。

小波變換在時、頻域都具有表征信號局部特征的能力，利用一個可以伸縮和平移的可變視窗，能夠聚焦到信號或函數的任意細節進行時、頻域處理，既可看到信號的全貌，又可分析信號的細節，適合分析和識別結構響應中其它方法難以發現的局部損傷信息，判別結構的損傷情況［3-4］。特別是 1995 年 Sweldens［5］提出的不依賴傅里葉變換的小波構造方法-提升格式，易于進行整數小波變換、非線性小波變換和小波逆變換，實現小波變換的原位計算，大大提高了運算速度，減小了運算量和存儲量［6-7］，這對在線檢測和識別結構損傷是十分有利的。

另外，在信息論中常用譜熵表示每個符號所提供的平均信息量和信源的平均不確定性。所分析信號的譜熵越大，信號的不確定性就越大。但在譜熵計算過程中，基于快速傅里葉變換的功率譜估計只能反映信號的平均功率分布，不包含信號的任何時域變化信息。而用小波變換代替快速傅里葉變換所得到的小波熵即可表征信號不確定性在時域的變化情況，也可表征信號的頻域特征［8］。

為此，本文將提升小波引入到熵譜分析中，提出了結構響應的提升小波時間熵和相對提升小波熵指標，采用基于提升小波熵的損傷識別方法，判別梁板組合橋中剪力連接件的損傷時刻和損傷位置。

1 提升小波變換基本理論

提升小波是一種構造緊支集雙正交小波的新方法，基本提升過程分為三步：剖分、預測和更新。在實現中，最常用惰性小波做數據集的剖分；預測的目的是消除剖分后留下的冗余，給出更緊湊的數據表示；更新是為了使某一全局性質得以保障。提升小波的構造方法是基于多相矩陣P（z）或?P（z）因式分解的提升格式。

（1）剖分

剖分（Split）是將原始信號s0［n］分為兩個互不相交的子集和，即even1［n］和odd1［n］，每個子集的長度是原子集的一半。通常是將一個數列分為偶數序列和奇數序列，即：

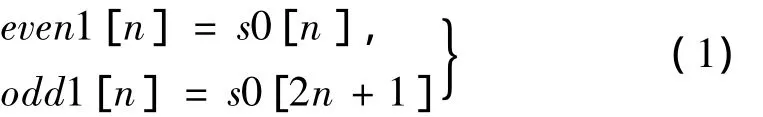
（2）預測

預測（Predict）是利用偶數序列和奇數序列之間的相關性，由其中一個序列（一般是偶序列even1［n］）來預測另一個序列（一般是奇序列odd1［n］）。實際值odd1［n］與預測值P（even1［n］）的差值d1［n］反映了兩者之間的逼近程度，稱之為細節系數或小波系數，對應于原信號的高頻部分。一般來說，數據的相關性越強，則小波系數的幅值就越小。如果預測是合理的，則差值數據集d1［n］所包含的信息比原始子集odd1［n］包含的信息要少得多。預測過程如下：

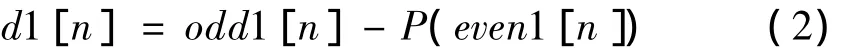
式中：P（·）表示預測算子。預測算子P可用預測函數Pk來表示，函數Pk可取為even1［n］中的對應數據本身或even1［n］中的對應數據的相鄰數據的平均值，或者其他更復雜的函數。

（3）更新

經過剖分步驟產生子集的某些整體特征（如均值）可能與原始數據并不一致，為了保持原始數據的這些整體特征，需要一個更新（Update）過程。將更新過程用算子U（·）來代替，其過程如下：

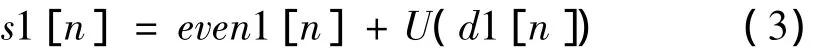
其中，s1［n］為s0［n］的低頻部分；與預測函數一樣，更新算子也可以取不同函數。P與U取不同的函數，可構造出不同的小波變換。

至此，提升方法實現了信號在一個尺度上的小波分解。細節信號d1［n］是1尺度上的小波系數，反映了原始信號中的高頻部分；逼近信號s1［n］為1尺度上的尺度系數，反映了原始信號中的低頻部分；因此可以構造具有某種特性的小波函數和尺度函數。提升格式在j尺度上的分解與重構如圖1所示。

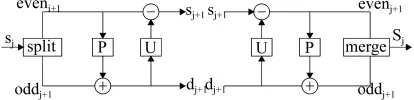
圖1 提升方法分解與重構示意圖Fig.1 The diagrammatic sketch of decomposition and restucting of lifting scheme

2 提升小波熵指標

2.1 相對提升小波能量

為了計算信號的提升小波熵值，這里先引入相對提升小波能量。對給定信號序列，通過提升小波變換可以得到不同尺度下的小波系數，定義每一尺度下的小波能量為該尺度下提升小波系數的平方和：

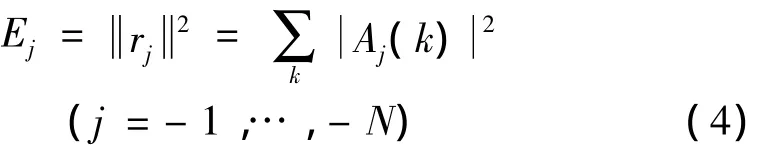
則信號序列的總能量為：

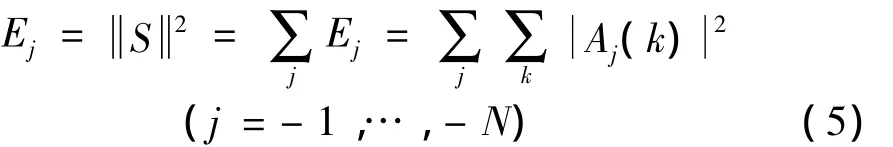
式中：Aj（k）為第j尺度下的提升小波系數。

相對提升小波能量可定義為：

由式（6）可見，相對提升小波能量Pj之和為1，同時也反映出Pj分布在時間軸上的密集程度，這就給出了一種檢測和識別信號有無異常特征的工具和方法。

2.2 提升小波時間熵

根據Shannon熵理論，提升小波熵定義如下［9］：

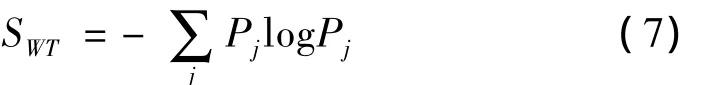
首先對給定信號序列s（t）進行提升小波變換，然后在變換系數序列上設定一滑動窗，設窗口寬度為τ∈N，滑動系數μ∈N，那么滑動窗為：

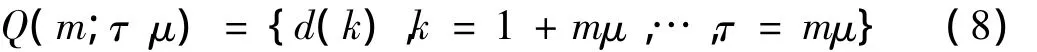
式中，m=1，2，…，M，其中M=（N- τ）/μ∈N，為窗口數量。依次在滑動窗內應用式（7）求提升小波熵，得到信號提升小波熵隨時間的變化規律，稱之為提升小波時間熵。在j尺度下的提升小波時間熵為：

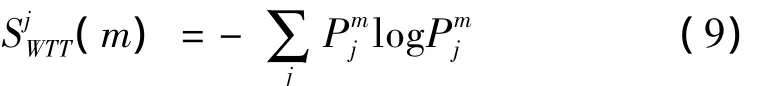
在每一尺度下計算信號的Sj WTT（m），并在時間軸上繪制提升小波熵的變化曲線，進而可根據明顯的提升小波時間熵峰值識別信號中的突變信息。

2.3 相對提升小波熵

給定兩組不同的信號，采用提升小波對信號進行分解變換，設它們的相對提升小波能量分布分別為Pj和Qj，定義相對提升小波熵為：

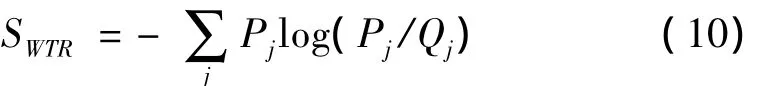
對于結構損傷檢測而言，可將兩組信號分別看作是結構損傷前后的動力響應信號，從式（10）不難看出，若結構沒有發生損傷，相對提升小波能量分布Pj和Qj基本上相同，這時相對提升小波熵值接近零；當結構存在損傷時，結構上各點動力響應的相對提升小波能量分布就會發生變化，這時相對提升小波熵就會偏離零點，特別是靠近損傷位置處的偏離較大。因此，可根據明顯的相對提升小波熵峰值來識別結構損傷位置。

3 基于提升小波熵的梁板組合橋損傷識別

結構損傷識別往往是結構兩種狀態下自身特性或響應之間的比較，它包括兩種情況：①結構損傷發生在連續監測過程中，在所測動力響應信號中隱含有損傷引發的突變信息；②擁有結構完好狀態下的動力特性和動力響應信號，可通過對比損傷前后這些參數的變化情況來判斷結構的損傷狀況。無論哪種情況，一旦結構發生或是存在損傷，損傷前后結構響應信號的提升小波熵都將發生明顯的幅值變化。下面通過梁板組合橋的數值模擬方法對兩個提升小波熵指標的敏感性和識別效果進行分析。

3.1 諧波函數分析

采用式（11）所示諧波函數，其時程曲線如圖2所示，在前10 s中包含1 Hz、2 Hz、和5 Hz三個頻率段，而在后10 s中1 Hz的頻率變為0.999 Hz，僅變化千分之一，相當于結構剛度發生微小變化。

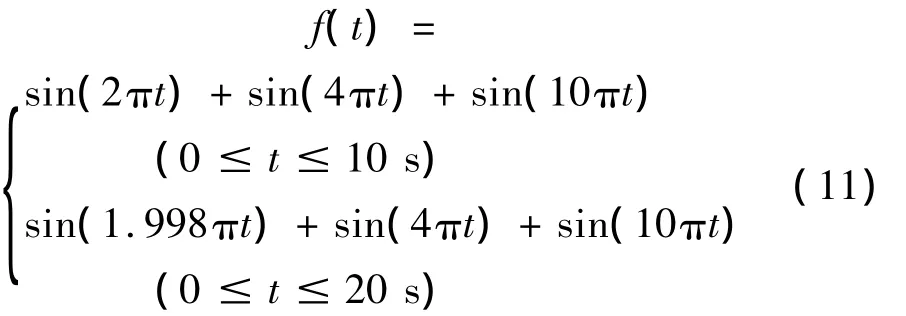
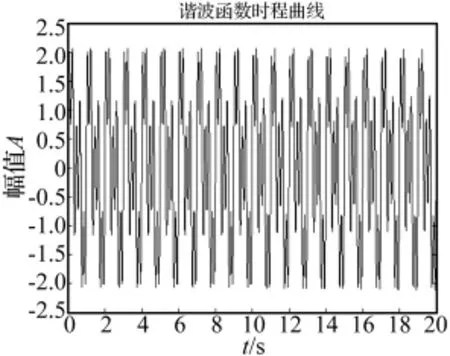
圖2 諧波函數時程曲線Fig.2 Time-history curve of harmnic function

下面通過提升小波熵指標來識別信號組分頻率的微小變化。首先對諧波函數進行提升小波變換，然后在提升小波變換的基礎上設定一滑動窗，依次按式（9）計算各窗口的提升小波時間熵，計算結果如圖3所示。從圖3可以看出，提升小波時間熵在10s處存在明顯的突變，成功識別出諧波函數在10s時刻信號組分頻率的微小變化。與文獻［9］和一般小波變換結果比較，提升小波時間熵的突變幅值較小波時間熵的突變幅值大，是后者的1.7倍，更容易識別損傷時刻和損傷位置，且計算速度快。

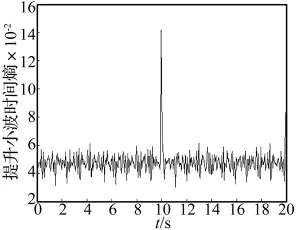
圖3 諧波函數提升小波時間熵Fig.3 Lifting wavelet time entropy of harmnic function

3.2 梁板組合橋的數值模擬

以圖4（a）所示梁板組合橋為例進行分析研究，為單跨三梁結構形式。鋼梁長6 m，翼緣板厚度為0.018 m、寬度為0.15 m，腹板厚度為0.008 m、高度為0.3 m。混凝土板厚度為0.05 m、寬度為1.14 m、長度為6 m。在每根鋼梁的上翼緣板上布置兩列9排栓釘剪力連接件，列間距75 mm，排間距600 mm，使鋼梁的上翼緣與混凝土板緊密連接，共同受力，剪力連接件的位置如圖4（b）所示。

采用有限元方法計算梁板組合橋在沖擊荷載下的加速度響應，在有限元建模過程中，混凝土板采用SOLID65單元，鋼梁采用SHELL63單元，剪力連接件采用線性彈簧單元，通過生死單元來控制剪力連接件的損傷。梁板組合橋的損傷工況如表1所示，模擬不同時刻、不同位置的剪力連接件損傷。

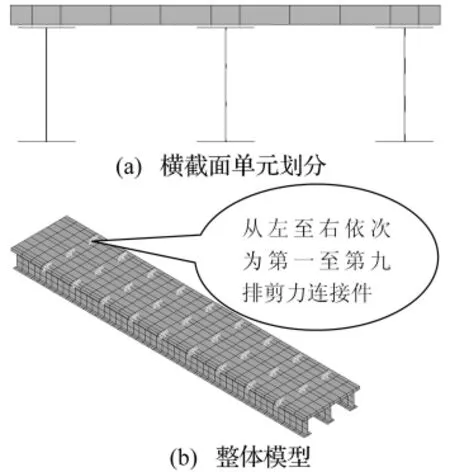
圖4 梁板組合橋有限元模型Fig.4 The finite model of beam-slab composite bridge

表1 梁板組合橋損傷工況表Tab.1 The damage scenarios of beam-slab bridge

在梁板組合橋有限元動力分析計算中，采用沖擊力進行激勵，沖擊力持時0.016 s，沖擊力時程如圖5所示，采樣頻率取1 000 Hz，采樣時間取1.000 s。圖6所示為提取的一節點的加速度響應時程曲線，曲線光滑漸變收縮，單從信號本身無法識別結構損傷情況。

圖5 沖擊力時程曲線Fig.5 Time-history curve of impact force

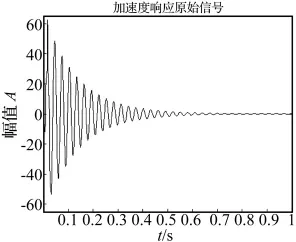
圖6 梁板組合橋節點加速度時程曲線Fig.6 The acceleration time-history curve of a node of beam-slab bridge

采用D4小波對提取的加速度動力響應信號進行提升小波變換，并在提升小波系數序列上加滑動窗函數，依次按式（9）計算各窗口的提升小波時間熵，結果如表2柱狀圖所示。對工況一，提升小波時間熵在0.4 s時刻存在明顯峰值，這正好與設定的0.4 s時刻剪力連接件發生損傷相一致，說明梁板組合橋在0.4 s的時刻部分剪力連接件失效。對工況二，提升小波時間熵在0.3 s和0.4 s時刻均存在明顯峰值，說明此刻的信號發生了異常，對應著結構在這一時刻發生了損傷；這也與設定的損傷時刻相一致，說明梁板組合橋在0.3 s和0.4 s的時刻部分剪力連接件失效。因此，對于發生在連續檢測過程當中出現的損傷，采用提升小波時間熵可以有效地識別，包括個別剪力連接件的破壞。同樣，也顯示出比小波時間熵突變幅值大的優勢。

為了進一步確定損傷剪力連接件的位置，依次提取橋面板中線上31個節點損傷前后的加速度響應，在相同尺度下對各節點損傷前后加速度響應信號進行提升小波變換，以損傷前梁板橋為基準，按式（10）求損傷梁板橋加速度響應信號的相對提升小波熵，分析結果如表2折線圖所示，顯示出各節點相對提升小波熵的分布情況。對工況一，在節點16位置出現明顯的相對提升小波熵峰值，說明損傷位置位于跨中，與工況一設定的剪力連接件損傷位置一致，準確識別出剪力連接件損傷位置。對工況二，在兩處損傷情況下，也準確識別出剪力連接件損傷位置。

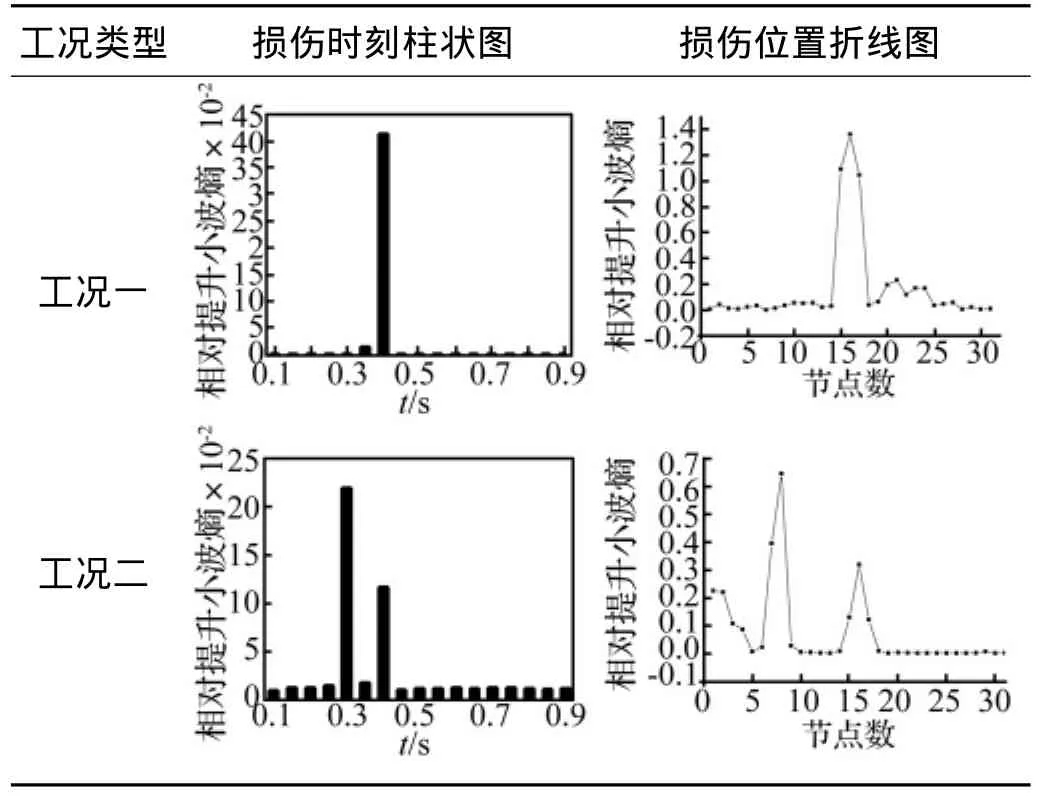
表2 梁板組合橋損傷時刻和損傷位置識別結果Tab.2 The identification result of damage time and location of beam－slab bridge

4 結論

本文將提升小波和信息熵有機結合起來，提出了提升小波時間熵和相對提升小波熵指標，并用于梁板組合橋剪力連接件損傷的檢測和識別，根據分析結果可得出以下結論：

（1）提升小波時間熵對結構響應中的突變信號比較敏感，可用于梁板組合橋健康監測系統中在線檢測和判定結構損傷；

（2）以完好梁板橋動力響應為基準，結構發生損傷后，各測點動力響應信號的相對提升小波熵將發生不同程度的變化，但損傷位置附近測點的相對提升小波熵譜值變化最為明顯，根據相對提升小波熵指標可以準確判定梁板組合橋剪力連接件的損傷位置。

［1］胡達和，謝志紅.鋼與混凝土組合梁橋在北京的應用［J］.市政技術，2003，21（2）：80-84.

［2］辛學忠，張曄芝.我國鐵路鋼-混凝土結合梁橋技術發展思考［J］.橋梁建設，2007，5：12-16.

［3］孫增壽.基于小波的土木工程結構損傷識別方法研究［D］.福州：福州大學，2006.

［4］ 張德豐.MATLAB小波分析［M］.北京：機械工業出版社，2009.

［5］ Daubechies I，Sweldens W.Factoring wavelet transforms into lifting steps［J］.Journal of Fourier Analysis and Application，1998，4（3）：245-267.

［6］孫增壽，范科舉，張 波.基于第二代小波變換的結構損傷檢測研究進展［J］.鄭州大學學報，2010，31（1）：1-5.

［7］ Rosso S A，Blanco S.Wavelet entropy：a new tool for analysis of short duration brain electrical signals［J］.Journal of Neuroscience Methods，2001，105：65-75.

［8］印欣運，何永勇，彭志科，等.小波熵及其在狀態趨勢分析中的應用［J］.振動工程學報，2004，17（2）：165-69.

［9］ Ren W X，Sun Z S.Structural damage identification by using wavelet entropy［J］.Engineering Structures，2008，（30）：2840-2849.