大尺度水下綜合試驗(yàn)?zāi)Ｐ屯弦愤\(yùn)動特性研究

，，

(1.中國船舶科學(xué)研究中心，江蘇 無錫 214082；2.清華大學(xué) 航天航空學(xué)院，北京 100084)

目前，開展水下航行體破損、大攻角、水下拖曳等非正常工況下或應(yīng)急工況下的運(yùn)動特性研究時[1-4]，小尺度模型的尺度效應(yīng)難以克服，出于安全考慮，實(shí)船試驗(yàn)也難以進(jìn)行。鑒于特殊工況下水下航行體的運(yùn)動特性的復(fù)雜性和影響因素多等原因，除依靠理論計算分析之外，大尺度模型試驗(yàn)也是重要的研究手段；此外，理論計算結(jié)果也需要經(jīng)過大尺度模型試驗(yàn)的驗(yàn)證與修正。因此，大尺度水下綜合試驗(yàn)?zāi)Ｐ统蔀樗潞叫畜w特殊工況下運(yùn)動特性研究的重要手段之一。

本文主要研究大尺度水下綜合試驗(yàn)?zāi)Ｐ屯弦愤\(yùn)動特性。大尺度水下綜合試驗(yàn)?zāi)Ｐ涂傞L25 m，最大設(shè)計航速4 m/s，具備自航能力。試驗(yàn)水域?yàn)橐宦短焖兀Ｐ偷淖畲笮谐?00 m，其中加速段長70 m，勻速試驗(yàn)段長80 m，減速段長50 m。受試驗(yàn)水域的限制，模型無法通過自身推進(jìn)器在較短的距離內(nèi)完成加減速過程，因此考慮采用如圖1所示的纜繩牽引方式完成模型的加減速運(yùn)動過程。

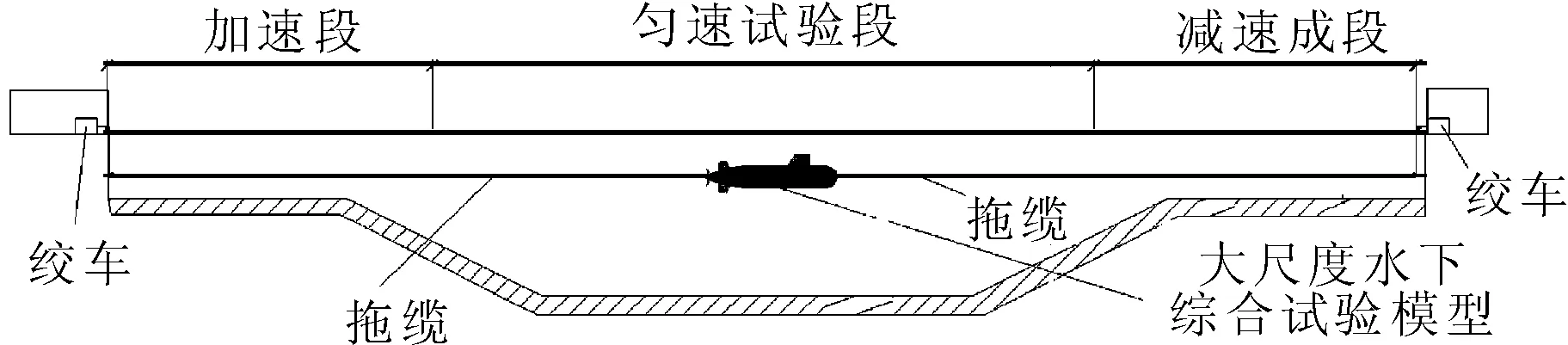
圖1 試驗(yàn)?zāi)Ｐ凸ぷ鞣绞绞疽?/p>

拖纜拖曳的試驗(yàn)?zāi)Ｐ褪艿酵饬_動時，可能會產(chǎn)生運(yùn)動的振蕩發(fā)散，影響試驗(yàn)。尤其是鉛垂面內(nèi)的擾動可能會造成模型較大的垂向位移和較大的縱傾，導(dǎo)致模型觸底。本文通過數(shù)值計算，總結(jié)規(guī)律，選擇合適的預(yù)緊力避免模型運(yùn)動發(fā)生振蕩發(fā)散；對操舵試驗(yàn)的兩種典型工況進(jìn)行計算分析，給出保證試驗(yàn)過程中的運(yùn)動穩(wěn)定性和安全性的操舵限制條件。

1 計算模型

試驗(yàn)?zāi)Ｐ团c拖纜組成了一個三維空間的連續(xù)彈性振動體系統(tǒng)。由于系統(tǒng)在鉛垂面內(nèi)的運(yùn)動和在水平面內(nèi)的運(yùn)動具有相似性，并且鉛垂面內(nèi)的運(yùn)動關(guān)系到試驗(yàn)?zāi)Ｐ偷陌踩虼朔治鱿到y(tǒng)鉛垂面內(nèi)的運(yùn)動意義重大。將系統(tǒng)簡化為鉛垂面內(nèi)的二維系統(tǒng)。根據(jù)經(jīng)驗(yàn)估算，試驗(yàn)?zāi)Ｐ屯侠|的直徑不大于25 mm，拖纜的總重量不大于1 t，而試驗(yàn)?zāi)Ｐ偷娜潘繛?10 t，顯然試驗(yàn)?zāi)Ｐ涂勺鳛橄到y(tǒng)中的集中質(zhì)量處理，將系統(tǒng)簡化為弦-集中質(zhì)量振動體系統(tǒng)。

選用具有零浮力特性的非金屬纜繩作為拖纜，考慮到非金屬拖纜抗彎剛度很小而抗拉剛度大，近似認(rèn)為在拖纜中只產(chǎn)生拉力，不產(chǎn)生推力和彎矩；試驗(yàn)?zāi)Ｐ偷膭偠冗h(yuǎn)大于拖纜的剛度，故將模型視為剛體，據(jù)此將系統(tǒng)進(jìn)一步簡化成如圖2所示的彈性體-質(zhì)量塊系統(tǒng)。

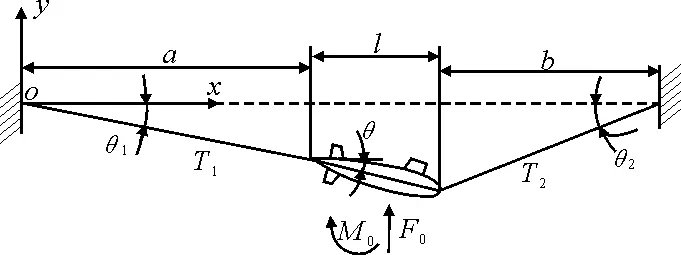
l-模型長度；a、b-模型左、右端纜長

圖2中的平面運(yùn)動系統(tǒng)有縱搖、垂蕩和縱蕩3種運(yùn)動模式，用3個獨(dú)立的參數(shù)描述模型的狀態(tài)。在如圖2所示的固定坐標(biāo)系中，試驗(yàn)?zāi)Ｐ偷臓顟B(tài)由坐標(biāo)(x，y，θ)惟一確定。

由于模型做小振幅運(yùn)動，θ、θ1、θ2是小量，近似認(rèn)為sinθ≈tanθ≈θ，sinθ1≈tanθ1≈θ1，sinθ2≈tanθ2≈θ2。近似有

(1)

由于將模型簡化為剛體，因此外界的任何擾動都可等效為通過重心的一對合力與合力矩，則試驗(yàn)?zāi)Ｐ偷拇故庍\(yùn)動方程為

θ1+T2θ2+zθ·θ=F0

(2)

式中：m——模型質(zhì)量；

y——模型重心垂向位移；

C1——水動力引起的垂蕩運(yùn)動阻尼；

T1、T2——模型左右端纜繩張緊力；

zθ——前向運(yùn)動的水動力修正系數(shù),通過模型試驗(yàn)數(shù)據(jù)庫預(yù)報；

θ——模型縱傾角；

F0——外激勵力。

試驗(yàn)?zāi)Ｐ涂v搖運(yùn)動方程為

θ-θ1)+

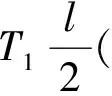
(3)

式中：J——試驗(yàn)?zāi)Ｐ偷霓D(zhuǎn)動慣量；

C2——水動力引起的縱搖運(yùn)動阻尼；

Mθ——縱搖運(yùn)動的水動力修正系數(shù)，通過模型試驗(yàn)數(shù)據(jù)庫預(yù)報得出；

M0——外激勵力矩。

模型縱向振動對其運(yùn)動安全性影響不大，可忽略縱向振動，僅考慮前向運(yùn)動，則模型的水平運(yùn)動方程為

式中：v——模型的前向運(yùn)動速度。

將θ1、θ2代入式(2)、(3)，經(jīng)整理得到模型的運(yùn)動方程。

2 系統(tǒng)固有特性計算

系統(tǒng)的3個自由度分別對應(yīng)縱蕩運(yùn)動率、垂蕩運(yùn)動率和縱搖運(yùn)動固有頻率。對本系統(tǒng)而言，只需關(guān)心其垂蕩運(yùn)動與縱搖運(yùn)動特性。當(dāng)系統(tǒng)的質(zhì)量特性與阻尼特性一定時，影響系統(tǒng)固有特性的量只有預(yù)緊力T。計算不同預(yù)緊力作用下，模型從左至右運(yùn)動時的固有頻率特性，結(jié)果見圖3。

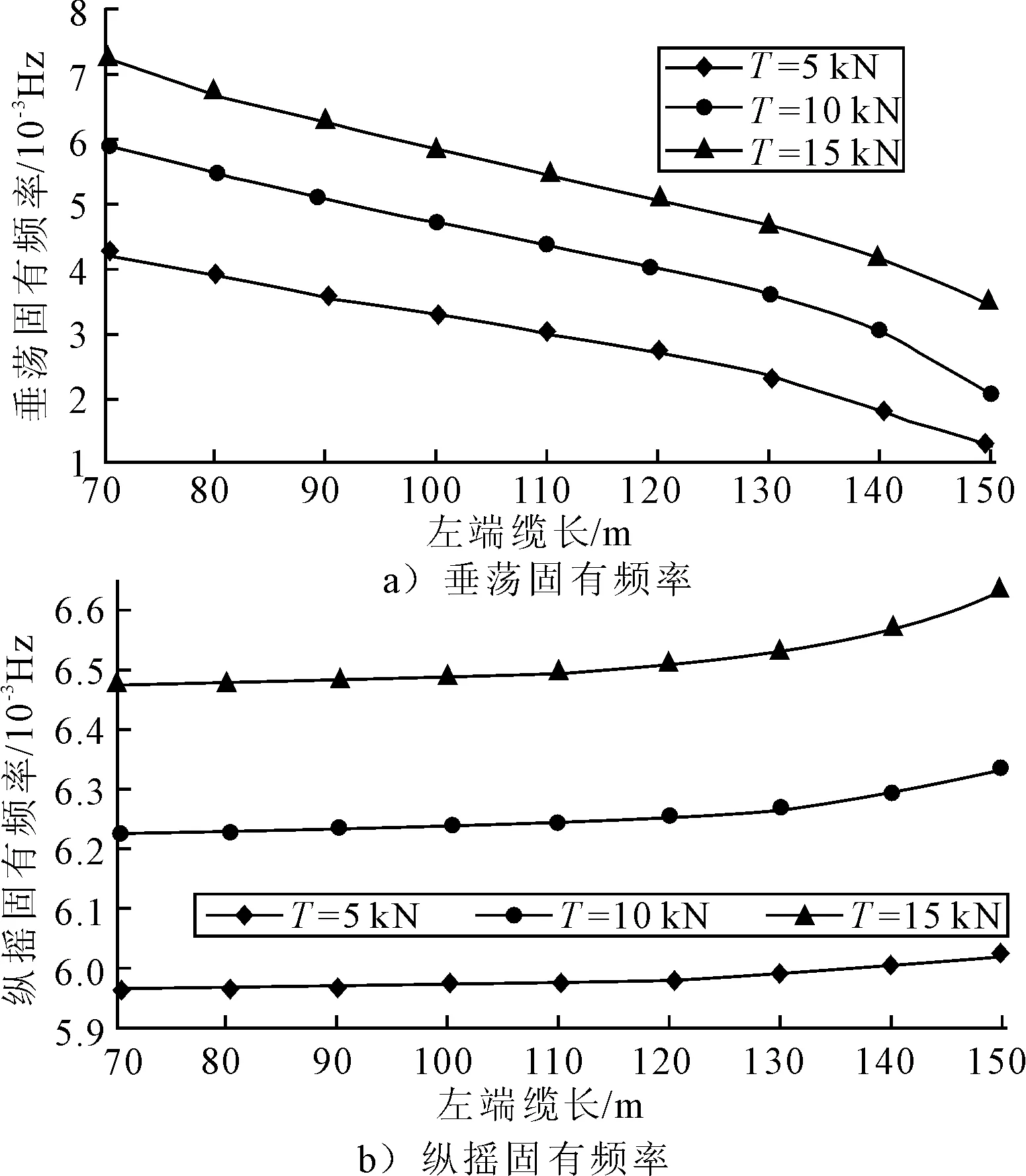
圖3 不同預(yù)緊力作用下的系統(tǒng)固有頻率

由圖3可見，模型所處的位置相同時，拖纜預(yù)緊力越大，系統(tǒng)剛度越大，其固有頻率越高。系統(tǒng)固有頻率變化規(guī)律與彈性體-質(zhì)量塊振動系統(tǒng)的一般規(guī)律是相吻合的。可以認(rèn)為本文對系統(tǒng)所作的簡化是合理可信的。模型左右運(yùn)動時，垂蕩運(yùn)動及縱搖運(yùn)動固有頻率都隨之變化，變化曲線左右不對稱，這是因?yàn)榇故庍\(yùn)動方程的修正系數(shù)zθ導(dǎo)致剛度矩陣不對稱，由此可見系統(tǒng)前向運(yùn)動對系統(tǒng)固有特性的影響不可忽視，見圖4。

圖4 典型狀態(tài)下系統(tǒng)的固有特性變化趨勢

由圖4可見，模型水平運(yùn)動對縱搖固有頻率的影響很小，而對垂蕩運(yùn)動影響較大。當(dāng)試驗(yàn)?zāi)Ｐ吞幱谒刂醒霑r，其固有特性具有典型性，可將

此作為一個典型狀態(tài)，計算不同預(yù)緊力作用下系統(tǒng)的固有特性變化規(guī)律。從圖4可以看出，系統(tǒng)的固有頻率都隨拖纜預(yù)緊力的增大而增大，呈近似線性的關(guān)系變化。當(dāng)拖纜的預(yù)緊力T在10～100 kN范圍內(nèi)變化時，系統(tǒng)的垂蕩固有頻率在0.005～0.016 Hz范圍內(nèi)變化，縱搖固有周期在0.062～0.097 Hz范圍內(nèi)變化。

3 預(yù)緊力影響與分析

假定系統(tǒng)在運(yùn)動初始時刻受到某一未知外力的干擾，產(chǎn)生某一初始偏差，計算系統(tǒng)在不同預(yù)緊力作用下的系統(tǒng)響應(yīng)。仍以4 m/s向前運(yùn)動的典型工況為例，假定四種典型的初始狀態(tài)：①初始重心位移0.1 m；②初始垂向速度0.1 m/s；③初始縱傾角1°；④初始縱搖角速度1 °/s。計算不同預(yù)緊力作用下的重心垂向位移和縱傾角響應(yīng)，結(jié)果見圖5～8。

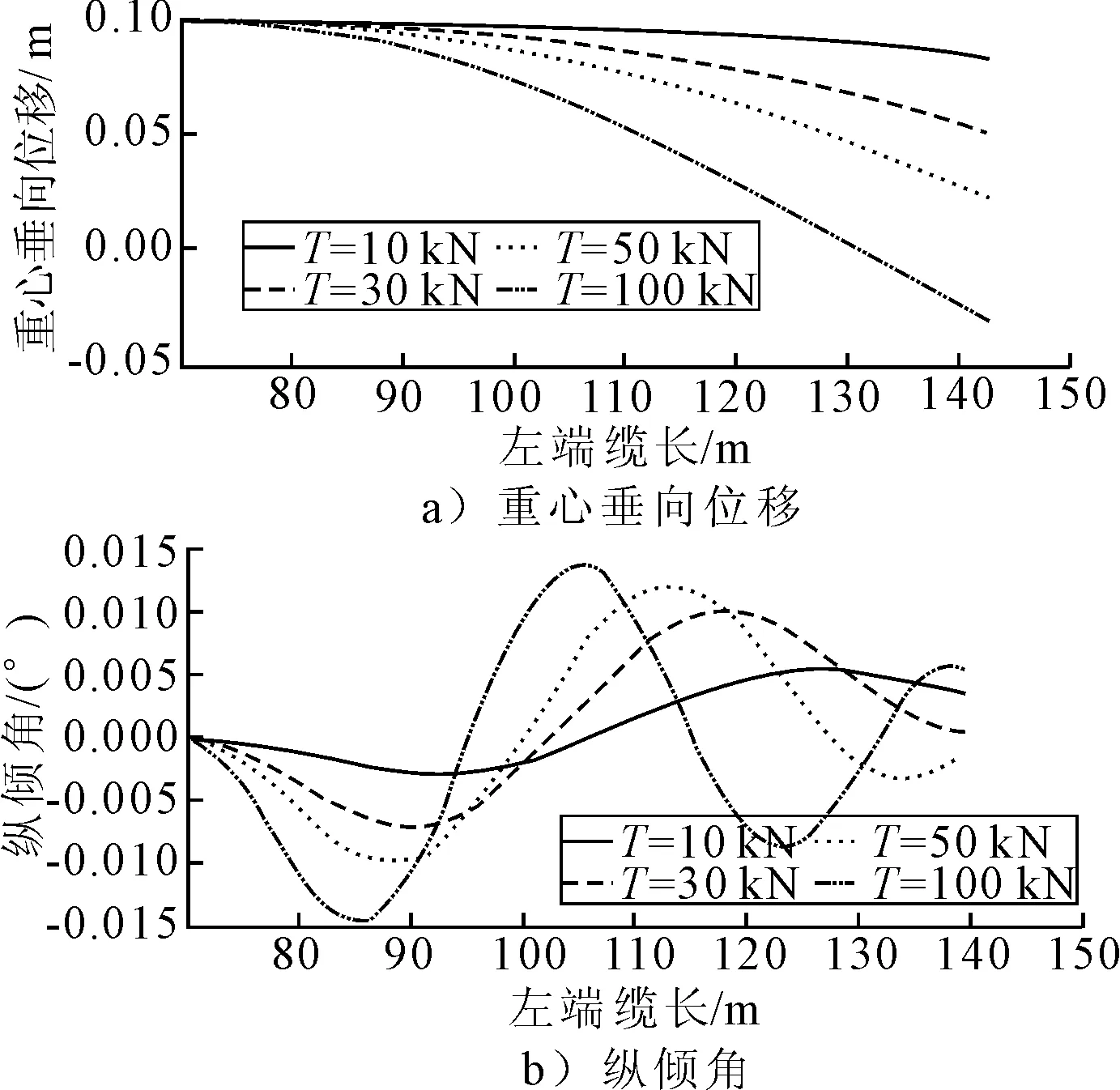
圖5 初始位移為0.1 m時系統(tǒng)的運(yùn)動響應(yīng)

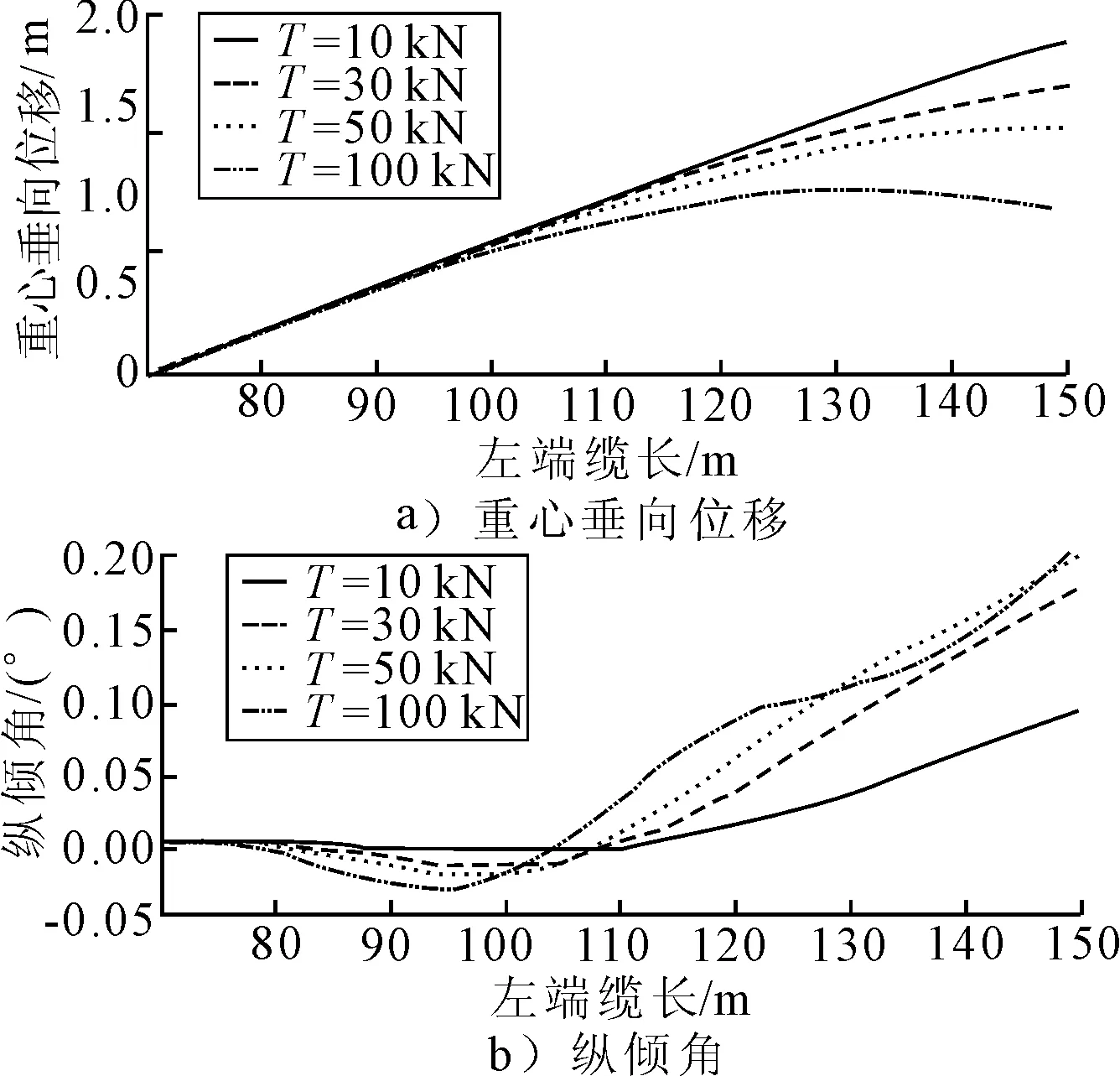
圖6 初始垂向速度為0.1 m/s時系統(tǒng)的運(yùn)動響應(yīng)

從計算結(jié)果可以看出，模型垂蕩運(yùn)動與縱搖運(yùn)動之間的耦合度很小，即初始重心位移、初始垂蕩速度不會造成較大的縱搖響應(yīng)；初始縱傾、初始縱搖角速度會造成微小的垂蕩響應(yīng)，但絕對值不是很大。預(yù)緊力越大，重心、縱傾角的最大超調(diào)量越小，重心、縱傾角向初始位置收斂的速度越快，但縱傾角呈現(xiàn)一定的振蕩。究其原因，當(dāng)預(yù)緊力T在10～100 kN范圍內(nèi)變化時，垂蕩固有周與縱搖固有周期分別在約60～200 s、10～20 s范圍內(nèi)變化，運(yùn)動時間與縱搖固有周期在同一量級，因此縱傾呈現(xiàn)振蕩。過小的預(yù)緊力會使得系統(tǒng)的剛度較小，模型偏離初始位置的距離太大，過大的預(yù)緊力則會導(dǎo)致縱傾角的振蕩，造成運(yùn)動不平穩(wěn)。因此拖纜預(yù)緊力的選取應(yīng)考慮使得模型在勻速試驗(yàn)段內(nèi)盡量平穩(wěn)運(yùn)行，且不至于產(chǎn)生過大的超調(diào)量。

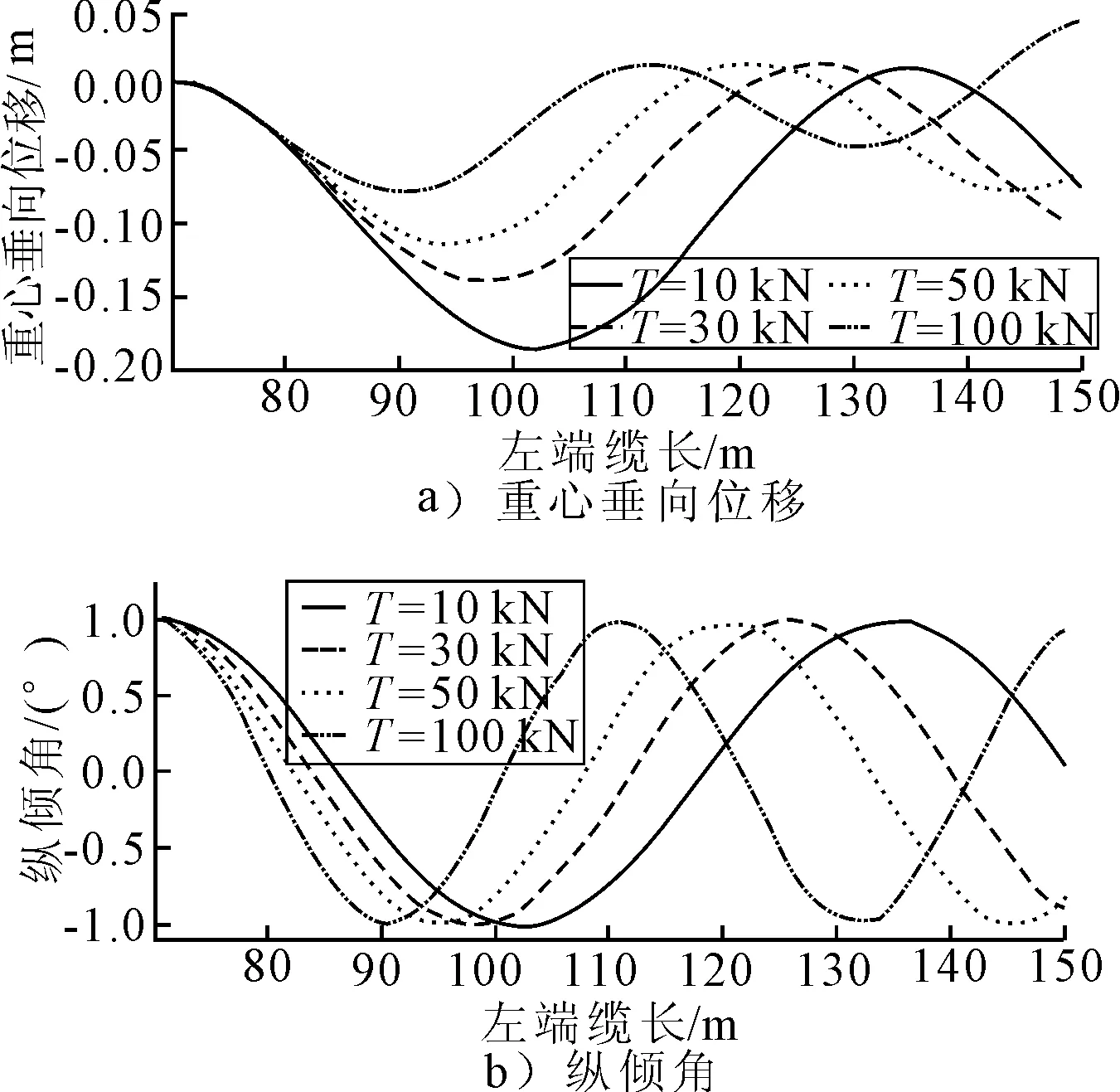
圖7 初始縱傾角為1°時系統(tǒng)的運(yùn)動響應(yīng)

圖8 初始縱搖角速度為1 (°)/s時系統(tǒng)的運(yùn)動響應(yīng)

當(dāng)預(yù)緊力T=50 kN時，模型重心位移與縱傾角的最大超調(diào)量均較小，運(yùn)動較為平緩。因此設(shè)定拖纜的預(yù)緊力為50 kN。運(yùn)用同樣的方法評估其它試驗(yàn)航速下的系統(tǒng)運(yùn)動特性，確定合適的預(yù)緊力。文獻(xiàn)[5]基于試驗(yàn)結(jié)果給出了不同航速下拖纜預(yù)緊力的建議值(見表1)，可看出，本文的計算結(jié)果與文獻(xiàn)[5]給出的結(jié)果相比稍偏大，但趨勢一致，認(rèn)為本文的計算具有較高的可信度。

4 操舵工況下的系統(tǒng)運(yùn)動響應(yīng)分析

大尺度水下綜合試驗(yàn)?zāi)Ｐ驮谶M(jìn)行試驗(yàn)研究時，有兩種典型工況：①在整個勻速試驗(yàn)段舵保持某一舵角固定不變，在這種工況下激勵力和激勵力矩都是恒定值；②持續(xù)不斷地進(jìn)行正弦操舵，在這種工況下激勵力和激勵力矩都呈正弦變化。有必要對其運(yùn)動特性進(jìn)行計算校核，以保證模型運(yùn)動穩(wěn)定性與安全性。由于試驗(yàn)?zāi)Ｐ鸵? m/s速度向前運(yùn)動是主要試驗(yàn)工況，因此仍然以此工況為例計算試驗(yàn)?zāi)Ｐ偷倪\(yùn)動特性。

表1 不同航速下拖纜預(yù)緊力建議值對比

4.1 恒定舵角工況

試驗(yàn)?zāi)Ｐ汪荷刀娑婷娣eA=2 m2，展弦比λ=2.08，翼剖面為NACA0018，求得舵角30°時激勵力的最大值：F0=11.2 kN，M0=112 kN·m。計算不同大小的力和力矩作用下，系統(tǒng)的重心垂向位移和縱傾角響應(yīng)，結(jié)果見圖9。為保證試驗(yàn)?zāi)Ｐ驮囼?yàn)過程中的運(yùn)動穩(wěn)定性和安全性，應(yīng)限定該工況下舵角應(yīng)不大于15°。

圖9 恒力作用下的系統(tǒng)響應(yīng)

4.2 正弦操舵工況

正弦操舵工況下操舵造成的激勵力和激勵力矩都是正弦形式的，若忽略相位影響，則還須確定激勵頻率與幅值。忽略頻繁操舵時的記憶效應(yīng)，簡單計算激勵幅值；由振動理論可知，當(dāng)外激勵的頻率接近固有頻率，系統(tǒng)發(fā)生共振，運(yùn)動響應(yīng)較劇烈，因此激勵頻率應(yīng)落在系統(tǒng)的固有頻率附近。

1) 激勵力幅值。上節(jié)已算出舵角為30°時，舵的最大激勵力和激勵力矩分別為11.2 kN及112 kN·m，設(shè)定舵激勵力在1～11.2 kN范圍內(nèi)變化，舵激勵力矩在10～112 kN·m范圍內(nèi)變化。

2) 激勵力頻率。由圖4可知，當(dāng)拖纜預(yù)緊力為50 kN時，系統(tǒng)的垂蕩固有頻率在0.015 Hz附近變化，系統(tǒng)縱搖固有頻率在在0.08 Hz附近變化。因此，可設(shè)定計算頻率為0.01～0.30 Hz。

3) 計算結(jié)果與分析。分別計算操舵頻率在垂蕩固有頻率附近和縱搖固有頻率附近時的系統(tǒng)響應(yīng)，因其計算結(jié)果數(shù)據(jù)較多，僅列出模型在整個運(yùn)動過程中的最大重心位移和最大縱傾角響應(yīng)，結(jié)果見圖10。

由圖10可見，當(dāng)激勵力的頻率不斷變化時，系統(tǒng)的最大重心垂向位移出現(xiàn)兩個明顯的峰值，分別對應(yīng)于兩個固有頻率，對應(yīng)于垂蕩固有頻率的峰值要明顯大于對應(yīng)于縱搖固有頻率的峰值；而最大縱傾角響應(yīng)只存在一個明顯的峰值，對應(yīng)于縱搖固有頻率，這與文中得出的規(guī)律是相同的，即垂蕩運(yùn)動對縱搖運(yùn)動產(chǎn)生的影響要小于縱搖運(yùn)動對垂蕩運(yùn)動產(chǎn)生的影響。

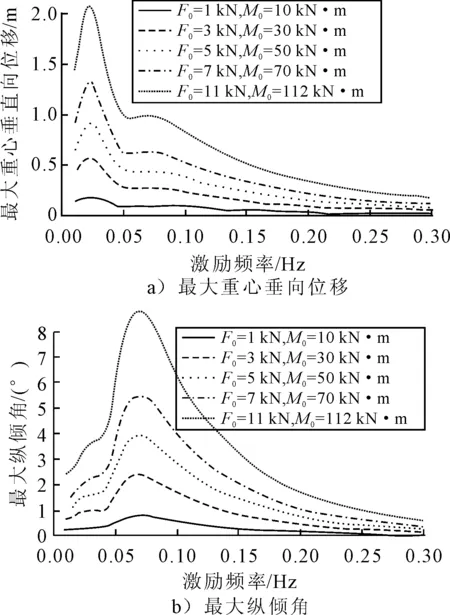
圖10 共振頻率附近系統(tǒng)的響應(yīng)

由振動的一般理論可知，當(dāng)廣義外激勵力的頻率在共振頻率附近時，系統(tǒng)的響應(yīng)將會非常大，運(yùn)動有可能會振蕩發(fā)散。但是在計算中，系統(tǒng)的響應(yīng)不是十分大，究其原因是系統(tǒng)的共振固有頻率非常小，亦即固有周期非常大，固有周期與試驗(yàn)?zāi)Ｐ拖蚯斑\(yùn)動的時間處于同一個量級，試驗(yàn)?zāi)Ｐ偷倪\(yùn)動過程只經(jīng)歷了不超過2個固有周期，系統(tǒng)的運(yùn)動發(fā)散還未來得及充分形成，整個試驗(yàn)過程便已結(jié)束。如果減小模型的速度，亦即增大系統(tǒng)的運(yùn)動時間，而保持其預(yù)緊力、激勵力不變，則系統(tǒng)又可能發(fā)生運(yùn)動發(fā)散。

用具體的算例說明這一問題。從圖11可以看出，試驗(yàn)?zāi)Ｐ偷那跋蜻\(yùn)動速度若為0.4 m/s，系統(tǒng)的運(yùn)行時間變?yōu)?00 s，整個運(yùn)動過程經(jīng)歷了約3個垂蕩固有周期或10個縱搖固有周期，振蕩已經(jīng)充分發(fā)散。事實(shí)上，系統(tǒng)產(chǎn)生大重心垂向位移和大縱傾之后，文中所作出的相關(guān)近似已不成立，系統(tǒng)的非線性效應(yīng)也會體現(xiàn)出來，實(shí)際的重心位移和縱傾角不會這么大。

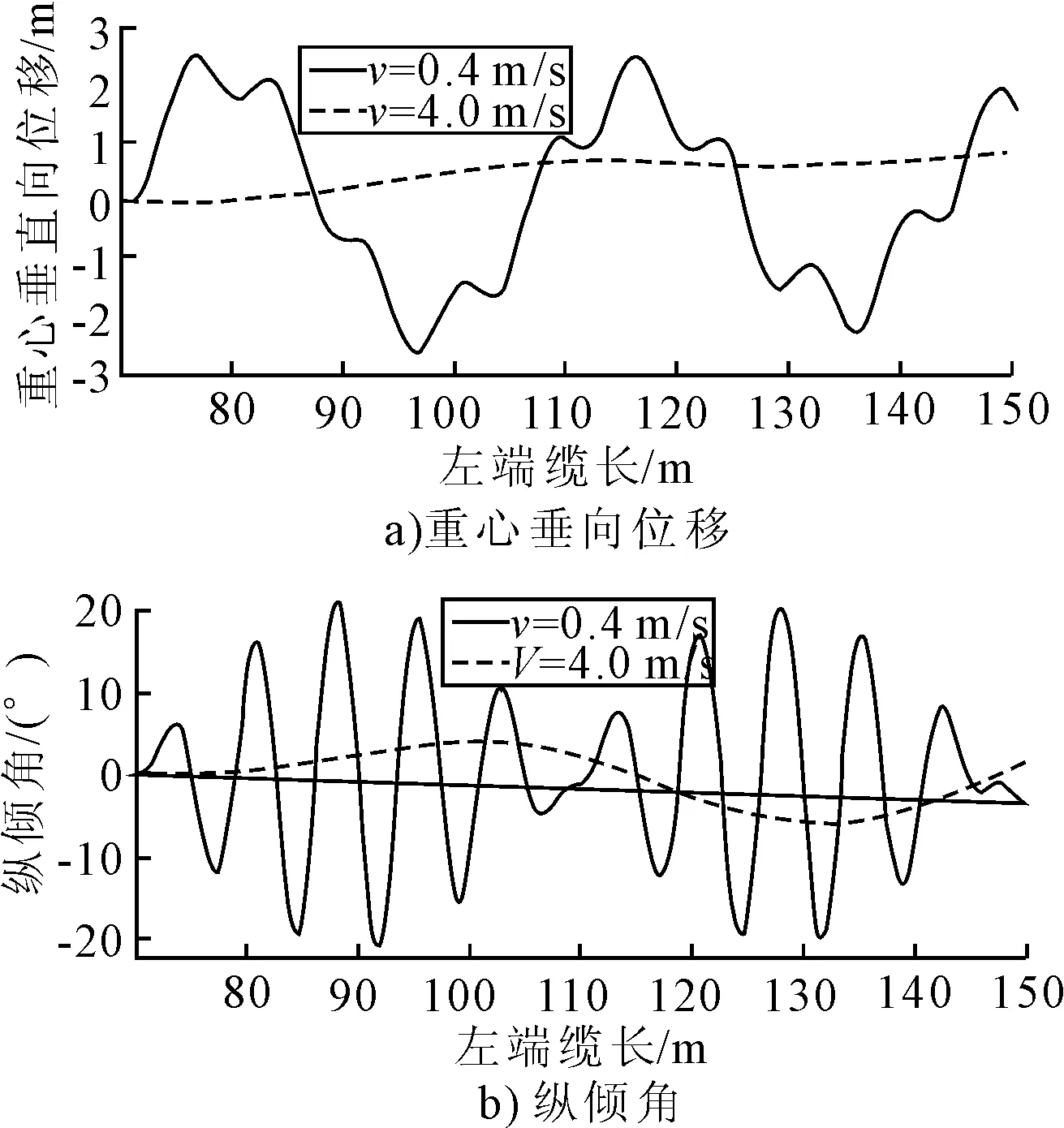
T0=50 kN；F0=11.2 kN；M0=112 kN·m；w=0.05 Hz

當(dāng)試驗(yàn)?zāi)Ｐ鸵? m/s的速度向前運(yùn)動時，在激勵力幅值不大于7 kN的條件下，模型的最大重心位移不大于1.3 m，最大縱傾角不大于6°，最大端部位移不大于1.7 m。正弦操舵工況與恒定舵角工況相比，最大舵角的限制可適當(dāng)放寬。為保證試驗(yàn)?zāi)Ｐ偷陌踩裕也俣婀r下最大舵角可適當(dāng)放寬至約18°。

當(dāng)試驗(yàn)?zāi)Ｐ鸵云渌俣认蚯斑\(yùn)動時，按表1的數(shù)值改變預(yù)緊力，可保證整個運(yùn)動過程經(jīng)歷較少的固有周期數(shù)，使共振不會充分形成、發(fā)展。并且速度降低之后，舵激勵力和激勵力矩將會急劇減小，系統(tǒng)的響應(yīng)不會很大，可以保證試驗(yàn)?zāi)Ｐ驮诓煌囼?yàn)航速下的運(yùn)動穩(wěn)定性與安全性。

5 結(jié)論

為保證試驗(yàn)?zāi)Ｐ驮囼?yàn)過程中的運(yùn)動穩(wěn)定性和安全性，應(yīng)設(shè)定恒舵角工況下舵角不宜超過15°，正弦操舵工況下舵角不宜超過18°。

[1] BYSTORM L.Simulation of submarine recovery procedures in case of flooding[C]∥ Warship 2002,International symposium on Naval submarines. London UK, 2002.

[2] 任 凱.破損艦艇拖航穩(wěn)度分析[J].船舶，2007，18(2)：16-19.

[3] 郝英澤，胡 坤，劉百順.潛艇水下破損定深操縱方法仿真研究[J].船海工程，2010，39(2)：111-113.

[4] 何春榮，趙橋生，馬向能.潛艇大攻角操縱運(yùn)動預(yù)報[J].船舶力學(xué)，2010，14(4)：340-346.

[5] 楊仁友.綜合試驗(yàn)平臺線型初步方案與纜繩載荷初步分析報告[R].無錫：中國船舶科學(xué)研究中心，2010.