基于Bayes理論的永磁無刷電機的可靠性研究
何銀光,胡小東,常榮勝
(克拉瑪依職業技術學院,新疆 獨山子,833600)
前言
永磁無刷電機具有結構簡單、速度調節能力強、功率高以及功率密度高的優勢,由于其自身強大的技術優勢使其在工業領域中得到了廣泛的應用。永磁無刷電機的可靠性評估可以有效地對永磁無刷電機進行可靠性水平的定量評價,通過可靠性分析可找出其薄弱環節,從而能夠有利于永磁無刷電機的優化設計和性能改進,進而提高其在工業領域應用的可靠性。
傳統的可靠性評估需要大量的可靠性數據,而對于永磁無刷電機,由于經濟條件和可靠性實驗的設計等原因,進行大子樣的可靠性分析比較難于實現,因此,需要需求一種可靠性評估方法進行小子樣的可靠性分析。Bayes理論是一種小子樣的可靠性評估方法,可以提高無刷永磁電機可靠性分析的效率,利用Bayes理論可以對考慮不同的實驗之前的數據信息,從而能夠提高無刷永磁電機的失效數據,進而可以提高無刷永磁電機可靠性評估的效率。
1 Bayes理論概述
設事件A和彼此不相容的m個事件E1,E2, … ,Em的一個事件,并且僅僅能和該事件同時發生,驗前概率用P(Ei)來表示。一次試驗結束以后,結果為事件B,根據Bayes條件概率可以獲得如下的條件概率表達式:

由式(1)可知,當P(Ei)和P(Ei|B)已知時,驗后概率即可求出。驗后的信息和驗前的知識、驗前的信息和驗后的信息是相互約束的。為了能夠成功地處理概率問題,應該充分地利用驗前信息為決策提供信息支持。
式(1)的隨機變量的分布形式如下所示:
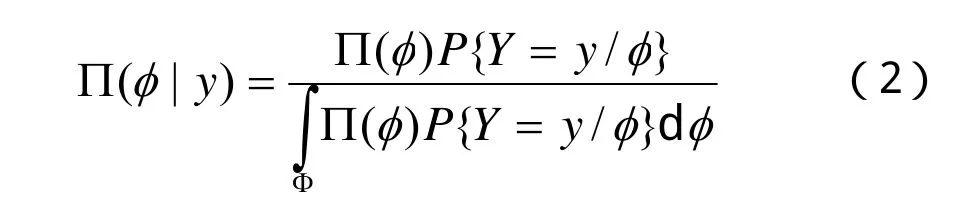
式中:Y表示離散隨機變量;φ表示未知分布參數,φ∈Φ;∏(φ)表示驗前概率密度;∏(φ|y)表示產生觀測值x后的驗后概率密度。
當Y表示連續型的隨機變量時,驗后概率密度可以表示為如下的形式:
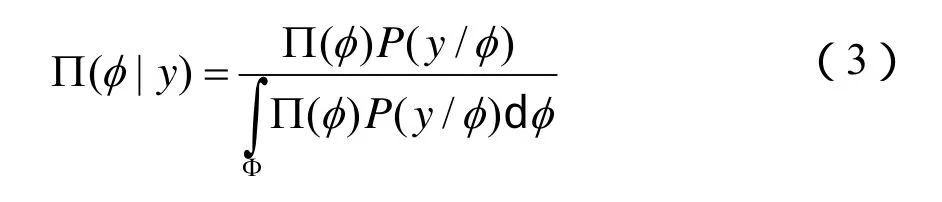
式中:P(y/φ)表示在φ下Y的條件概率密度函數。
進行m次試驗,可以獲得子樣Y=(Y1,Y2, …,Ym),進而可以獲得φ在給定Y下的驗后分布,相應的驗后概率分布密度可以表示為如下的形式:
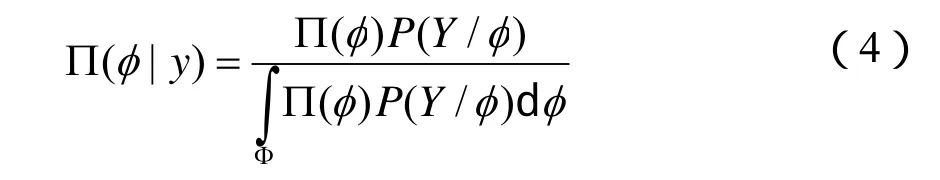
式中:Φ表示參數集;P(Y/)φ表示相應的聯合概率密度函數。
經過試驗之后,在∏(φ|y)中包括所有的關于φ的信息,根據 Bayes理論,以∏(φ|y)為先驗的φ統計推斷可以表示為如下的形式:

2 Weibull分布下永磁無刷電機的Bayes理論模型
(1)基于Bayes理論永磁無刷電機可靠性分析的思路
Weibull分布可以表達為不同的形狀,并且能夠適應多種試驗數據。設永磁無刷電機的壽命服從Weibull分布W(n,)σ,相應的分布函數可以表示為如下的形式:
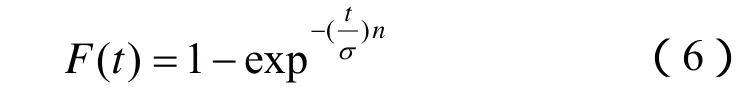
式中:n表示形狀因子,n>0;σ表示特征壽命,σ> 0。
從m個定時截尾時刻t1<t2<…<tm得到m組實驗數據,在ti時刻檢測qi個永磁無刷電機樣本,如果全部的永磁無刷電機不失效,則可以得到一組無失效的數據(ti,ri) ,ri表示在ti時正在進行的檢測的永磁無刷電機樣本,ri=q1+q2+…+qm。
永磁無刷電機可靠性分析的基本思路如下:
(a)建立永磁無刷電機失效率的先驗分布。
(b)建立先驗分布超參數分布,利用Bayes理論,進行失效率的點估計。
(c)利用配分布曲線法進行永磁無刷電機的參數估計。
(2)可靠性參數的估計
設永磁無刷電機在ti時刻的失效概率為λi,可以表示為如下的形式:

以Beta分布為失效概率λi的先驗分布,相應的表達式如下所示:
式中:B(l,k)表示Beta分布函數,l和k表示超因子,均為不為零的正值。根據Beta分布函數的特點,確定l和k的取值范圍為l≤1,k≥1,然后進行下一步的先驗,對應的表達式可以表示為如下的形式:
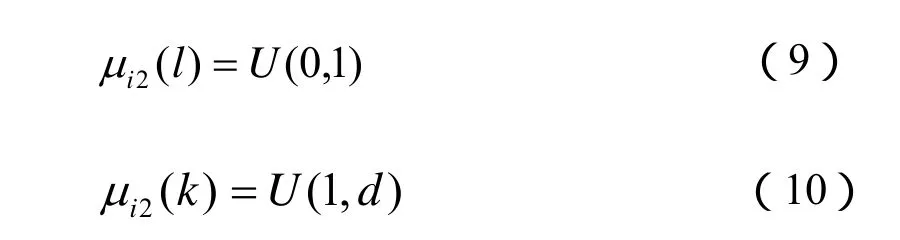
式中:l和k相互獨立,d不應該過高,從而能夠防止λi的先驗密度尾巴過細,能夠保證Bayes估計的魯棒性,根據永磁無刷電機可靠性分析的實際,定義c=6-7。進而,λi的先驗分布可以表示為如下的形式:
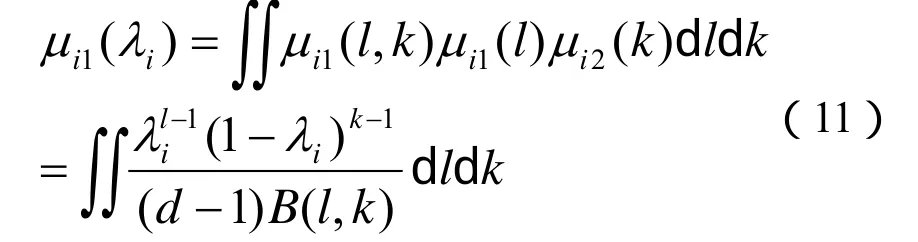
利用 Bayes理論將先驗和似然函數聯系起來獲得λi的后驗分布,后驗均值對λi進行估計,可以表示為如下的形式:
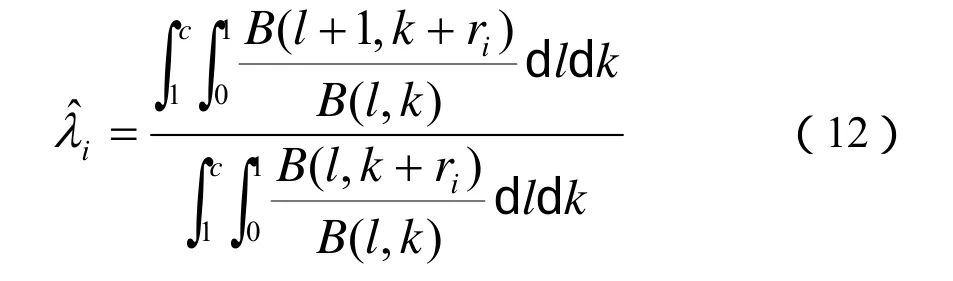
利用相同的步驟,可以獲得λi-1,λi-2,…,λ1先驗分布的點估計,然后,根據配分布曲線法獲得永磁無刷電機的可靠性參數估計。
3 永磁無刷電機的可靠性試驗
永磁無刷電機可靠性試驗設計如下:在可靠性試驗過程中,永磁無刷電機是可修復系統,當其發生失效時立即進行修復,并且將試驗時間和失效次數記錄下來,可靠性試驗采取了截尾試驗,在150h,200h,250h,300h,350h,400h,450h,500h 進行記錄,并且撰寫可靠性試驗數據測試報告,永磁無刷電機可靠性試驗的數據統計結果見表1所示。

表1 永磁無刷電機可靠性試驗的數據統計結果
利用表1中的可靠性試驗數據,可以對永磁無刷電機進行可靠性估計。利用公式(12)和配線分布法可以獲得永磁無刷電機可靠度的估計結果,見表2。
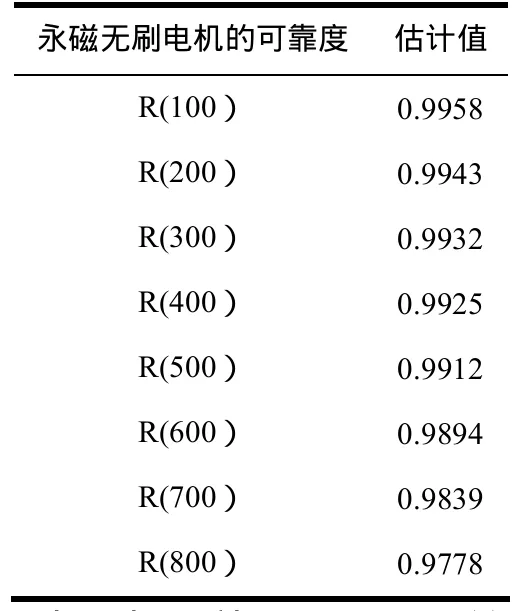
表2 永磁無刷電機可靠度的估計結果
從表2可以看出,利用Bayes理論對永磁無刷電機進行可靠性研究具有較好的優越性,使可靠性評估無需大量的試驗數據,能夠有效地解決在進行可靠性評估的過程中由于樣本少而帶來的參數估計不精確的問題,具有較好的預計性,該方法可以為永磁無刷電機故障提供參考范圍,從而能夠防止永磁無刷電機在故障的高發區運行。
4 結論
對于永磁無刷電機,其可靠性試驗存在數據樣本少、試驗成本高、無法進行大樣本、長周期的可靠性試驗的缺點。因此,本文利用 Bayes理論建立可靠性估計模型并設計出永磁無刷電機的小樣本截尾試驗,充分地利用驗前數據,獲得了可靠性特性參數的估計。利用 Bayes理論可以在已知非常少的實驗數據樣本的情況下,利用截尾實驗,并且根據驗前信息能夠獲得永磁無刷直流電機可靠度的非常充分的估計值。
[1]賈亞洲.數控系統可靠性國內外現狀及對策[J].中國制造業信息化,2006(6):51-53.
[2]徐廷學,甄偉,陳紅,等. 基于 Bayes 理論的導彈貯存可靠性試驗研究[J].海軍航空工程學院學報, 2006(6):672-674.
[3]李承劍,慕曉冬,張華鵬. 基于 Bayes理論的航空電子設備可靠性評估[J].火力與指揮控制,2009(1):139-141.
[4]金少華.無失效數據的Bayes分析[J].低壓電器,2006(7):3-5.

