纖維增強聚合物加速老化壽命預測方法研究進展

樊 威，李嘉祿

(1.天津工業大學，天津 300160；2.天津市和教育部共建先進紡織復合材料重點實驗室，天津 300160)

纖維增強聚合物(FRP)因其比強度、比模量高, 抗疲勞性、耐腐蝕性突出, 減震能力強, 耐高溫性能好,破損安全性好和可設計性強等優點,而被廣泛應用于航空、海事、交通、基礎設施以及消費品等工業領域[1]。但是, 由于聚合物在熱、濕、紫外光、鹽霧與風沙等環境因素作用下會發生老化, 使得設計與使用部門對FRP復合材料結構的壽命預測分外關注。

經過幾十年的研究發現，FRP材料的自然老化是一個非常復雜的問題，原因是FRP材料與金屬材料相比，其本身的物理、力學性能存在較大的分散性，導致在老化試驗過程中需要用大量的試樣，試驗費用非常高，在項目研究中難以承受, 因此在實際工程應用中，需要在自然老化數據少、老化周期短的情況下對復合材料壽命進行預測，根據描述老化過程的出發點與描述參數的不同，壽命預測方法可歸結為3大類[2]：(1)剩余強度模型；(2)老化動力學模型；(3)應力松弛時間模型。

1 剩余強度模型

Γ·Μ·古尼耶夫[3]等人認為，對于無負荷條件下暴露于環境中的熱固性復合材料,假設增強過程和損傷是相互獨立的, 那么性能的不可逆變化所造成的復合材料強度變化可用式(1)描述：

S=S0+η(1-e-λt)-βln(1+t)

(1)

式中：S—復合材料老化t小時后的強度；S0—復合材料初始強度；η—材料固化程度參數；λ—材料和外部環境參數；t—老化時間；β—材料抵抗裂紋擴展能力參數；—外部環境侵蝕性參數。

η和β僅與材料特性有關, 可經一系列人工氣候老化試驗來確定,而且可用于確定公式(1)中的參數，并外推到自然環境。葉宏軍[4]等用公式(1)預測T300/ 4211復合材料層壓板在濕熱環境下的強度變化,與實測值有較好的一致性。肇研等[5]在式(1)的基礎上,用中值老化方程的回歸分析方法確定了具有高置信度、高可靠度的復合材料老化公式:

SR=S0+η(1-e-λt)-βln(1+t)-kR(t)σ

(2)

式中：SR是置信度為γ、可靠度為R的老化剩余強度；待定系數S0、η、λ、β、含義與式(1)相同，kR(t)是置信度為γ、可靠度為R的二維單側容限系數，σ是老化剩余強度的標準差。

除了以上兩種常用的剩余強度預測模型外，常新龍[6]應用橋聯模型計算了玻璃纖維/環氧樹脂復合材料的吸濕老化剩余強度, 計算結果與試驗結果一致。李暉等[7]基于二元統計分析方法，建立GF增強復合材料在老化過程中彎曲強度與老化時間、環境綜合因子之間的二元一次方程，通過計算可得方程的形式y= 684.13-4.071t-0.025w，其中環境綜合因子w 是一個和溫度(T)濕度(H)及光照輻射量(Q)3個因素相關的函數，即w= f (T，H，Q)。利用6個地區3a試樣的試驗數據對方程進行驗證，結果預測值和實測值有很好的吻合性。

2 老化動力學模型

Dakin[8]認為在一定老化溫度下,材料性能殘余值p與老化時間t有如下關系:

F(p)= Kt

(3)

式中：K為反應速率常數，再結合阿累尼烏斯(Arrhe-nius)公式：

K=A0exp(-E/(RT))

(4)

式中：A0為前因子；E為活化能；R為氣體常數；T為熱力學溫度。推出線性關系動力學模型：

lgt=lg(f(pe)A0)+E/(2.303RT)=a+bT-1

(5)

此式即著名的Dakin壽命方程。卜樂[9]等用公式(5)預測了冷卻塔拉擠成型玻璃鋼托架的濕熱老化性能及使用壽命，得到各試樣在水溫28℃可有30年或更長時間使用壽命的結論。直線法在原理上簡單明了，但是應用條件比較苛刻，因為此法要求每一老化溫度T下的變化均需正好達到臨界值pe才能進行回歸處理，這不僅延長了試驗時間，而且不易準確表現性能隨時間的變化關系。針對直線法的缺點，有研究者提出動力學曲線直線化模型和作圖法，但均難得到理想的壽命預測模型。蘆艾[10]指出，較晚出現的數學模型法綜合了直線法、動力學曲線直線化法和作圖法的優點，是目前既可靠又可行的材料性能變化預測方法。

目前也有人用差示掃描量熱法和熱重分析方法研究復合材料的熱解動力學并進行使用壽命的預測[11]。

3 應力松弛時間模型

所謂松弛過程是指高聚物在外場作用下，通過分子運動從一種平衡狀態過渡到與外場相適應的新的平衡狀態。完成此過程所需的時間稱為松弛時間。松弛時間模型認為，材料的松弛時間依賴于環境因素，老化時間到達松弛時間τ時， 材料喪失使用性能。Wiederhorn[12]根據大量的試驗結果給出了玻璃纖維復合材料在濕度和應力2種環境因素協同作用下腐蝕速率v的經驗公式：

v=axfexp[-E/(RT)]exp[bk/(RT)]

(6)

式中：x為相對濕度；f為材料與環境介質之間的相互作用參數；E為不受外力時材料的內聚能，J/cm3；R為氣體常數；T為熱力學溫度，K；k為應力因素；a,b為常數；上式變形可得Wiederhorn腐蝕壽命公式：

t = ax-fexp[E/ (RT)]exp[-bk/ (RT)]

(7)

劉觀政[13]等在Wiederhorn腐蝕壽命公式的基礎上結合玻璃態高聚物大應力作用下松弛時間與應力之間關系式，分離濕度與應力，得出純濕度對材料腐蝕壽命τ的影響：

τ=ax-f

(8)

式中a為常數。根據橡膠彈性理論，橡膠溶脹理論并結合應力松弛時間公式，推導出純溶脹對材料腐蝕壽命的影響：

(9)

式中：τ為溶脹后應力松弛時間；τ0為溶脹前應力松弛時間；V2為溶脹后高分子體積膨脹率。考慮時間因素并結合高聚物自由體積膨脹理論、Arrhe-nius規律推導出純溫度對腐蝕壽命影響：

(10)

綜合式(8)、(9)、(10)， 得出溶脹體積變化率的應力松弛時間模型：

τ=

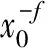
(11)

B為常數。該模型在腐蝕動力學方程和Wiederhorn經驗公式的基礎上,結合橡膠彈性理論、自由體積膨脹理論和應力松弛等基礎理論,以及Arrhe-nius規律和Fick擴散定律,較系統地解釋了溫度、濕度、水和應力4個環境因素對高聚物及其復合材料的腐蝕作用規律。但由于模型是將溫度、濕度、應力、溶脹諸因素對老化壽命的影響簡單疊加后得到，未考慮各因素間的相關性，因而具有一定的局限性。

4 展望

FRP復合材料加速老化壽命預測方法的研究已取得了很大的進展, 但其在指導實際工程應用方面發揮重大作用還有待進一步深入研究。其中最突出的問題就是如何在盡量短的時間內全面地、合理地評估復合材料的使用性能及工作壽命，為此提出以下一些展望:

(1)長期自然環境中的耐久性試驗數據較少,人工快速老化和自然老化試驗結果的對應關系也更為少見, 因此缺乏FRP復合材料在典型環境下快速試驗與自然老化試驗的同步和系統研究,從而對所建立的FRP復合材料耐久性評價體系和預測模型缺乏驗證依據;

(2)建立能合理地反映材料真實使用情況下的老化壽命預測模型，及對FRP復合材料在多種環境耦合條件下以及受力狀態與環境條件的耦合狀態下的老化壽命預測模型;

(3)拓寬計算機在復合材料老化研究中的應用, 開發相應的計算機模擬軟件，用計算機預測復合材料的使用壽命。

參考文獻：

[1]M K Bannister.Development and application of advanced textile composites[J].Materials Design and Applications,2004,22(4):253—260.

[2]陳躍良,劉旭.聚合物基復合材料老化性能研究進展[J]. 裝備環境工程, 2010,7(4):48—56.

[3]Bulmanis V N, Gunyaev G M, Kriv onos V V. RISA SPAVLAM [M]. Moscow: USSR, 1991.

[4]葉宏軍,詹美珍.T300/4211復合材料的使用壽命評估[J].材料工程,1995，(10):3—5.

[5]肇研,梁朝虎.聚合物基復合材料自然老化壽命預測方法[J].航空材料學報, 2001,(2):55—58.

[6]常新龍,李正亮,胡寬，等.應用橋聯模型預測復合材料吸濕老化剩余強度[J].復合材料學報，2010,27(6):208—212.

[7]李暉,張錄平,孫巖，等.玻璃纖維增強復合材料的壽命預測[J].工程塑料應用，2011,39(1):68—73.

[8]李余增.熱分析[M].北京：清華大學出版社,1978.

[9]卜樂宏,呂爭青.拉擠成型玻璃鋼托架的濕熱老化性能及使用壽命[J].上海第二工業大學學報,2007,24(2):117—124.

[10]蘆艾,王建華.高分子材料庫存條件下性能變化研究法[J].四川化工與腐蝕控制,2000,3(4):34—37.

[11]石拓. PC/CaCO3/NBR復合材料熱解動力學及壽命預測[J].材料工程,1993,(11):14.

[12]WIEDERHORN S W. An Error Analysis of Failure Prediction Techniques Derived from Fracture Mechanics[J].Journal of the American Ceramic，1976，(32)：403—411.

[13]劉觀政,張東興,呂海寶，等.復合材料的腐蝕壽命預測模型[J].纖維復合材料,2007,(1):34—36.