連續(xù)小波變換在探地雷達信號分析中的應(yīng)用研究

黃 敏，朱德兵，郭政學，王樹敏

（1.河南省煤田地質(zhì)局 物探測量隊，河南 鄭州 450009；2.中南大學 地球科學與信息物理學院，湖南 長沙 410083）

連續(xù)小波變換在探地雷達信號分析中的應(yīng)用研究

黃 敏1，朱德兵2，郭政學1，王樹敏1

（1.河南省煤田地質(zhì)局 物探測量隊，河南 鄭州 450009；2.中南大學 地球科學與信息物理學院，湖南 長沙 410083）

廣泛應(yīng)用于工程勘探的探地雷達，由于其發(fā)射的高頻電磁波在介質(zhì)中迅速衰減、受環(huán)境噪聲大等因素影響，探測剖面難以對相對較深的異常體有較好的響應(yīng)。復信號分析提取三瞬參數(shù)可多角度分析信號，并能突出弱反射信息，但易受噪聲干擾，且常規(guī)的濾波方法不能有效地去除這一干擾。將具有時～頻雙重局限性的小波變換引入到復信號分析中，解決了復信號分析易受噪聲干擾的問題，恢復了其對異常提取的能力。將此算法用于實際雷達探測數(shù)據(jù)處理中，取得了良好的應(yīng)用效果。

連續(xù)小波變換；復信號分析；探地雷達；異常提取

0 前言

探地雷達具有輕便靈活，適應(yīng)性強，工作效率高，無損、分辨率高等諸多優(yōu)點，在淺層地球物理勘探中有著廣泛的應(yīng)用［1］。探地雷達數(shù)據(jù)剖面直觀，在信噪比較高、探測效果較好的情況下，能直接根據(jù)原始剖面進行解釋、解譯。但在大多數(shù)情況下，環(huán)境噪聲大，淺層干擾嚴重，地質(zhì)結(jié)構(gòu)復雜或者所需探測深度較大，剖面往往不能直觀解釋。并且由于雷達發(fā)射的高頻電磁波在介質(zhì)中傳播時衰減迅速，造成利用所接收的弱反射電磁波信號解釋困難。所以怎樣從復雜的原始數(shù)據(jù)剖面中提取弱反射信號，進行圖像解譯和異常分析對雷達資料的解釋尤為重要。許多學者進行過相關(guān)的研究，柳剛等人［2～5］研究過小波變換在信號去噪和弱信號提取上的應(yīng)用，但所用的都是離散小波變換，分解和重構(gòu)較為粗糙。張英德等人［6～8］采用 Hilbert－Huang變換對信號進行分析和處理，但其存在瞬時頻率波動，嚴重時還會出現(xiàn)附加的虛假成份，對信號的最高分析頻率只能達到采樣頻率的1／4以下，信號的分析受到了限制［9］。

1 小波復信號分析弱信號提取的理論基礎(chǔ)

1.1 相位、頻率分析法的優(yōu)勢

球面電磁波在均勻介質(zhì)中傳播可用式（1）表示［10］。

其中 E0為天線的初始輻射電場強度；φ0為初始相位；波數(shù)k＝α＋jβ；α為相位常數(shù)；β為衰減系數(shù)。

此時電磁場的相位表示為式（2）。

φ1＝ω0t＋φ0＋αr （2）

當?shù)叵麓嬖诜瓷湎禂?shù)為R的反射體時，其反射的電磁波表示為式（3）。

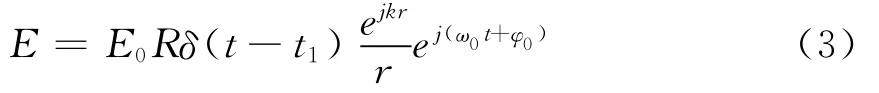
這時反射電磁波的相位為式（4）。

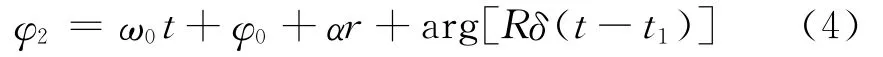
對比式（2）和式（4）可以得出這樣的結(jié)論：

（1）當存在異常體反射時，其電磁波的相位會引入由異常體產(chǎn)生的相移arg［Rδ（t－t1）］。

（2）角頻率為相位的導數(shù)，同樣由于異常體的引入，會產(chǎn)生arg′［Rδ（t－t1）］／2π的頻移。

由于信號的相位、頻率均與振幅無關(guān)，因此對信號的相位分析、頻率分析可以同等大小來反映異常體反射信號，能更好地從弱反射信號中提取出相應(yīng)的地質(zhì)信息，這是振幅分析所不能比擬的。

1.2 探地雷達數(shù)據(jù)的復信號分析

由于相位、頻率分析法在弱信號提取上具有優(yōu)勢，提取信號中的相位、頻率信息能更好地對雷達記錄做出正確的解譯。復信號分析能分離信號中的振幅、相位信息。

探地雷達系統(tǒng)中的反射信號可由式（5）表示［11］：

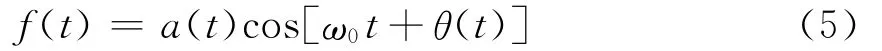
a（t）為信號的包絡(luò)，其頻帶寬度Δω遠小于ω0，一般我們認為雷達反射信號f（t）為窄帶信號。f（t）的希爾伯特變換）如式（6）表達：

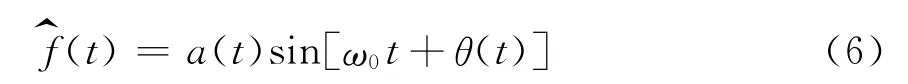
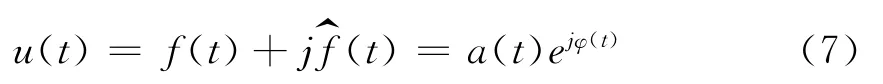
其中 φ（t）＝ω0t＋θ（t）。

從式（7）中可以得到分析信號的三瞬參數(shù)：瞬時振幅a（t），瞬時相位φ（t）及其導數(shù)瞬時角頻率ω（t），分別如式（8）、式（9）、式（10）所示。

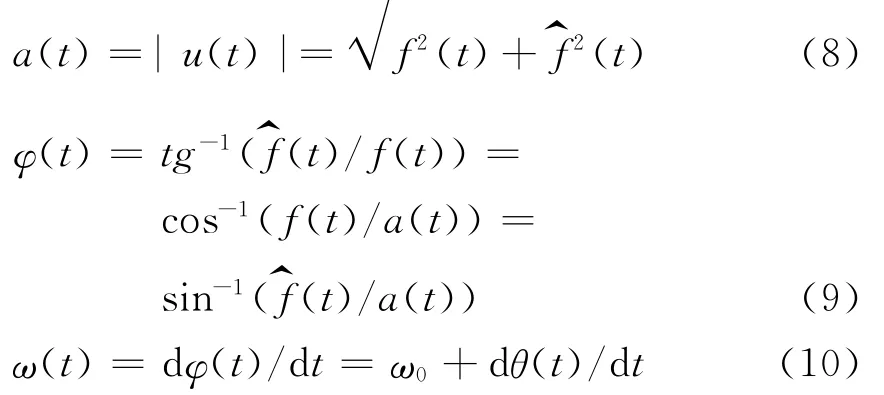
在許多文獻［6、12、13］中，都將瞬時相位表示為：，其主值范圍為（－π／2，π／2）。實際情況下f（t）取值可以為零，但在計算和成圖時，要求f（t）≠0，這就造成相位－π／2和π／2的缺失；在過f（t）取值為零的點時，出現(xiàn)相位的跳變，并在求導計算瞬時頻率時，出現(xiàn)尖峰脈沖。因此用該式表示相位所計算出的瞬時相位剖面和雷達記錄剖面，不能保持良好的對應(yīng)關(guān)系，且使瞬時頻率剖面分辨率極低。由于反正弦和反余弦函數(shù)不存在這樣的問題，用其表達瞬時相位優(yōu)于反正切。用反余弦函數(shù)表示相位時，為使其取值和成圖時與原始雷達記錄剖面保持一致，將其相移π／2，使其取值區(qū)間為 ［－π／2，π／2］，其表達式為：

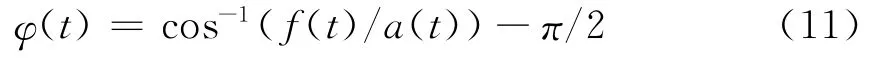
圖1（a）和（b）分別展示的是200MHz天線正對鋁板，前后移動范圍為1m～23m時，對采集的數(shù)據(jù)采用反正切和反正弦表達式所計算出的瞬時相位剖面圖。可以看出，采用反正切計算出來的瞬時相位剖面，不如反正弦計算出來的對弱反射信息的反映效果好。

下頁圖2中的（a）和（b）分別展示了對用反正切和反正弦表達式求取瞬時相位求導而計算出的單道瞬時頻率的對比圖。同樣可看出，由反正切計算的瞬時相位求導得到的瞬時頻率，由于相位的突變而出現(xiàn)大量的尖峰脈沖，這使得利用瞬時頻率剖面對探測數(shù)據(jù)進行解釋變得極為困難。

圖1 計算瞬時相位剖面Fig.1 Arctangent（a）and arcsine（b）calculate the instantaneous phase profile

在對信號進行復信號分析過程中，信號中的噪聲也被放大，使得多參數(shù)信息受噪聲干擾嚴重，這給信號多參數(shù)分析帶來了困難，甚至對數(shù)據(jù)的解釋和判讀還不如原始信號。復信號分析方法的這種缺陷限制了其應(yīng)用范圍。圖2 計算單道瞬時頻率Fig.2 Arctangent（a）and arcsine（b）calculate the instantaneous frequency of single－channel

1.3 探地雷達數(shù)據(jù)的小波復信號分析

1992年 Mallat提出李氏（Lipschitz）常數(shù)，可以用來衡量信號的奇異性［15］，并證明通過某點小波變換的極大模可以求取此點的李氏常數(shù)。若某點x0的李氏常數(shù)為a，當｜x－x0｜＜δ時，δ為任意的正實數(shù)，函數(shù)f（x）的小波變換滿足｜Wsf（x）｜≤ksa，其中k為正實數(shù)，s為小波變換的尺度。信號的李氏常數(shù)取值區(qū)間為［0，1］，因而信號的小波變換的極大模將隨尺度s的增加而增大；相反的，噪聲的李氏常數(shù)小于零，噪聲的小波變換的極大模將隨尺度s的增加而減小。現(xiàn)證明隨機噪聲的李氏常數(shù)a為負數(shù)。

設(shè)n1（x）為隨機噪聲，其方差為σ2，則：

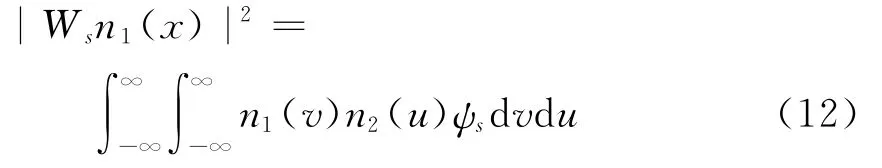
其中 ψs＝ψs（x－v）ψs（x－u）。

那么 E（｜Wsn1（x）｜2）＝ ‖ψ‖2σ2／s，其中E（·）表示求其期望，‖·‖表示求其L2（R）的范數(shù)。可看出噪聲在小波算子作用下，其模平方的平均值隨尺度s的增加而以的速度下降。因此，噪聲將隨著小波變換的尺度的增大而得到很好的壓制。

利用有用信號和噪聲小波變換的極大模隨小波變換尺度的變化的規(guī)律，不僅可以區(qū)別有用信號和噪聲，還可以有效地壓制噪聲。小波復信號分析就是將小波分析引入到復信號分析中，能更好地對信號進行有效的多參量分析，從多個角度分析雷達剖面使得解譯更準確。

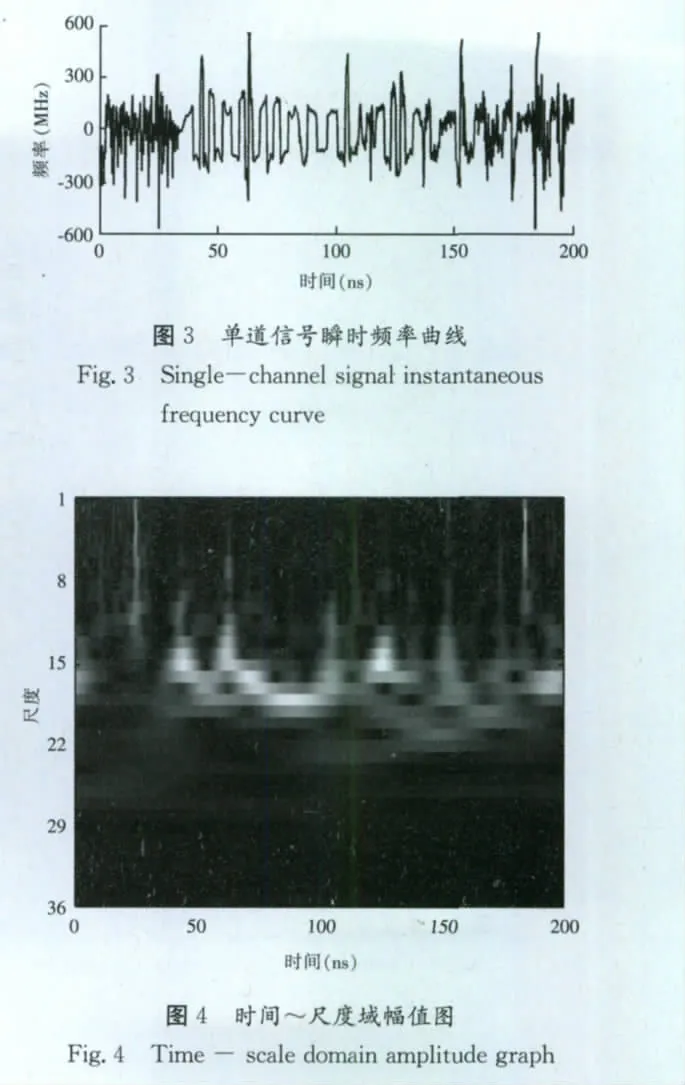
圖3展示的是對一探測數(shù)據(jù)進行瞬時頻率分析，不但受到了高頻的噪聲干擾，還存在一定的尖峰脈沖。對其進行連續(xù)小波正變換，其時間～尺度域幅值圖如圖4所示，重構(gòu)尺度11～32，得到處理后的瞬時頻率曲線如圖5所示（見下頁），可看出噪聲和尖峰得到很好的壓制。因此對復信號分析的剖面做小波處理能大大增強其可視效果。

1.4 連續(xù)小波變換及反變換的程序?qū)崿F(xiàn)

式（13）給出了連續(xù)小波變換（CWT）定義：

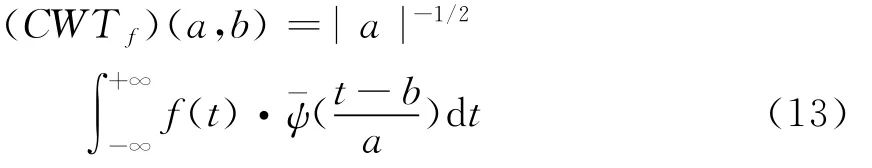
連續(xù)小波變換重構(gòu)公式為：

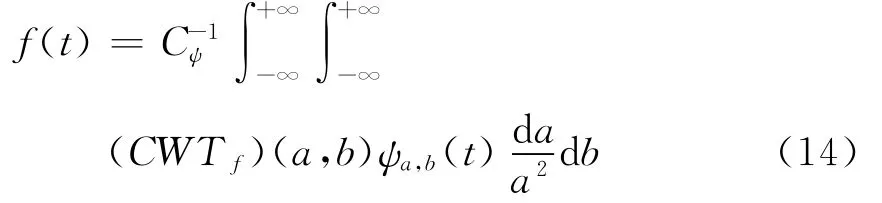
a≠0，a、b∈R。由函數(shù)ψ（t）經(jīng)過尺度伸縮和平移得到。

待處理的信號進入計算機前須離散化，連續(xù)小波變換在計算機上程序?qū)崿F(xiàn)過程為：

（1）首先對離散信號xn做離散傅里葉變換，如式（15）所示。

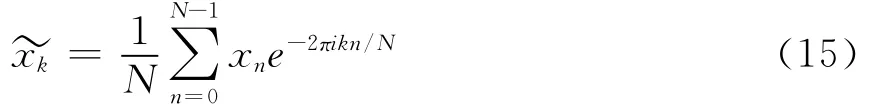
（2）再對小波基進行傅氏變換后就得到信號xn連續(xù)小波變換，如式（16）所示。

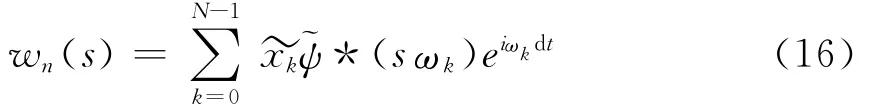
其中 s為尺度；dt為采樣間隔，ωk如式（17）。

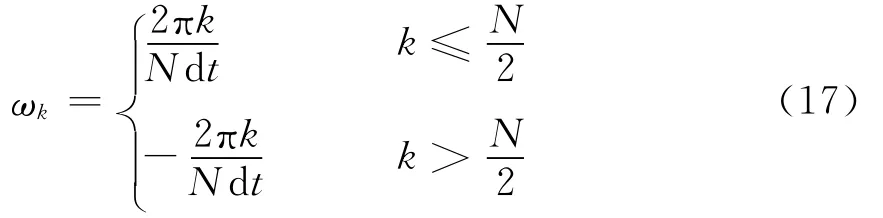
（3）最后進行連續(xù)小波變換重構(gòu)，其重構(gòu)公式為：

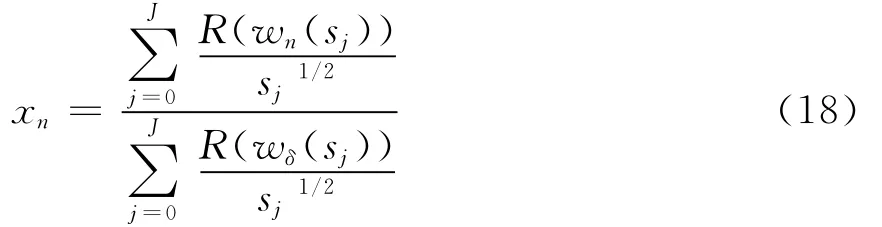
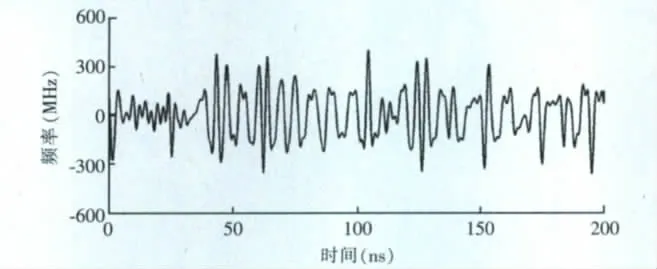
圖5 單道信號小波瞬時頻率曲線Fig.5 Single－channel signal wavelet instantaneous frequency curve

2 實測數(shù)據(jù)的小波復信號處理

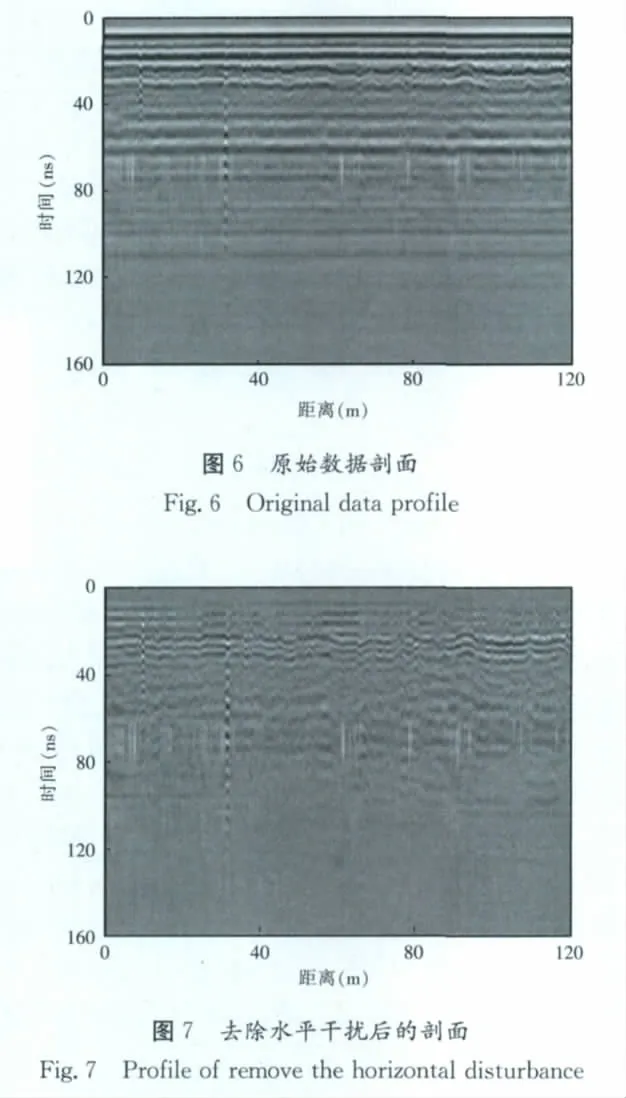
下面是一段鐵路實測數(shù)據(jù)，由于噪聲的干擾且深部反射信號微弱，深部異常體難以識別。

其原始數(shù)據(jù)剖面和去除水平干擾后的剖面分別如圖6、圖7所示。

對去水平干擾后的原始數(shù)據(jù)進行復信號分析得到多參數(shù)剖面，如圖8所示（見下頁）。可以明顯看出，雖然復信號分析剖面中瞬時相位剖面比原始數(shù)據(jù)剖面對深部弱信號具有更好的反映，但復信號分析受到嚴重的噪聲干擾。

經(jīng)小波復信號分析，得到小波復信號分析剖面，如圖9所示（見下頁）。可以看出，復信號分析中的噪聲得到了很好的壓制，剖面更加清晰，尤其是小波瞬時相位、小波瞬時頻率能更好地提取深部介質(zhì)弱反射信號。

在原始數(shù)據(jù)中，很難辨認繞射弧，在小波瞬時相位、小波瞬時頻率剖面圖中得以清晰的展現(xiàn)。小波瞬時振幅剖面也能較好地展示道床的起伏形態(tài)。因此采用小波復分析提取深部的弱信號的方法切實可行。

3 結(jié)論

在當前技術(shù)條件下，地質(zhì)雷達的發(fā)射功率有限，因而接收的深部反射信號甚是微弱，其應(yīng)用的勘探深度受到限制，弱信號的提取問題一直備受關(guān)注。小波復信號分析綜合了復信號分析對弱信號的提取能力和連續(xù)小波變換對噪聲的壓制能力，能更好地對弱信號進行識別，提高地質(zhì)雷達的勘探能力和勘探效果。

［1］ 李大心.探地雷達方法與應(yīng)用［M］.北京：地質(zhì)出版社，1994.

［2］ 柳剛，李術(shù)才，薛翊國，等.基于小波變換的雷達低信噪比信號處理技術(shù)及應(yīng)用研究［J］.工程勘察，2009（9）：85.

［3］ 詹毅，梁昌洪，方廣有.探地雷達回波信號處理中小波變換域濾波方法的研究［J］.西安電子科技大學學報，1999，26（3）：305.

［4］ 師學明，張劍，劉夢花，等.小波變換在地質(zhì)雷達干擾波壓制中的應(yīng)用［J］.工程地球物理學報，2008，5（3）：279.

［5］ 許建文，汪堅，吳江寧，等.小波分析在地質(zhì)雷達數(shù)據(jù)去噪中的運用［J］.重慶交通學院學報，2007，26（1）：108.

［6］ 張英德，劉江平，劉良瓊.Hilbert變換在地質(zhì)雷達數(shù)據(jù)處理中的應(yīng)用［J］.工程地球物理學報，2004，1（4）：349.

［7］ 湯井田，化希瑞，曹哲民，等.Hilbert－Huang變換與大地電磁噪聲壓制［J］.地球物理學報，2008，51（2）：603.

［8］ 皮紅梅，劉財，王典.利用 Hilbert—Huang變換提取地震信號瞬時參數(shù)［J］.石油地球物理勘探，2007，42（4）：418.

［9］ 黃海，陳祥獻.Hilbert—Huang變換應(yīng)用中的預處理方法研究［J］.浙江大學學報，2007，41（3）：431.

［10］韋宏鵠，楊順安.探地雷達波的相位參數(shù)及其應(yīng)用［J］.地質(zhì)科技情報，1999，18（1）：102.

［11］肖兵，鮑光淑，趙秋梅，等.探地雷達復信號分析及改進［J］.中南工業(yè)大學學報，1997，28（1）：1.

［12］張恩厚，陳前新.瞬時振幅、瞬時相位、瞬時頻率在地質(zhì)雷達工程中的應(yīng)用［J］.安徽地質(zhì)，2004，14（1）：58.

［13］謝雄耀，萬明浩.復信號分析技術(shù)在地質(zhì)雷達信號處理中的應(yīng)用［J］.物探化探計算技術(shù)，2000，22（2）：108.

［14］張志勇，胡敬濃，張麗嬌，等.探地雷達復信號分析的幾點討論［J］.物探化探計算技術(shù)，2006，28（2）：146.

［15］ MALLAT S，HWANG W L.Singularity detection and processing with wavelets［J］.IEEE Trans Inform Theory，1992，38：617.

［16］楊新安.地質(zhì)雷達檢測鐵路路基新技術(shù)［J］.中國鐵路，2004：41.

［17］DAVIS JL，ANNAN AP.Ground penetrating radar for high resolution mapping of soil and rock stratigraphy［J］.Geophys Prospect，1989，37：531.

［18］MASER KR.Condition assessment of transportation infrastructure using ground penetrating radar［J］.J Infrastruct Syst，1996（2）：94.

［19］廖立堅，楊新安，杜攀峰.鐵路路基雷達探測數(shù)據(jù)的處理［J］.中國鐵道科學，2008，29（3）：18.

［20］楊峰，彭蘇萍，張全升，等.地質(zhì)雷達精細處理技術(shù)方法的應(yīng)用研究［J］.工程勘察，2007（4）：70.

［21］黃吉林，黃忠來，張建中，等.探地雷達小目標信號時頻特征分析［J］.廈門大學學報，2011，50（1）：17.

［22］JACK R，JACKSON P.Imaging attributes of railway track formation and ballast using ground probing radar［J］.NDT＆E International，32－1999：457.

［23］華劍飛.物探技術(shù)在路基病害檢測中的應(yīng)用［J］.鐵道標準設(shè)計，2002（7）：56.

［24］DANIELS DJ.Surface Penetrating Radar electronics Communication Engineering Journal［J］.IEEE，1996，8（4）：121.

P 631.4

A

10.3969／j.issn.1001－1749.2012.05.17

1001—1749（2012）05—0593—06

2011－12－19 改回日期：2012－04－18

黃敏（1985－），男，回族，湖南常德人，碩士，主要從事電磁法勘探工作。