一個特定型函數極限的計算與推廣

曲元海

(通化師范學院 數學系，吉林 通化 134002)

1 引言

解 顯然本題羅必達法則失效.故另謀方法.仔細觀察該題后，我們發現由于被積函數含有|cost|項(本題關鍵就在于此)，而該函數是周期為π的非負函數.另一方面，當連續變量x充分大時，總存在n∈，使x可表成x=nπ+x0，其中0≤x0<π，故有x→+∞?n→∞.

此時，本題可轉化為計算極限

由于

(1)

采用分部積分法，經計算獲得

……………………………………

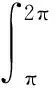
而對最后一項：

(1)當0≤x0<π/2時，令t=nπ+x，則有

(2)當π/2≤x0<π時，令t=nπ+x，則有

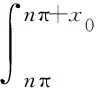
這時，將上述所有結果帶回(1)式，我們得到分子部分

故得

另解 由于被積函數含有|cost|是周期為π的非負函數.故當x充分大時，總存在自然數n∈，使nπ≤x≤(n+1)π.因此，由積分的單調性得

(2)

依照前邊定積分的計算方法得

(這里，對第二個積分取變量替換t=nπ+x).因此，當n→∞，必有

由(2)式及極限的兩邊夾定理，我們立即獲得相同結果.

注意：上述兩方法都離不開計算定積分，因此，兩方法本質上有密切聯系，只是求解角度不同.

3 推廣

以下我們只考慮應用夾逼定理來求解.由于當k≥4時，不僅導致計算積分值繁瑣，而且涉及高次冪的自然數求和.因此，本文我們僅限k=1，2，3時，推廣如下兩種對偶型積分的極限.

計算兩種特定的對偶型極限：

k=1，2，3.

事實上，當x充分大時，總存在自然數n∈，使nπ≤x≤(n+1)π，再由積分的單調性得

(3)

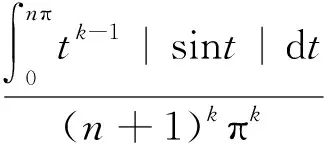
(4)

以下求解過程中，我們總是假設x→+∞時，存在n∈，使nπ≤x≤(n+1)π，不再特殊說明.

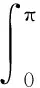
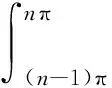
令k=1，代入(3)式，應用夾逼定理，立即獲得

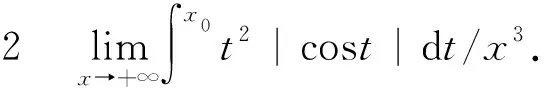
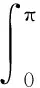
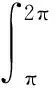
故

令k=3，代入(3)式，由夾逼定理，立刻獲得

解 類似例1計算方法，更容易計算

令k=1，由(4)式及夾逼定理，顯然獲得

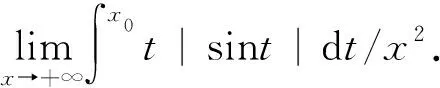
解 利用不定積分

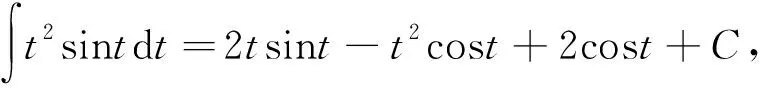
故

因此，必有

令k=3，代入(4)式，應用夾逼定理，我們獲得

綜上所述，獲得本文如下的推廣結論

最后，我們給出一個猜想，?k∈，是否

參考文獻：

[1]劉玉璉，傅沛仁.數學分析講義[M].第三版.北京:高教出版社，1997.

[2]陳紀修，於崇華，金路.數學分析[M].北京;高等教育出版社，1999.

[3]劉三陽，于力，李廣民.數學分析選講[M].北京;科學出版社，2007.