P-內射的WB-環
李艷午,儲茂權,程海霞,3
(1.蕪湖信息技術職業學院,安徽蕪湖 241000;2.安徽師范大學數學與計算機科學學院,安徽蕪湖 241000; 3.南京大學數學系,江蘇南京 210093)
0 引言
設R是環,M為右R-模,如果每個主右理想aR到M的右R-同態能夠擴張成RR到M的同態,那么,稱模M為右P-內射模;如果RR是右P-內射模,則稱環R為右P-內射環[1].內射性是關于環的一個很重要的性質,許多研究人員都對其做了深入而廣泛的研究,取得了許多結果[1,2].
環R稱為正則環,是指對任意的a∈R,存在,b∈R,使得,a=aba.正則環的研究一直吸引著研究人員的興趣,并取得了一些結果[3].近年來,又有研究人員研究了正則環上的模比較結構,例如,陳煥垠[4]研究了正則的WB-環,得到了這種環上的部分比較結構.受此啟發,本文研究了P-內射的WB-環,推廣了文獻[4]的部分結果,同時也使文獻[1,2]的部分結果得到拓展和延伸.
1 預備知識
本文中的環R都是有單位元的結合環,稱環R的理想I,J是正交的.如果,IJ=JI=0,設M和N為右R-模,M<⊕N表示M同構于N的子模.設I是環R的理想,稱a∈R是模I右(左)可逆,如果存在u∈R,使得,

2 主要結果及證明
定理1 設R是非奇異的P-內射環,并且滿足特殊左零化子的升鏈條件,則下列條件等價:
(1)R是WB-環;
(2)對任何a∈R,有正交理想I,J,使得,a=aua =ava,這里u∈R模I右可逆,v∈R模J左可逆.
證明 (1)?(2).
由于R是非奇異的P-內射環,所以存在一個環R的理想L,且L≠0,使得,l(a)⊕L是R的本質左理想[5].令b∈L,且b≠0.如果r1,r2∈R,且使得,r1ba=r2ba,那么,(r1b-r2b)a=0,r1b-r2b∈l(a)∩L,考慮到,l(a)∩L=0,由此可推出,r1b=r2b.于是,我們可以定義,f:Rba→R,rba|→rb.易見,f是左R-同態.又因為R是P-內射的,從而存在x∈R,使得,rb=f(rba)=rbax1,對所有r∈R.特別地,對r=1,可得到,b=bax1,等式兩邊右乘a,又得到,b(a-ax1a)=0,b∈l(a-ax1a).再由,0≠b∈L和l(a)∩L=0,可推出b?l(a).因此有,l(a)?≠l(a1),這里,a1=a-ax1a.
重復上面的步驟,我們可以假定:

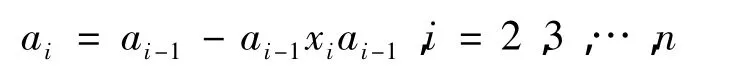
由于R滿足特殊左零化子的升鏈條件,于是可以假定,l(an)=l(an+1).如果,l(an)=l(an+1)≠R,那么,an≠0.于是由上面的過程可推出,l(an)?≠l(an+1),此與l(an)=l(an+1)矛盾.因此,我們得到,l(an)=l(an+1)=R,an=0,故,an-1= an-1xnan-1,an-1=an-2-an-2xn-1an-2.由文獻[3]可知,an-1是正則的.類似地進行下去,最后得到,a= axa,對某個x∈R,即環R是正則環.于是對,a∈R,存在x∈R,使得,a=axa,x=xax,而ax+(1-ax) =1,故根據文獻[4]有正交理想I,J和y,z∈R,使得,u=x+y(1-ax)∈R模I右可逆,v=x+z(1 -ax)∈R模J左可逆.容易驗證,a=axa=aua= ava.
(2)?(1).

由于Goldie環是滿足特殊左零化子升鏈條件的[6],所以有:
推論1 設R是非奇異的P-內射環,如果R又是Goldie環,那么下列等價:
(1)R是WB-環;
(2)對任何a∈R,有正交理想I,J,使得,a= aua=ava,這里,u∈R模I右可逆,v∈R模J左可逆.
根據文獻[7]的定理2,半素的P-內射環是非奇異的,所以結合定理1有:
推論2 設R是半素的P-內射環,如果R滿足特殊左零化子的升鏈條件,那么下列等價:
(1)R是WB-環;
(2)對任何a∈R,有正交理想I,J,使得,a= aua=ava,這里,u∈R模I右可逆,v∈R模J左可逆.
定理2 設R是非奇異的P-內射環,如果R不包含由有限非零主左理想構成的直和項,那么下列等價:
(1)R是WB-環;
(2)對任何a∈R,有正交理想I,J和冪等元e∈R,使得,a=eu=ev,這里,u∈R模I右可逆,v∈R模J左可逆.
證明 (1)?(2).
令a∈R并且a≠0.由假設,存在x1∈R,x1≠0,使得,l(a)⊕Rx1?l(a1),這里,a1=a-ax1a.如果,l(a1)=R,那么,a1=0,即,a=ax1a.若l(a1)≠R,則a1≠0.類似地,存在b2∈R,b2≠0,使得,l(a1)⊕Rb2?l(a2),a2=a1-a1x2a1.由此,得到,l(a)⊕Rb1⊕Rb2?l(a2),a1=a-ax1a,a2=a1-a1x2a1.
由于R不包含由有限個非零主左理想構成的直和項,那么重復上面的步驟,我們可以假定:

由l(an)=R,可推出an=0,因此,

最后,根據文獻[5],存在x∈R,使得,a=axa,即證明了環R是正則環.于是,對a∈R,存在x∈R,使得,a=axa和x=xax,又因為,ax+(1-ax)= 1,所以,u=a+(1-ax)y∈R模I右可逆,v=a+ (1-ax)z∈R模J左可逆.令e=ax,則e2=e∈R,且,a=eu=ev.
(2)?(1).
令a∈R,由于R是正則環,從而存在x∈R,使得,a=axa和x=xax.由假設,存在正交理想I,J和冪等元e=R,使得,x=eu=ev,這里,u∈R模I右可逆,v∈R模J左可逆.注意到,xa+(1-xa)=1,于是,eua+(1-xa)=1,從而,e+(1-xa)(1-e) =1-eua(1-e)∈R可逆,那么,x+(1-xa)(1-e)u=(1-eua(1-e))u,令u′=(1-eux(1-e))u,則,a=axa=au′a,這里,u′∈R模I右可逆.同理,存在v′∈R,使得,v′∈R模J左可逆.最后,由定理1得證R是WB-環.
稱x,y∈R為相對于a是可交換的,如果axy= ayx,一個環R稱為CF環,如果R的每個補左理想是有限生成的并且生成子的右單位元素相對于那個生成子是可交換的[4],稱,a,b∈R為相似.如果有可逆元u∈R,使得,a=ubu-1,記為a~b;稱a,b∈R為偽相似.如果有x,y,?z∈R,使得,xay=b,zbx= a,xyx=xzx=x,記為ab.下面就用偽相似來刻畫P-內射WB-環.
定理3 設R是非奇異的P-內射環,如果R又是CF環,那么下列等價:
(1)R是W?B-環;
(2)如果ab,a,b∈R,則有正交理想I,J,使得,au=ub,av=vb,其中,u∈R模I右可逆,v∈R模J左可逆;
(3)如果eR?fR,e,f∈R為冪等元,則有正交理想I,J,使得,
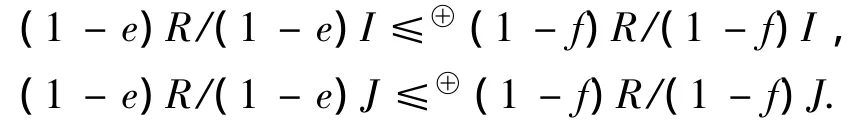
證明 根據文獻[2]的定理5,由假設可知環R是正則的,再根據文獻[4]的定理3.1得,(1)與(2)和(3)的等價性.
推論3 設R是非奇異的P-內射環,如果R又是CF環,那么下列等價:
(1)R是WB-環;
(2)如果aR?bR,a,b∈R,則有正交理想I,J,使得,
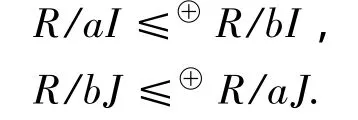
證明 (1)?(2).
由條件以及文獻[2]的定理5知,環R是正則環.如果,aR?bR,a,b∈R,那么存在冪等元e,f∈R,使得,aR=eR,bR=fR,從而,eR?fR.于是,由定理3知,存在正交理想I,J,使得,

不難證明,

同理,
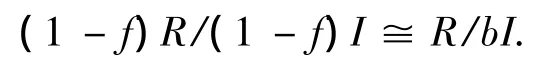
故,

(2)?(1).
假定eR?fR,e,f∈R為冪等元,則有正交理想I,J,使得,

又易見,

同理,

最后,根據定理3知R是WB-環.
定理4 設R是非奇異的P-內射環,且滿足特殊左零化子的升鏈條件,則下列條件等價:
(1)R是WB-環;
(2)如果aR?bR,a,b∈R為冪等元,則有正交理想I,J,使得,au=ub,av=vb,這里,u∈R模I右可逆,v∈R模J左可逆.
證明 (1)?(2).
如果aR?bR,a,b∈R為冪等元,則有,r1∈?aRb,r2∈bRa,使得,a=r1r2,b=r2r1,由此可得,a
b.故由定理3得證.
(2)?(1),是定理3的直接結果.
稱a∈R有Drazin逆,如果存在,n∈N,r∈R,使得,an=an+1x,ax=xa,xax=x,稱x為a的Drazin逆,記為ad.
定理5 設R是非奇異的P-內射環,則R只要再滿足下列條件之一:
(a)特殊左零化子的升鏈條件;
(b)R是CF環;
(c)R是Goldie環;
(d)R不包含由有限非零主左理想構成的直和項.
就有,
(1)R是WB-環;
(2)如果ab,ba,a,b∈R有Drazin逆,則有正交理想I,J,使得,
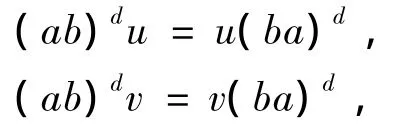
這里,u∈R模I右可逆,v∈R模J左可逆,等價.
證明 (1)?(2).
首先,易知R只要再滿足上述條件之一,那么R就是正則環.如果ab,ba,a,b∈R有Drazin逆,則存在,n∈N,使得,
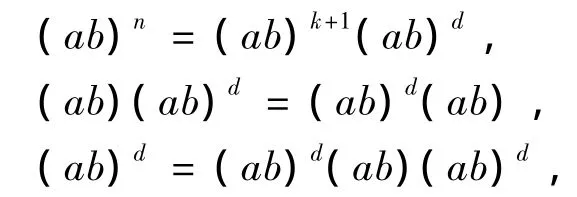
從而就有,

于是,
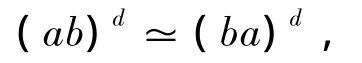
最后,由定理3可證.
(2)?(1).
如果aR?bR,a,b∈R為冪等元,則有,r1∈aRb,r2∈bRa,使得,a=r1r2,b=r2r1.顯然,a,b都有Drazin逆,于是有正交理想I,J,使得,
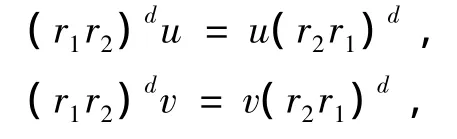
其中,u∈R模I右可逆,v∈R模J左可逆.由定理4得R是WB-環.
[1]Nicholson W K.Principally Injective Rings[J].Journal of Algebra,1995,174(1):77-93.
[2]Zhang J L.P-injective Rings and Von-Neumann Regular Rings[J].Northeast Math J,1991,7(3):326-331.
[3]Goodearl K R.Von Neumann Regular Rings[M].London: Pitman,1979.
[4]陳煥垠.正則的WB-環[J].數學學報,2006,49(6): 1311-1320.
[5]Faith C,Algebra II:Rings Theory[M].New York:Springer-Verlag,1976.
[6]Chattes A W,Hajarnavis C R.Rings with Chain Conditions[M].London:Pitman,1980.
[7]Zhang J L.On Nonsingular Rings[J].Journal of Anhui Normal University(Natural Science),1986,9(4):6-11.

