基于平行算法的非擴張映像的最小范數不動點

劉 霞, 李曉焱,2, 李曉娜

(1.榆林學院數學系,陜西榆林719000;2.西安建筑科技大學數學系,陜西西安710055)

1 引言和預備知識

設C是實Hilbert空間H的非空閉凸子集,T:C→H是非擴張映像,則對于?x,y∈C,‖Tx-Ty‖≤‖x-y‖.F(T)={x∈C:x=Tx}為T的不動點集.度量(最近點)投影映射PC:H→C指:對?x∈H,PCx是C中的唯一的點,且‖x-PCx‖=inf{‖x-y‖:y∈C}.如果 F(T)≠φ,可以證明 F(T)是 Hilbert空間中非空閉凸子集,于是存在唯一的x?∈F(T)滿足‖x?‖=min{‖x‖:x∈F(T)},則稱 x?是T的最小范數不動點,從而 x?是從原點到F(T)的最近點投影,即x?=PF(T)(0).記:xn→x表示{xn}強收斂于 x;xn?x表示{xn}弱收斂于 x;w={x:?xnj?x}為{xn}的弱極限集.

文獻[1]對Halpern[2]方法做了改進,當0?C,修改后的迭代序列xn依然收斂于C中一個不動點.在此基礎上,結合文獻[3-10],利用平行算法和最近點投影算子對有限多非擴張映像的最小范數不動點做進一步地研究.

性質1[1,6,11]投影映射的基本性質

(i)＜x-PCx,y-PCx＞≤0,?x∈H,?y∈C;

(ii)＜x-y,PCx-PCy＞≥‖PCx-PCy‖2,?x,y∈H;

(iii)‖x-PCx‖2≤‖x-y‖2-‖y-PCx‖2,?x∈H,?y∈C.

引理1[1,5]半閉原理,設C是實Hilbert空間H的非空閉凸子集,T:C→C是非擴張映射,當 n→∞時,如果 xn?p,且‖xn-Txn‖→0,則 p是T的不動點,即 p∈F(T).引理2[1,6,12]設{αn}是一個滿足下列條件的非負實數序列

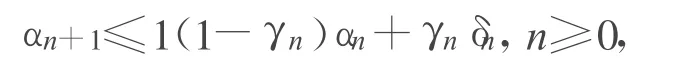
2 主要結果

引理3 設C是實Hilbert空間H的非空閉凸子集,{T1,…,Tn}是C上的N個非擴張自映射,對于所有的1≤i≤N,λi＞0,且,那么算子是非擴張的 .

證明 對任意的 x,y∈C,有

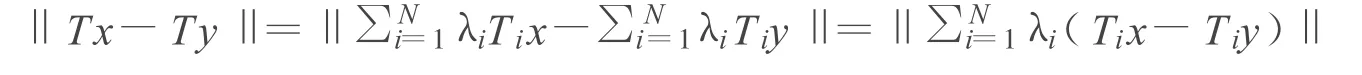
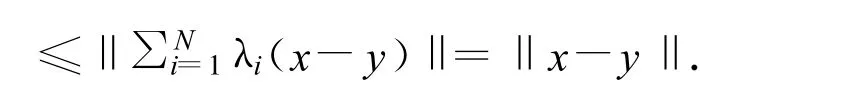
定理 設 C是實Hilbert空間 H的非空閉凸子集,{T1,…,TN}是 C上的N個非擴張自映射,且φ≠F(T):=∩Ni=1F(Ti)=(T1T2…tN),假定{tn}滿足下列條件:

(B1)

任取初始值x0∈C,序列{xn}通過平行算法定義為則序列{xn}強收斂于非擴張映像的公共最小范數不動點.

證明 (1)證明{xn}有界.任取 p∈F(T)由式(1)可推得

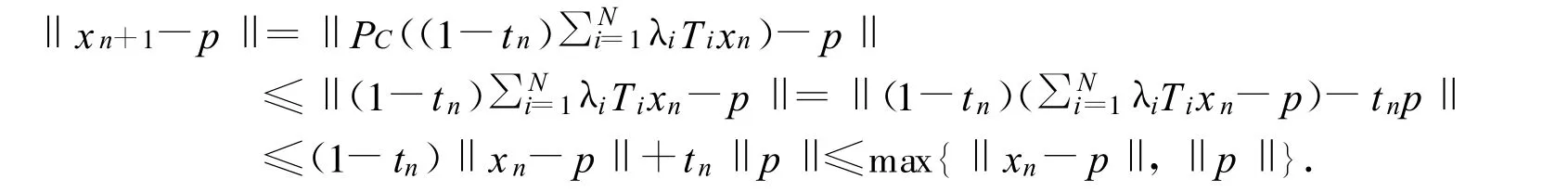
所以,對所有的 n≥0歸納可得:‖xn-p‖≤max{‖x0-p‖,‖p‖}.于是序列{xn}有界,即存在 M＞0,使對所有的 n,恒有 M≥max{‖xn‖,‖Txn‖}成立.

(2)證明‖xn+1-xn‖→0.利用 PC的非擴張性和式(1)得

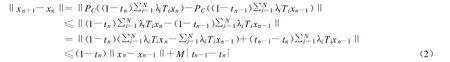
由引理2,條件(B3)和式(2)可得‖xn+1-xn‖→0.

(3)證明 ωn(xn)?F(T).

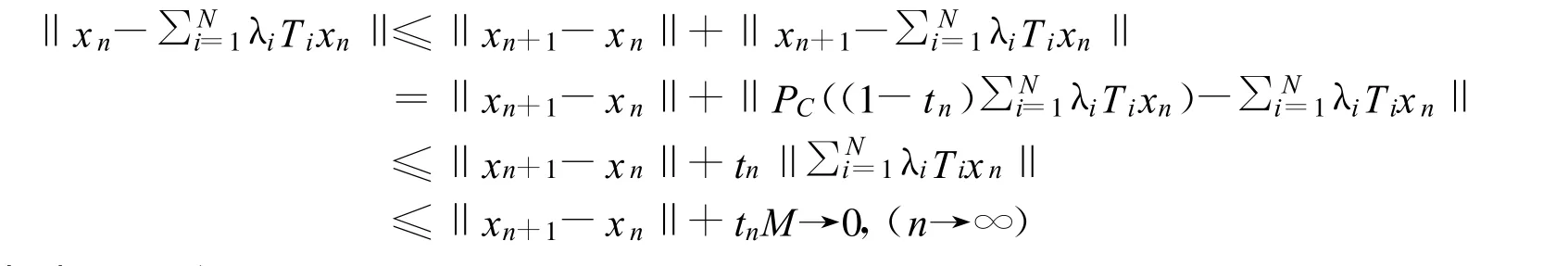
由引理1可得 ωn(xn)?F(T).

因為{xn}有界,所以不失一般性可設 xn′?x′∈F(T).又 x?=PF(T)(0),所以由性質 1(i)和(3)式可得

(5)最后證明xn→x?

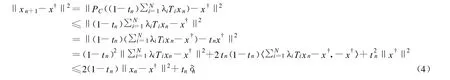
其中

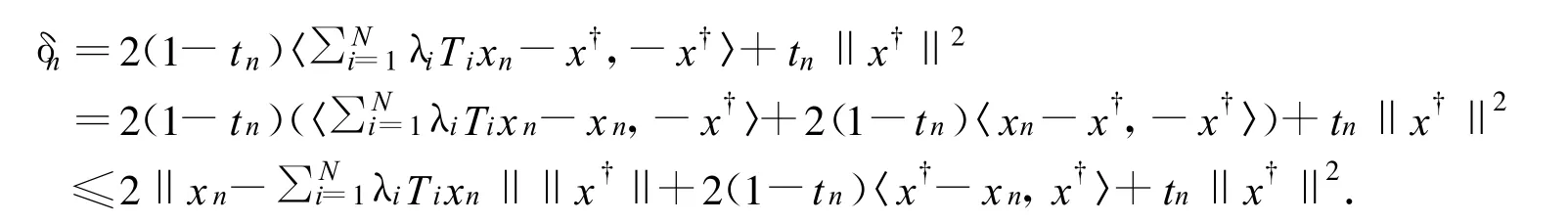
如果上述定理只有一個映射,即i=1,則有下述推論成立.

推論 設C是Hilbert空間H的非空閉凸子集,T:C→C非擴張映像,F(T)≠φ,x0∈C.設{tn}∈(0,1),并滿足上述定理中的(B1),(B2),(B3)條件.序列{xn}定義為

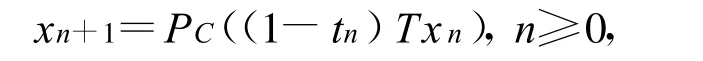
則

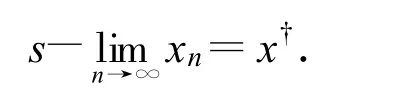
致謝:感謝榆林學院科研啟動項目(11gk64)對本文的資助

[1] Y L Cuiand,X Liu.Noteson Browder's and Halpern's methods for nonexpansive mappings[J].Fixed Point Theory,2009,10(1):89-98.

[2] B Halpern.Fixed points of nonexpanding maps[J].Bull.Amer.Math.Soc.,1967,73:957-961.

[3] S Reich.Approximating fixed points of nonexpansive mappings[J].Panamerican.Math.J.1994,4(2):23-28.

[4] H K Xu.Iterative algorithms for nonlinear operators[J].J.London Math.Soc.,2002,66:240-256.

[5] H K Xu.Remarks on an iterative method for nonexpansive mappings[J].Comm.Appl.Nonlinear Anal.2003,10(1):67-75.

[6] Y H Yao,R D Chen,H K Xu.Schemes for finding minimum-norm solutions of variational inequalities[J].Nonlinear Analysis,2010,72:3447-3456.

[7] F E Browder.Convergence theorems for sequences of nonlinear operators in Banach spaces[J].Math.Z.,1967,100:201-225.

[8] Z Opial.Weak convergence of the sequence of successive approximations of nonexpansive Bull.Amer.Math.Soc.mappings,1967,73:595-597.

[9] R.Wittmann,Approximation of fixed points of nonexpansive mappings[J].Arch.Math.1992,58:486-491.

[10] D P Wu.Weak Convergence of Ishikawa Iteration with Error for Pseudo Contractive Mappings in Hilbert Spaces[J].Journal of Mathematics Research,2011,3(4):44-49.

[11] K Geobeland,W A Kirk.Topicsin Metric Fixed Point Theory[M].Cambridge Studiesin Advanced Mathematics.Cambridge University Press,1990.

[12] H K Xu.Strong convergence of an iterative method for nonexpansive and accretive operators[J].J.Math.Anal.Appl.2006,314:631-643.