若干圖的鄰點可區別的I-全染色和鄰點可區別的I-均勻全染色

張 婷， 趙慧霞， 杜 佳， 趙雙柱

(蘭州文理學院 a.教育學院, b.學報編輯部, c.數字媒體學院, 甘肅 蘭州 730000)

0 引 言

圖的染色起源于地圖著色問題，它是圖論中的一個重要分支，其基本問題之一就是確定各種染色法的色數. 圖G的I-全染色是指對圖G的頂點和邊進行染色,使得任意兩個相鄰頂點的顏色不同,任意兩條相鄰邊的顏色不同. 圖G的一個鄰點可區別的I-全染色是指:在圖G的I-全染色的基礎上，還滿足任意兩個相鄰頂點的色集合不同,即C(u)≠C(v),其中,C(u)={f(u)|u∈V(G)}∪{f(uv)|uv∈E(G),v∈V(G)}.而圖的鄰點可區別的I-全染色中所用顏色的最少數量稱為圖G的鄰點可區別I-全色數. Zhang等[1]于2009年提出了圖的鄰點可區別I-全染色概念, 拓展了圖染色理論的應用領域. 之后, 一些學者對一些特殊圖的鄰點可區別I-全染色和點可區別I-全染色進行了研究[2 - 6]. 文獻[2]研究了Pm∨Sn,Sm∨Fn,Sm∨Sn和Sm∨Wn的鄰點可區別I-全染色，得到了它們的鄰點可區別I-全色數; 文獻[3]給出了路、扇和星的Mycielski圖的鄰點可區別I-全色數,文獻[4]研究并給出了若干倍圖鄰點可區別I-全色數.

圖的均勻染色強調了任意兩個色類的顏色個數最大相差為1,它常用來解決一些分配、調度及負載平衡問題. 均勻染色的概念最早是由Meyer[7]于1973年提出的,這個概念的提出揭開了圖的均勻染色的序幕, Fu[8]于1994年提出了均勻全染色概念及均勻全染色猜想, 1996年，Zhang[9]獨立地提出了圖的均勻全色數概念.他們在研究了一些簡單圖的均勻全色數之后，提出了均勻全染色猜想:任意簡單圖的均勻全色數至多為最大度加2,自此揭開了圖的均勻全染色研究的序幕. 2015年，王繼順[10]得到了路、圈、扇、輪、完全圖和完全二部圖的鄰點可區別I-均勻全色數，并提出鄰點可區別I-均勻全色數最大不超過Δ(G)+2的猜想. 之后，許多學者圍繞圖的均勻全染色問題做了大量研究[11 - 13].文獻[14]研究了若干Mycielski圖的鄰點可區別的I-均勻全染色, 文獻[15]研究了幾類特殊圖的鄰點可區別I-均勻全染色. 本文根據路、圈、星、扇和輪的平方圖的構造特征,研究并確立了它們鄰點可區別I-均勻全色數,驗證了它們的色數滿足猜想給出了圖C5∨Wn的鄰點可區別的I-全染色,進一步補充了文獻[2].

定義1[10]若連通圖G(V,E)的階|V(G)|≥2,f是從V(G)∪E(G)到{1,2,…,k}的映射，k是自然數，若f滿足以下三點：

(1)對?uv∈E(G),u≠v,有f(u)≠f(v);

(2)對?uv,uw∈E(G),v≠w,f(uv)≠f(uw);

(3)對?uv∈E(G),u≠v,C(u)≠C(v),

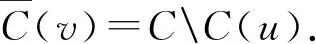
定義2[10]若連通圖G(V,E)的階|V(G)|≥2且f是G(V,E)的一個k-I-AVDTC，若f滿足?i,j∈{1,2,…k},i≠j,有||Ti|-|Tj||≤1，則稱f為G的一個k-鄰點可區別I-均勻全染色(簡記為k-I-AVDETC),稱=min{k|存在G的k-I-AVDETC}為G的鄰點可區別I-均勻全色數，其中，Ti=Vi∪Ei,Vi={v|v∈V(G),f(v)=i},Ei={e|e∈E(G),f(e)=i}.

定義3[10]對于一個簡單圖G，V(Gk)=V(G),E(Gk)=E(G)∪{uv|d(uv)≤k}，其中，d(uv)是u和v的距離.當k=2時,稱此圖為G的平方圖.

定義4[2]兩個不相交圖的聯圖就是把一個圖G(V1,E1)的每個頂點與另一個圖H(V2,E2)的每個頂點連接起來所得到的圖，記作G(V1,E1)∨H(V2,E2), 其中，

V=V1∪V2,E=E1∪E2∪{uv|u∈V1,v∈V2}.

引理1[10]若連通圖G的階|V(G)|≥2,則有表示G的最大度.

引理2[10]若連通圖G的階|V(G)|≥2,且G有相鄰的最大度點,則有

引理3[10]設Kn為n(n≥3)階完全圖，則

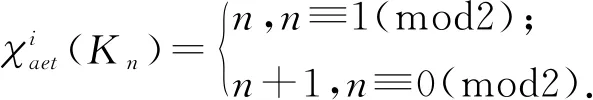
猜想1[10]對簡單連通圖G,有

文中未加說明的符號或術語參見文獻[16].

1 路、圈、星、扇和輪的平方圖的鄰點可區別I-均勻全色數

本部分根據路、圈、星、扇和輪的平方圖的構造特征,研究并確立了它們鄰點可區別I-均勻全色數.

定理1設Pn為n(n≥3)階的路，則有

證明以下分四種情形證明本定理.

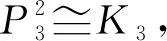
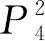
為驗證上述染色法f是鄰點可區別的，現列出各頂點的色集合：

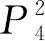
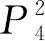
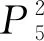
為驗證上述染色法f是鄰點可區別的，現列出各頂點的色集合:

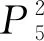
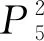
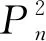
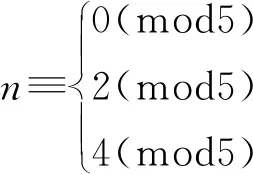
令f為點v1,v2,…,vn用1,2,3,4,0循環著色；邊v1v2,v2v3,…,vn-1vn用0,1,2,3,4循環著色；邊v1v3,v2v4,…,vn-2vn用3,4,0,1,2循環著色.

為驗證上述染色法f是鄰點可區別的，現列出各頂點的色集合:

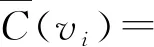
(i=2,3,…,n-2);

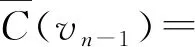
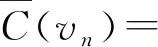
當n≡0(mod5)時，

當n≡2(mod5)時，

當n≡4(mod5)時，

從而此染色法是均勻的.

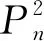
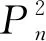
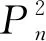
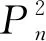
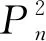
定理2對n階的圈Cn,當n≥4時,有

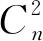
情形1當n≡0(mod5)時,令f為v1,v2,…,vn用1,2,3,4,0循環著色；v1v2,v2v3,…,vn-1vn,vnv1用3,4,0,1,2循環著色；v1v3,v2v4,…,vn-2vn,vn-1v1,vnv2用1,2,3,4,0循環著色.

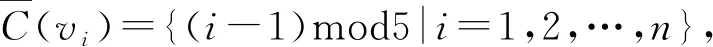
情形2當n≡1(mod5)時,令f為點v1,v2,…,v6用1,2,3循環著色；點v7,v8,…,vn用4,0,1,2,3循環著色；邊v1v2,v2v3,…,v6v7用4,0循環著色；邊v7v8,v8v9,…,vn-1vn,vnv1用1,2,3,4,0循環著色； 邊v1v3,v2v4,…,v5v7,v6v8用1,2,3循環著色； 邊v7v9,v8v10,…,vn-1v1,vnv2用4,0,1,2,3循環著色.

為驗證上述染色法f是鄰點可區別的，現列出各頂點的色集合:

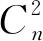
情形3當n≡2(mod5)時,令f為點v1,v2,…,v7用0,1,3,4,0,1,2著色；點v8,v9,…,vn用0,1,2,3,4循環著色；邊v1v2,v2v3,…,v7v8用4,0,1,2,1,2,3著色；邊v8v9,v9v10,…,vn-1vn,vnv1用4,0,1,2,3循環著色； 邊v1v3,v2v4,…,v7v9用2,3,3,4,4,0,1著色；邊v8v10,v9v11,…,vn-1v1,vnv2用2,3,4,0,1循環著色.

為驗證上述染色法f是鄰點可區別的，現列出各頂點的色集合:

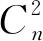
情形4當n≡3(mod5)時,令f為點v1,v2,…,v8用1,2,3,0,2,1,3,0著色；點v9,v10,…,vn用4,1,2,3,0循環著色；邊v1v2,v2v3,…,v8v9用4,0,4,1,4,3,4,2著色；邊v9v10,v10v11,…,vn-1vn,vnv1用1,2,3,4,0循環著色； 邊v1v3,v2v4,…,v8v10用1,2,3,0,2,1,0,3著色；邊v9v11,v10v12,…,vn-1v1,vnv2用4,0,1,2,3循環著色.

為驗證上述染色法f是鄰點可區別的，現列出各頂點的色集合:

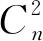
情形5當n≡4(mod5)時,令f為點v1,v2,…,v9用4,2,1,4,3,0,1,2,3著色,點v10,v11，…,vn用4,0,1,2,3循環著色,邊v1v2,v2v3，…,v9v10用1,2,3,2,3,4,0,4,0著色,邊v10v11,v11v12,…,vn-1vn,vnv,用1,2,3,4,0循環著色,邊v1v3,v2v4,…,v9v11用4,4,0,0,1,1,2,3,3著色, 邊v10v12,v11v13,…,vn-1v1,vnv2用4,0,1,2,3循環著色.

為驗證上述染色法f是鄰點可區別的，現列出各頂點的色集合:

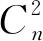
定理3對n+1階的星Sn,扇Fn,輪Wn,有

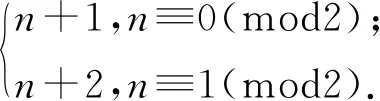
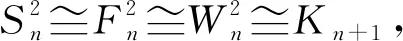
2 C5∨Wn的鄰點可區別I-全色數

本部分根據C5∨Wn的構造特征, 給出了C5∨Wn的鄰點可區別I-全色數.

定理4對m階的圈Cm和n+1階的輪Wn，當m=5時，有

情形1當n=3時，圖C5∨W3中有相鄰的最大度點,且Δ(C5∨W3)=8，由引理2知，為證定理為真,只需給出圖C5∨W3的一個9-I-AVDTC,為此構造映射f：V(C5∨W3)∪E(C5∨W3)→{1,2,…,9},令f為

f(ui)=i+3,i=1,2,…,5;f(v0)=9;

f(vj)=j,j=1,2,3;

f(uivj)=(i+j+3)9,i=1,2,…,5;j=0,1,2,3;

f(uiui+1)=i,i=1,2,3,4;

f(u5u1)=3;f(v0vj)=j,j=1,2,3;f(v1v2)=3;

f(v2v3)=5;f(v1v3)=4.

為驗證上述染色法f是鄰點可區別的，現列出各頂點的色集合：

可見,C5∨W3的9個頂點的色集合彼此互異,由定義,f是C5∨W3的一個5-I-AVDTC.

情形2當n≥4時,圖C5∨Wn只有一個最大度點,且Δ(C5∨Wn)=n+5,由引理1知,為證成立,只需給出圖C5∨Wn的一個n+5-I-AVDTC,為此構造映射f：V(C5∨Wn)∪E(C5∨Wn)→{1,2,…,n+5},以下分三種情況證明.

情形2.1當n=4時，令f為

f(ui)=n+i,i=1,2,3;

f(ui)=n+i-2,i=4,5;

f(v0)=n+5;f(vj)=j,j=1,2,…n;

f(uiv0)=n+i,i=1,2,…,5;

f(uivj)=i+j,i=1,2,…,5;

j=1,2,…,n-1;

f(v0vj)=j,j=1,2,…n;

f(uivn)=n+i+1,i=1,2,3;

f(u4vn)=2;f(u5vn)=5;

f(u1u2)=f(u3u4)=f(v2v3)=f(v1v4)=9;

f(u2u3)=f(u5u1)=f(v3v4)=1;

f(u4u5)=3;f(v1v2)=8.

為驗證上述染色法f是鄰點可區別的，現列出各頂點的色集合:

可見C5∨Wn, 當n=4時的10個頂點的色集合彼此互異,由定義,f是C5∨Wn(n=4)的一個n+5-I-AVDTC.

情形2.2當n=5時，令f為

f(ui)=n+i,i=1,2,3;

f(ui)=n+i-2,i=4,5;f(v0)=n+5;

f(vj)=j,j=1,2,…n;

f(uiv0)=n+i,i=1,2,…,5;

f(uivj)=i+j,i=1,2,…,5;j=1,2,…,n-1;

f(uivn)=n+i+2,i=1,2,3;

f(u4vn)=1;f(u5vn)=4;

f(u1u2)=10;f(uiui+1)=i-1,i=2,3,4;

f(u5u1)=1;f(v0vj)=j,j=1,2,…n;

f(vjvj+1)=n+2+j,j=1,2,3;

f(v4v5)=2;f(v5v1)=7.

為驗證上述染色法f是鄰點可區別的，現列出各頂點的色集合：

可見,C5∨Wn,當n=5時的11個頂點的色集合彼此互異,由定義,f是C5∨Wn(n=5)的一個n+5-I-AVDTC.

情形2.3當n>5時,令f為

f(ui)=n+i+1,i=1,2,3;

f(ui)=n+i-1,i=4,5;f(v0)=n+5;

f(vj)=j,j=1,2,…n-1;f(vn)=n+1;

f(uiv0)=n+i,i=1,2,…,5;

f(uivj)=i+j,i=1,2,…,5;j=1,2,…,n-1;

f(uivn)=(n+i+2)(n+5),i=1,2,…,5;

f(u1u2)=n+5；f(uiui+1)=i-1,i=2,3,4;

f(u5u1)=1;f(v0vj)=j,j=1,2,…n;

f(v1v2)=n+5；f(vjvj+1)=j-1,j=1,2,…n-1;

f(v1vn)=n+2.

為驗證上述染色法f是鄰點可區別的，現列出各頂點的色集合：

C(v1)={1,2,…,6,n+2,n+5};

C(v2)={1,2,…,7,n+5};

C(vj)={j-2,j-1,…,j+5},j=3,4,…,n-1;

C(vn)={1,2,n-2,n,…,n+5}.

可見,C5∨Wn,當n>5時的n+6個頂點的色集合彼此互異,由定義,f是C5∨Wn(n>5)的一個n+5-I-AVDTC.

綜上，定理得證.