基于整體最小二乘的穩健點云數據平面擬合*

官云蘭 劉紹堂 周世健 張立亭 魯鐵定

(1)東華理工大學測繪工程學院，撫州 344000 2)河南工程學院土木工程系，鄭州 451191 3)江西省科學院，南昌330029)

基于整體最小二乘的穩健點云數據平面擬合*

官云蘭1)劉紹堂2)周世健1，3)張立亭1)魯鐵定1)

(1)東華理工大學測繪工程學院，撫州 344000 2)河南工程學院土木工程系，鄭州 451191 3)江西省科學院，南昌330029)

針對點云數據平面擬合方法沒有完整考慮測量數據中的誤差及系數陣中誤差的情況，提出穩健整體最小二乘點云數據平面擬合方法。該法以整體最小二乘法為基礎，在考慮全部觀測量存在誤差的情況下，通過一定的準則刪除數據中的粗差或異常值，從而獲得穩健的平面參數估值。實驗中，分別利用最小二乘法、特征值法和穩健整體最小二乘擬合法對仿真點云數據和真實點云數據進行平面擬合，結果顯示該法能克服異常值的影響，得到可靠的平面參數估值，具有穩健性。

點云數據;整體最小二乘;平面擬合;異常值;穩健性

1 引言

地面三維激光掃描是一種新型的空間數據獲取技術，利用它可以對實物進行數字化，快速獲取物體表面大量點的三維坐標，稱為點云數據，從而迅速描繪和量化復雜環境。該技術為快速獲取空間數據提供了有效手段［1］。利用點云數據進行建模也成為許多3D建模研究人員關注的問題之一。

平面擬合是地面三維激光掃描數據處理中的常用步驟之一，通過平面擬合不僅可以實現平面標靶的定位，從而完成基于平面標靶的多視點云數據配準，也可以實現對真實場景中平面特征的建模。眾多學者［2-5］對從點云數據中提取平面特征進行了研究，包括最小二乘法、特征值法等。最小二乘法在假設x、y為獨立變量，不含誤差，而z為依賴變量，包含誤差的情況下解算平面參數，但由于點云數據獲取時x、y、z 3個方向均存在誤差，因此嚴格來說最小二乘法并不適合于點云數據平面擬合的解算;特征值法是在滿足條件a2+b2+c2=1情況下，根據平面方程ax+bY+cz=d計算平面參數，這種方法僅根據x、y、z 3個方向誤差的整體組合解算平面參數，并未單獨考慮各方向的誤差影響。文獻［5］在特征值算法的基礎上，以最小二乘法為原則，提出了穩健的平面擬合算法。本文則在考慮點云數據在x、y、z 3個方向上均有誤差、同時數據中存在粗差或異常值的情況下，提出基于整體最小二乘的穩健點云數據平面擬合算法。

2 整體最小二乘平面擬合

設空間平面方程為

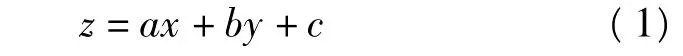
其中a、b、c為待估參數。

設對某一平面進行掃描，得到n個掃描點坐標{(xi，yi，zi)，i=1，2，…，n}。考慮到數據在x、y、z 3個方向均存在誤差，則方程改為：

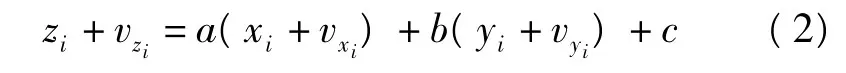
其中vx、vy、vz分別為x、y、z 3個方向的誤差改正數。

將上式整理，可得

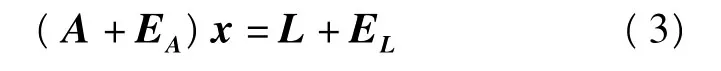
式中EA、EL分別表示矩陣A和向量L的誤差，即

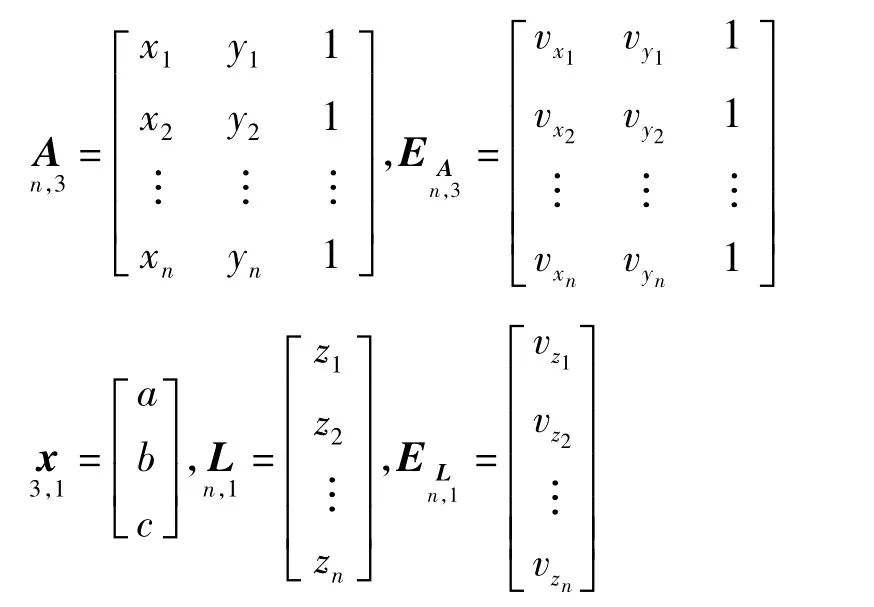
通常采用矩陣奇異值分解(SVD)解算待定參數的整體最小二乘解［6-8］。

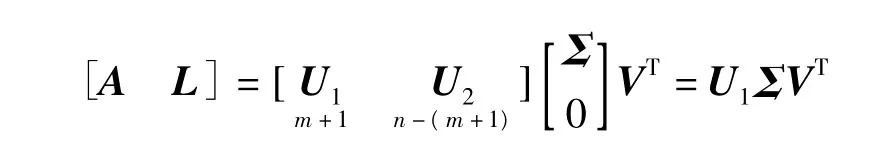
其中

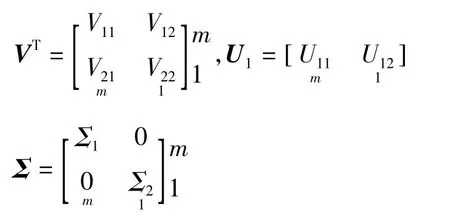
則參數的整體最小二乘估值為：

殘差矩陣為：

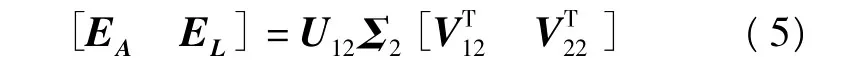
單位權中誤差為：

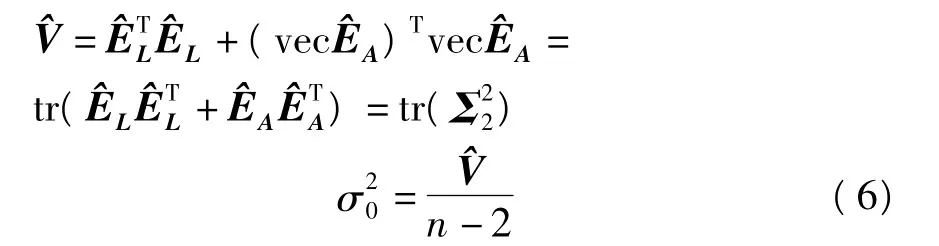
也可以采用如下公式進行計算［9］：

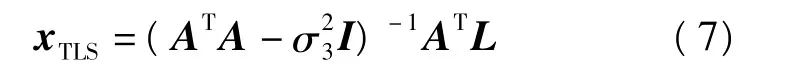
其中σ3為增廣矩陣［A L］的最小特征值。

3 異常點的刪除

在利用地面激光掃描系統對研究對象進行掃描時，由于各種因素影響，如掃描時行人通過、樹木遮擋等，必然使得獲取的點云數據存在異常點。因此為了提高擬合精度，在采用整體最小二乘法解算時，還需要去除點云數據中的異常點，以獲取穩健的平面參數a、b、c的估計值。具體算法如下：

1)利用整體最小二乘法計算a、b、c的初始值;

2)根據計算出的a、b、c值，采用

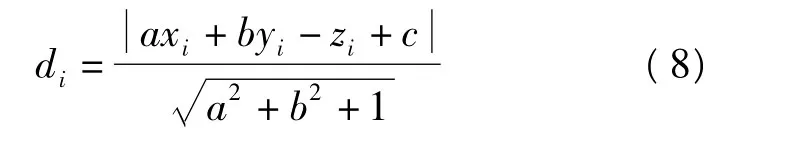
計算每個點至擬合平面的距離di;

3)利用

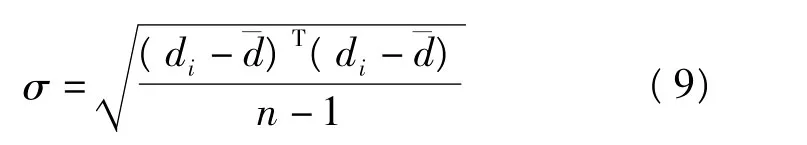
計算距離di的標準偏差。其中：

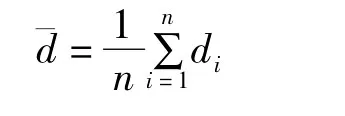
4)當di＞2σ時，此點被認為是異常點，刪除;反之，保留;

5)利用所有保留下來的點通過整體最小二乘重新計算參數a、b、c，即可獲得最佳平面參數。

4 實驗及結果分析

為了驗證本算法的可靠性和穩健性，首先采用仿真數據進行實驗。設要擬合的空間平面方程為

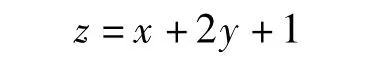
利用Matlab［10］從此平面上隨機抽取1 000個點(圖1)，并通過Matlab編程，利用最小二乘法、特征值法及穩健整體最小二乘法對上述仿真數據進行參數估計，表1為計算結果。

當數據中存在異常值時(人為地使其中的8個點成為異常點(圖2，小圈圈出的表示異常點))的計算結果如表2所示。

通過表1、2可以看出：當數據不存在異常值時，3種方法計算結果基本一致，本文方法精度最高;當數據中存在異常值時，本文方法最準確且精度最高。

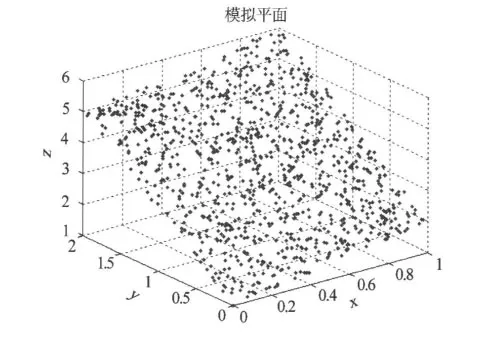
圖1 模擬平面點云數據Fig.1 Simulated plane point clouds

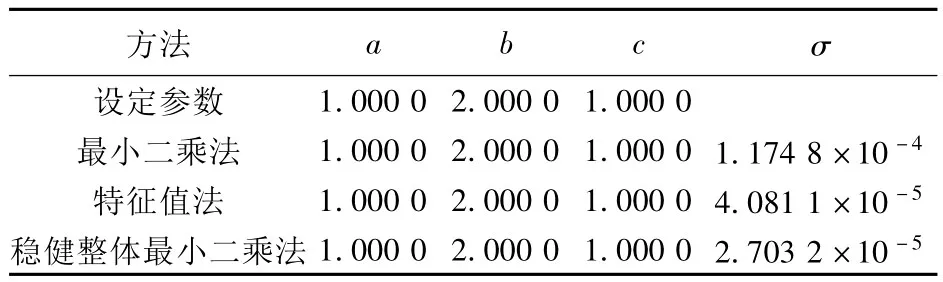
表1 模擬平面參數的設定值及各種方法的參數估值(不含異常值的結果)Tab.1 Parameters of simulated plane and its estimated values(without outliers)

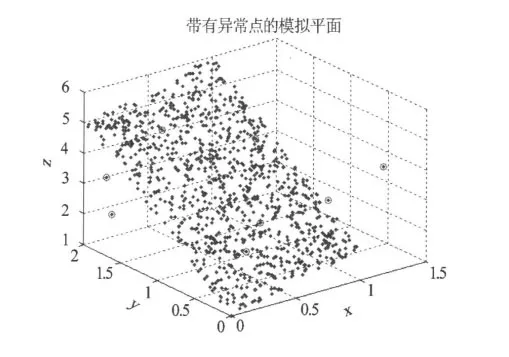
圖2 具有異常點的模擬平面點云數據Fig.2 Simulated plane point clouds with outliers

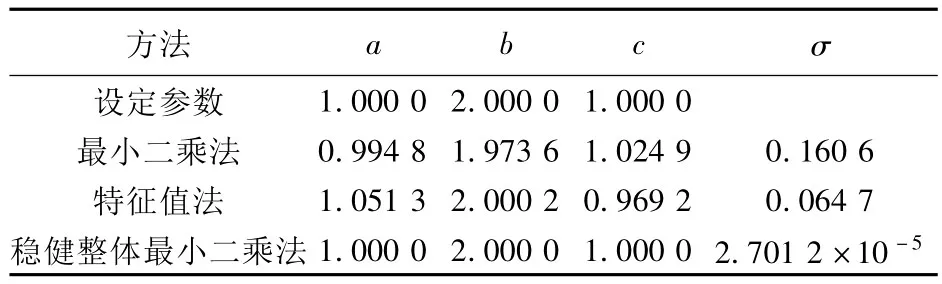
表2 模擬平面參數的設定值及各種方法參數估值(人為加入異常值后的結果)Tab.2 Parameters of simulated plane model and its estimated values(with outliers)

為了進一步說明本文算法的準確性，采用真實點云數據進行計算。該數據為在距離一平面標靶10m處對其進行掃描，掃描結果見圖3。

由圖3可知數據中存在大量的非標靶平面上的點。現利用最小二乘法、特征值法及穩健整體最小二乘法估計標靶的參數，結果見表3。

為了驗證平面參數的正確性，現根據計算出的空間平面參數，計算掃描儀到該平面標靶的距離，結果見表4。

由表4可知，根據穩健整體最小二乘法計算出的結果最接近真實的距離，由此可見，本文方法的計算結果比其他方法所得結果更可靠。

圖3 平面標靶及其點云數據Fig.3 Plane target and its point cloud data

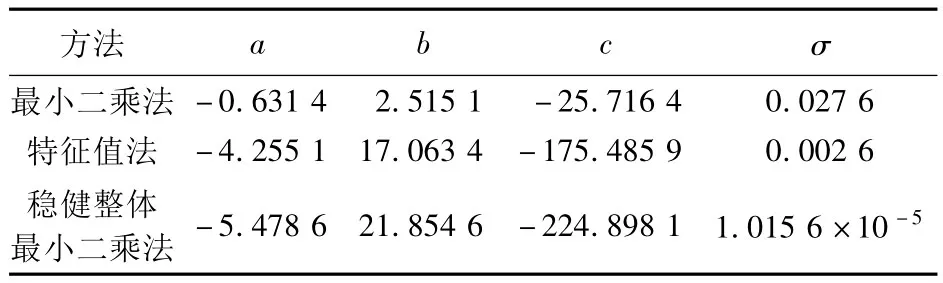
表3 各種方法得到的空間平面參數值Tab.3 Estimated parameters for real plane target obtained with various methods

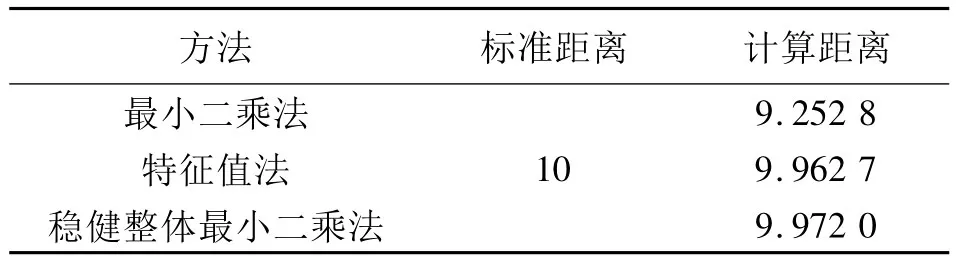
表4 掃描儀到標靶的平面距離(單位：m)Tab.4 Estimated distances between the real target and scanner(unit：m)

5 總結

真實場景中存在大量的平面特征，利用地面三維激光掃描儀對其進行掃描時，獲取的數據中不可避免地存在誤差及異常值。本文在整體最小二乘的基礎上，提出了一種穩健平面擬合方法，并通過實驗與傳統方法進行比較，結果證明了該算法的穩健性和可靠性。該方法不僅適用于從點云數據中擬合平面，也適用于其他包含異常值的數據的平面擬合。

需要說明的是，在進行擬合前，需要對點云數據進行分割，將可能相同特性的點劃分為同一集合再進行擬合。

1 羅德安，等.基于3維激光影像掃描技術的整體變形監測［J］.測繪通報，2005，(7)：40-42.(Luo Dean，et al.Whole object deformation monitoring based on 3D laser scanning technology［J］.Bulletin of Surveying and Mapping， 2005，(7)：40-42)

2 Prabhat K Acharya，et al.Parameter estimation and error analysis of range data［B/OL］.http：//ieee-xplore.ieee.org/xpls/abs_all.jsp?arnumber=12312，2002.8.

3 何文峰，查紅彬.基于平面特征的深度圖像配準［A］.中國人工智能進展［C］.北京：北京郵電大學出版社，2003.(He Wenfeng and Zha Hongbing.Registration of range data based on planar features［A］.Advance in artificial intelligence in China［C］.Beijing：Beijing University of Posts and Telecommunications Press，2003)

4 Wang Caihua，et.al.Comparison of local plane fitting methods for range data［B/OL］.http：//ieeexplore.ieee.org/ xpls/abs_all.jsp?arnumber=990538，2003.4.

5 官云蘭，等.一種穩健的點云數據平面擬合方法［J］.同濟大學學報(自然科學版)，2008，36(7)：981-984.(Guan Yunlan，et al.A robust method for fitting a plane to point clouds［J］.Journal of Tongji University(Natural Science)，2008，36(7)：981-984)

6 Golub G H and Lan Loan F C.An analysis of the total least squares problem［J］.SIAM Journal on Numerical Analysis，1980，17(6)：883-893.

7 Burkhard Schaffrin.A note on constrained total least squares estimation［J］.Linear Algebra and its Application，2006，(417)：245-258.

8 魯鐵定，等.基于整體最小二乘的地面激光掃描標靶球定位方法［J］.大地測量與地球動力學，2009，(4)：102-105.(Lu Tieding，et al.Sphere target fixing of point cloud data based on TLS［J］.Journal of Geodesy and Geodynamics，2009，29(4)：102-105)

9 張賢達.矩陣分析與應用［M］.北京：清華大學出版社，2008.(Zhang Xianda.Matrix analysis and applications［M］.Beijing：Tsinghua University Press，2008)

10 龔劍，朱亮.Matlab 5.X入門與提高［M］.北京：清華大學出版社，2000.(Gong Jian and Zhu Liang.Matlab 5.X introduction and improvement［M］.Beijing：Tsinghua University Press，2000)

ROBUST PLANE FITTING OF POINT CLOUDS BASED ON TLS

Guan Yunlan1)，Liu Shaotang2)，Zhou Shijian1，3)，Zhang Liting1)and Lu Tieding1)

(1)School of Surveying and Mapping Engineering，East China Institute of Technology，Fuzhou 344000 2)Department of Civil Engineering，Henan Institute of Engineering，Zhengzhou 451191 3)Jiangxi Academy of Science，Nanchang330029)

In traditional plane fitting methods for point clouds，people don’t consider errors in data and in coefficients matrix simultaneously，which will result in incorrectness of plane parameters.In order to overcome this shortcoming，a new method for fitting local plane to point clouds was proposed.The method is based on total least squares.In consideration of the errors in all observation data，we tried to delete outliers from point clouds，and thus obtained a robust solution to plane fitting parameter.Analytical experiments based on simulated data and real data were conducted，and comparisons between the method and traditional methods such as least square method and eigenvalue method were also implemented.The results show that the method has the capability to overcome bad influence from outliers，and to increase the reliability of parameters estimation.

point clouds;Total Least Squares(TLS);plane fitting;outliers;robustness

1671-5942(2011)05-0080-04

2011-05-17

國家自然科學基金(40874010);江西省自然科學基金(2008GQC0001，2010GZC0009，2010GZC0008);地球空間環境與大地測量教育部重點實驗室開放基金(10-01-06)

官云蘭，女，1975年生，副教授，博士，主要從事攝影測量與遙感、GIS的教學與科研工作.E-mail：guan8098@163.com

P207

A