規則格網模型轉換為三角網模型的新方法

李功權

(長江大學地球科學學院，湖北 荊州 434023)

規則格網模型轉換為三角網模型的新方法

李功權

(長江大學地球科學學院，湖北 荊州 434023)

在保留重要點法的基礎上，根據GRID與TIN模型的特性，設計了一個新的模板——“方孔錢”模板，此模板考慮了縱、橫、對角3個方向上的情況，還兼顧了以節點為圓心，2倍網格步長度為半徑的圓作為搜索方向。通過對一個在縱向上分布為3個山脊和2個山谷，且山脊與山谷之間有的坡度陡峭，有的坡度平緩的網格數據模型的測試說明，該算法不但很好地保留了關鍵網格點(頂點、凹點)，最大限度地消除了冗余高程點，消除率達50%以上；而且保證了轉換前后模型的精度。

GRID; TIN; 三維可視化; 模板; 數字高程模型

在DEM中，格網模型(GRID)和不規則三角網(TIN)有著各自的優缺點，適用于不同的場合和應用目的[1]。但由于數據的來源格式不一定符合當前的應用和要求，這就有可能需要將GRID模型轉換為TIN模型。目前GRID向TIN的轉換主要有2種算法：①保留重要點法(VIP, Very Important Point)；②啟發丟棄法(DH, Drop Heuristic)。VIP方法在保留關鍵網格點方面(頂點、凹點)最好，但沒有很好的考慮在重構TIN模型時邊選取的一些規則，沒有最大限度的消除冗余點；DH方法在每次丟棄數據點時確保信息丟失最少，但要求計算量大[2]。這2種算法都沒有實現效率與精度的最佳融合。易法令等[3]、朱理等[4]分別根據Delaunay三角形的特點和高程點的法向量來作為選點條件，研究了GRID向TIN的轉換算法，在消除冗余點方面取得了較好的效果，但精度評價只是和ArcInfo提供的算法進行了對比。下面，筆者以最大限度的消除冗余點、保證轉換精度為目標，設計了一種新的模板——“方孔錢”模板，很好的實現了效率與精度的兼容。

1 轉換算法

1)轉換算法選點一般原則 當空間某一點的高程數據能由已知點的高程數據推導時，該高程數據是冗余的,可刪除。為了增加重構三角網時TIN模型的穩定性和規則性，在篩選時遵循了Delaunay三角網重構時的選取方法，也用到了Delaunay三角網的一些特性[5～7]。因此在判斷某一點的高程數據為冗余后，還應判斷刪除該點后在重構TIN模型時還能否滿足Delaunay三角網的特性。

2)模板說明 通過對TIN模型的構網方法與Delaunay三角網的特性研究論證出了2類可刪除高程數據的情況。具體說明如下：

圖1 第1類可刪除的高程點

①第1類可刪除的情況。當A22=(A12+A32)/2；A22=(A21+A23)/2；A22=(A11+A33)/2并且A22=(A13+A31)/2，A22可刪除。如圖1示，當A22點高程數據被刪除后，可構成的TIN模型如圖1(b)，(c)。根據Delaunay三角網的特性三角形的外接圓內不存在其他點[3～7]，圖1(b),(c)是滿足Delaunay三角網要求的。在圖1(b)中A22的高程數據能由A21，A23推導，在圖1(c)中A22的高程數據能由A12,A32推導，因此A22的高程數據可刪除。要求A22=(A11+A33)/2和A22=(A13+A31)/2是考慮到精度的需求。

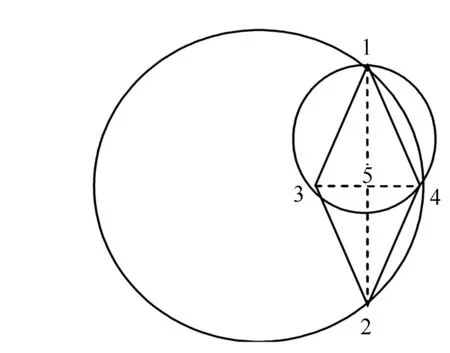
圖2 第2類可刪除的高程點

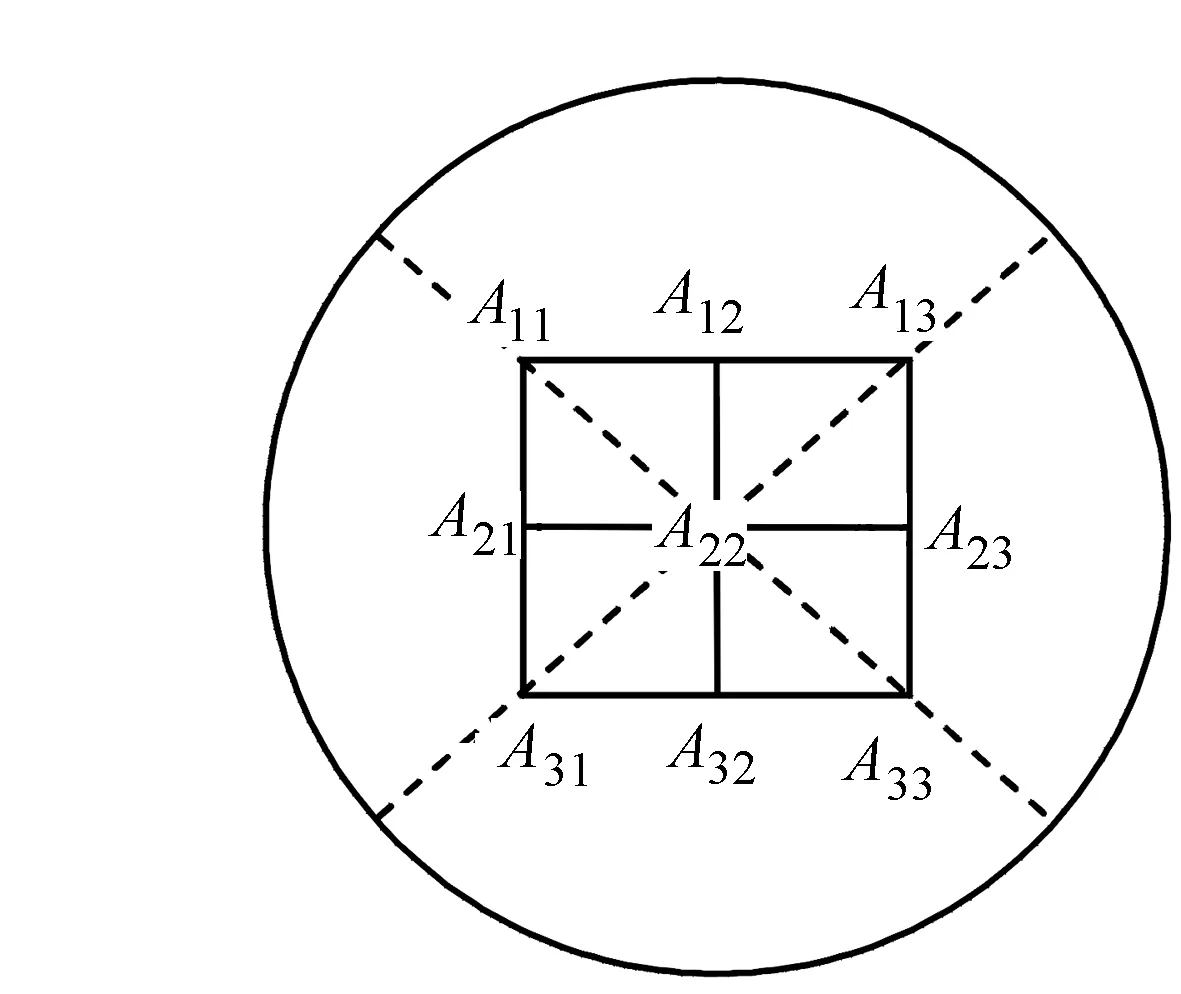
圖3 模板形狀

②第2類可刪除的情況。當A22=(A12+A32)/2并且在模版的圓框內不存在兩點過線段A12A32時；或者當A22=(A21+A23)/2并且在模版的圓框內不存在兩點過線段A21A23時，A22可刪除。如圖2所示，高程點5的值能由高程點3、4的值導出。當刪除點5的高程數據后，在形成Delaunay三角網時可出現12或34兩條線段來實現三角化，如果是12線段來實現三角化則點3在點1、2、4所形成的外接圓內顯然是不滿足Delaunay三角網的特性的，也就是說在這種條件下刪除5號點后在生成TIN模型只會選擇34。而高程點5的值能有34導出。即要求12線段的長度超過34線段的長度時5號點才能刪除。在模板中即要求圓框內不存在過線段3，4的線段。

根據GRID與TIN模型的特性，依據上述分析，可以歸納為模板形狀如圖3所示，其中A11…A33是高程數據在GRID中的保存形式，外圓是以線段A21A23的長度為半徑，以點A22為圓心繪制。

3)精度保證 為了保證轉換過程中模型的精度，在進行第2類情況的判斷時，應先判斷A22是否為“重要點”，所謂重要點是指在第一類情況中刪除了高程點的情況下，那些保留下來的、能推導出已刪除點高程數據的點。如果是重要點則即使滿足條件也不應刪除，不是則可按照上面的判斷條件進行高程點的刪除。

4)算法的靈活性 該模板不僅實現了效率與精度的最佳融合，并且還可根據不同的要求對刪除條件進行調整以達到特定的要求。如精度要求相當高時，可將模板中的外圓去掉。效率要求相當高時，可在高程的比較中采用設置閥值的方法，還可適當的調整模板的外圓大小，以達到最大限度的消除冗余點，提高建TIN模型時的速度。

2 新算法測試及評估

為了檢查新算法的效果，特挑選了一個具有典型特征的網格數據(見圖4(a))，該數據模型在縱向上分布為3個山脊和2個山谷，且山脊與山谷之間有的坡度陡峭，有的坡度平緩。為了方便對比，在VC6.0下調用OpenGL提供的三維圖形軟件開發包(glu32.lib、opengl32.lib、glaux.lib)；將轉換后的數據和Z軸上的屬性值按Delaunay三角網規則構建TIN模型，實現了格網模型和TIN模型的三維可視化(圖4(b))。這樣，不僅有助于分析原始網格模型的典型地形特征，而且還有利于算法之間、模型之間的相互比較和評價。

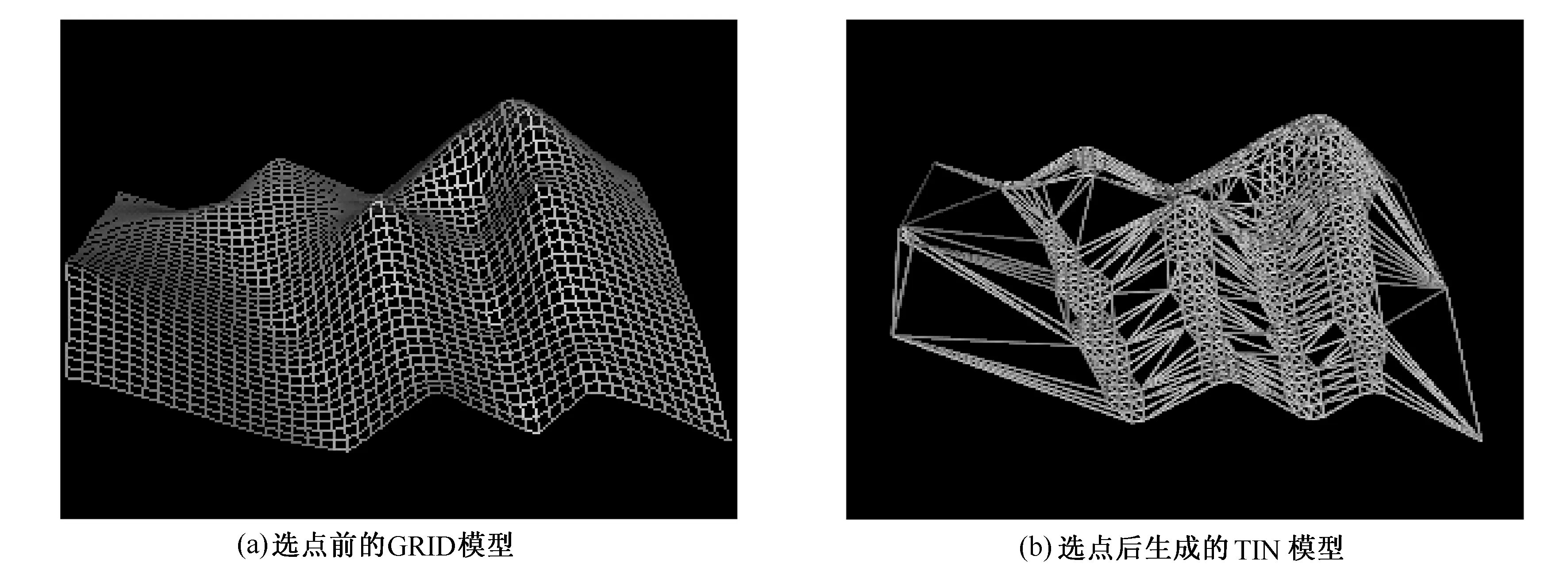
圖4 選點前后模型比較

筆者選擇了保留重要點法中最經典的3×3模板算法與該算法進行了比較，如表1所示。可以看出，隨著GRID模型的網格數目的增加，該算法去掉冗余點的數目越來越多，基本都超過了50%，但3×3模板算法冗余點的消除變化不大。該算法與3×3模板算法對比可以看出，該算法冗余點消除的百分比多達10%以上。在精度比較過程中，選擇了表1中的第3組數據進行轉換前后的比較(圖5)，從圖5分析得到，該算法不但在保留關鍵網格點方面(頂點、凹點)相當好，而且在坡度平緩區域中大大消除了冗余點。

表1 新算法與3×3模板比較

3 結 語

隨著DEM模型在社會生活中的廣泛應用，GRID和TIN模型的相互轉化也會得到進一步的深入研究。筆者根據GRID模型和TIN模型的特點，以保留重要點法為基礎，提出基于“方孔錢”模板的GRID向TIN的轉換算法。通過在三維可視化的環境下的測試表明，該算法不但很好地保留了關鍵網格點(頂點、凹點)，而且最大限度地消除了冗余高程點，冗余高程點的消除率達50%以上，而且保證了轉換前后模型的精度。可見，該算法有較高的實用價值。

[1]周啟鳴, 劉學軍. 數字地形分析[M]. 北京: 科學出版社, 2006：57-62.

[2]JAY Lee. Compparison of existing methods for building triangular irregular netwoek models of terrain from grid digital elevation models[J]. International Journal Geographical Information Systems，1991, 5(3): 267-285.

[3]易法令, 韓德志, 謝云. GRID轉換為TIN的選點算法[J]. 計算機工程, 2003,29(11):62-63.

[4]朱理, 胡超. 一種有效的規則網格到不規則三角網的轉換算法[J]. 計算技術與自動化, 2006,25(2):67-70.

[5]劉學軍, 符鋅砂, 趙建三. 三角網數字地面模型快速構建算法研究[J]. 中國公路學報, 2000, 13(2): 31-36.

[6]Tsung-Pao Fang and Les A. Piegl. Delaunay Triangulation Using a Uniform Grid[J]. IEEE Computer Graphics &Applications，1993,13(3):36-47.

[7]Lewis B A, Robinson J S. Triangulation of Planar Regions with Applications [J]. The Computer Journal, 1978, 21(4): 324-332.

[編輯] 洪云飛

10.3969/j.issn.1673-1409.2011.04.022

TP311

A

1673-1409(2011)04-0068-03