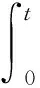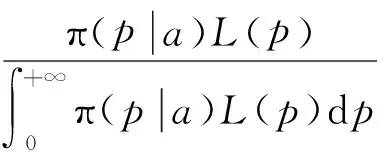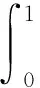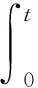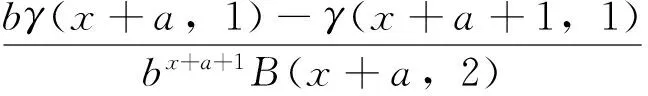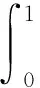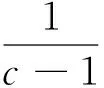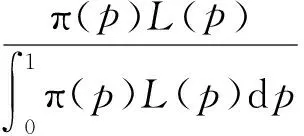復合LINEX對稱損失函數下幾何分布參數估計
李俊華
(鄖陽師范高等專科學校數學系,湖北 十堰 442000)
復合LINEX對稱損失函數下幾何分布參數估計
李俊華
(鄖陽師范高等專科學校數學系,湖北 十堰 442000)
在幾何分布可靠度的先驗分布為其冪分布時,給出了幾何分布可靠度在復合LINEX對稱損失函數下的Bayes估計和多層Bayes估計。
幾何分布;損失函數; Bayes估計;多層Bayes估計
許多壽命離散型的產品,其壽命服從幾何分布,因此對幾何分布的可靠性分析具有理論和實際應用價[1,2]。在貝努里實驗里,若p為每次實驗成功的概率,如果進行了x+1次實驗,前x次實驗成功且第x+1次不成功(或失敗)的概率為:
P(X=x)=px(1-p)x=0,1,2,… 0 (1) 則稱隨機變量X服從幾何分布,其中p為幾何分布的可靠度(或成功概率)。 1975年Varian提出了LINEX損失函數[3]: Lb(θ,δ)=e-b(θ-δ)+b(θ-δ)-1 (b>0) 式中,δ為參數θ的估計;b是該損失函數的尺度參數。當b≠0時LINEX損失函數是一類非對稱損失函數。文獻[4]提出了復合LINEX對稱損失函數,表達形式如下: L(θ,δ)=Lb(θ,δ)+L-b(θ,δ)=e-b(θ-δ)+eb(θ-δ)-2 (b>0) (2) 下面,筆者在復合LINEX對稱損失函數下給出了幾何分布可靠度的多層Bayes估計[5]。 證明在損失函數L(θ,δ)=e-b(p-δ)+eb(p-δ)-2(b>0)下,令δ(x)為p的任一Bayes估計, 則其Bayes風險為R(δ)=E(L(p,δ))=E(E(L(p,δ)|x))。欲使R(δ)最小,只需E(L(p,δ)|x)幾乎處處達到最小,由于E(L(p,δ)|x)=E((e-b(p-δ)+eb(p-δ)-2)|x),所以只需證明E((e-b(p-δ)+eb(p-δ)-2)|x)最小,因為δ非負,則最小值不會是0或無窮遠點。 記: h(δ)=E((e-b(p-δ)+eb(p-δ)-2)|x)=eb δE(e-bp|x)+e-b δE(ebp|x)-2 對h(δ)關于δ求導并令其為0,即h′(δ)=beb δE(e-bp|x)-be-b δE(ebp|x)=0,解得: 又因為h(δ)關于δ是嚴格凸函數,故δB(x)是其唯一的極小值點,進而得到Bayes估計是唯一的。 若幾何分布可靠度p的先驗分布為冪分布,其密度函數為: π(p|a)=apa-1(0 (3) 則此時θ的Bayes估計由以下定理給出。 定理2取式(3)為p的先驗分布,在損失函數(2)下,p的Bayes估計為: 證明對幾何分布,取p的先驗分布為式(3),而p的似然函數為L(p)=px(1-p),根據Bayes定理,p后驗密度為: 從而有: 同理可以計算: 所以在復合LINEX對稱損失函數下p的Bayes估計為: 引理1在給定的Bayes決策中,對給定的先驗分布π(θ),θ的Bayes的δB(x)是唯一的,則它是容許的。 由于幾何分布可靠度估計在復合LINEX對稱損失函數下是嚴格凸的,其Bayes估計必是唯一的,由引理可知該估計是可容許的。 (4) 定理3對幾何分布,若p的多層先驗分布由(4)給出,則在復合LINEX對稱損失函數下p的多層Bayes估計為: 證明根據Bayes定理,p的多層后驗密度為: 則在復合LINEX對稱損失函數下p的多層Bayes估計為: 其中: [1]韓明,崔玉萍.幾何分布的可靠度估計[J]. 運籌與管理,2001,10(4):35-38. [2]韓明. 多層先驗分布的構造及其應用[J].運籌與管理,1997,6(3):32-40. [3]韋程東,韋師,蘇韓. 復合LINEX對稱損失下Pareto分布形狀參數的E-Bayes估計及應用[J].統計與決策,2009,(17):7-9. [4]張睿. 復合LINEX損失下的參數估計[D].大連:大連理工大學,2007. [5]茆詩松.貝葉斯統計[M].北京:中國統計出版社,1999. [編輯] 洪云飛 10.3969/j.issn.1673-1409.2011.04.004 O213.2 A 1673-1409(2011)04-0011-031 p的Bayes估計
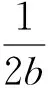
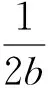
2 p的多層Bayes估計