GD2308高速加固縫紉機壓腳有限元建模與分析

劉 銀， 初 嘉 鵬， 余 明

（1.大連工業(yè)大學(xué) 機械工程與自動化學(xué)院，遼寧 大連 116034；2.大連大富基縫紉機有限公司，遼寧 大連 116034）

0 引 言

目前工業(yè)縫紉機在不斷向多功能、高速方向發(fā)展的同時，其振動和噪聲問題也日益突出，亟須解決。結(jié)構(gòu)振動會產(chǎn)生噪聲、影響壽命等不良影響，振動結(jié)構(gòu)的減振降噪設(shè)計是相關(guān)工程中結(jié)構(gòu)設(shè)計的重要內(nèi)容之一。用有限元法和邊界元法對結(jié)構(gòu)進行振動和聲學(xué)進行數(shù)值仿真在工程中已廣泛應(yīng)用［1-2］，以此為基礎(chǔ)用優(yōu)化方法在結(jié)構(gòu)設(shè)計階段對結(jié)構(gòu)進行修改以減小結(jié)構(gòu)振動以降低噪聲一直是人們關(guān)注的研究課題之一［3-5］。有限元技術(shù)的日益成熟和發(fā)展，為控制結(jié)構(gòu)的固有頻率與振型提供了理論基礎(chǔ)。根據(jù)模態(tài)分析理論，一般大型工程結(jié)構(gòu)，只需計算前幾階較低的固有頻率和振型，因為低階振動對結(jié)構(gòu)的動力影響最大。本文采用有限元軟件對高速加固縫紉機壓腳進行模態(tài)分析，并對其動態(tài)性能進行評價。

1 有限元模型的建立

建模是基于梁單元理論和薄板理論，采用彈簧單元模擬空氣懸架的作用，輔以三維質(zhì)量單元對玻璃等建模中沒有考慮的載荷進行加載模擬。有限元建模的總則是根據(jù)工程分析的實際要求，建立合適的，能模擬實際工況的有限元模型。在不影響計算精度的前提下對模型進行適當(dāng)?shù)暮喕瑢⒖s短建模時間，而且可以突出主要問題。本文所建立的高速加固縫紉機的壓腳的有限元模型中，簡化了結(jié)構(gòu)，忽略了過渡圓角、倒角、工藝孔等影響，將其視為表面圓整光滑的結(jié)構(gòu)。

2 模態(tài)分析理論基礎(chǔ)

模態(tài)分析就是利用系統(tǒng)固有振型（或模態(tài)）的加權(quán)正交性進行坐標(biāo)變換，使系統(tǒng)在新的模態(tài)坐標(biāo)中的運動方程組變成一組互不耦合彼此獨立的方程，以便求出系統(tǒng)的模態(tài)參數(shù)。由此可以看出模態(tài)計算過程的實質(zhì)是一種坐標(biāo)變換，其目的是為了解除方程的耦合，便于求解。一般來說由于高階模態(tài)比低階模態(tài)加權(quán)系數(shù)小得多，通常只選取前n階模態(tài)進行疊加，即可達(dá)到足夠的精度。

通常，無阻尼自由振動的矩陣方程可以寫為：

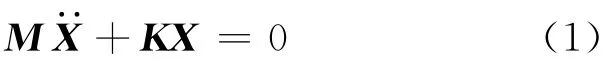
式中，M 為機殼有限元模型的總體質(zhì)量矩陣，是一正定矩陣：K 為總體剛度矩陣，此處由于所有剛體自由度全被約束掉，因此一也是一正定矩陣；X為振動的位移向量。

求解式（1）特征頻率方程，即

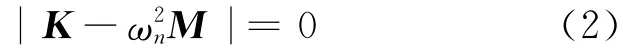
可得到模型的各階固有頻率ωni（i=1，2，…，n。其中，n為有限元模型的自由度數(shù)）。

當(dāng)固有頻率為特征方程式（2）的重根時，將其代入方程

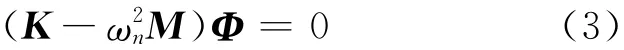
可解得對應(yīng)模態(tài)振型｛Φ｝。

當(dāng)ωni為特征方程式（2）的單根時，將其代入特征矩陣方程

求出該特征矩陣的伴隨矩陣

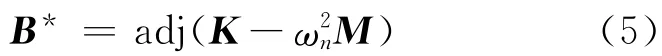
則該伴隨矩陣的任一非零列向量即為固有頻率ωni所對應(yīng)的振型。上述過程在數(shù)學(xué)上稱為多自由度廣義特征值問題。定義振型矩陣Φ = ｛Φ1，Φ2，…，Φn｝，系統(tǒng)的特征值是ω21，ω22，…，ω2n，所對應(yīng)的特征向量用Φ1，Φ2，…，Φn表示；顯然，Φi滿足方程：KΦi=ω2nMΦi（i=l，2，…，n）合并寫為KΦ=MΦω2，兩邊左乘ΦT，則ΦTKΦ =ΦMΦω2，即：

其中，K=ΦTKΦ，M=ΦTMΦ 分別為主坐標(biāo)剛度陣和主坐標(biāo)質(zhì)量陣，二者都是對角陣。

在結(jié)構(gòu)動力學(xué)中，Φi稱之為機構(gòu)的振型或模態(tài)，ωi為各階模態(tài)頻率。對于工程中的成百上千個，甚至上萬的自由度情況，上述過程可以利用數(shù)值方法求解，對于n自由度系統(tǒng)來說，有n個自振頻率和對應(yīng)的n 個振型。在CATIA 和ANSYS軟件中可以求解模型的運動模態(tài)，若模型為剛?cè)狁詈系模€可以反應(yīng)結(jié)構(gòu)模態(tài)。

3 有限元計算模態(tài)振型的結(jié)果和分析

采用CATIA 建立壓腳的三維實體結(jié)構(gòu)模型并完成網(wǎng)格劃分、單元屬性設(shè)置、材料屬性設(shè)置（表1）等前處理步驟，得到如圖1所示的有限元模型，再導(dǎo)入到ANSYS中，施加載荷和約束進行模態(tài)分析，求得前200階的固有頻率和振型。表2是壓腳對應(yīng)的前10階固有頻率。

表1 壓腳的材料屬性Tab.1 Material property of the presser foot

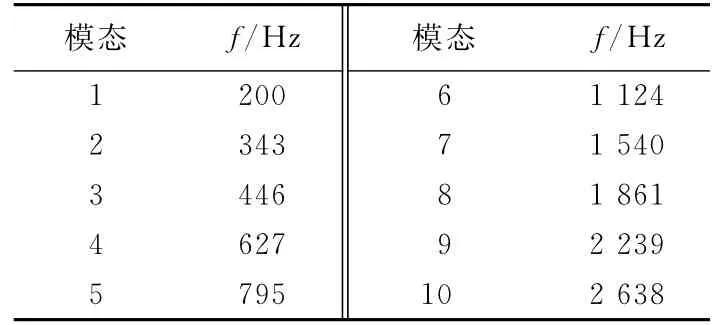
表2 模態(tài)分析的計算結(jié)果Tab.2 Modal analysis results

圖1 壓腳有限元模型Fig.1 Finite element model for presser foot

由振型圖2可見，壓腳的振動形態(tài)多樣，集中表現(xiàn)為彎曲振動和扭轉(zhuǎn)振動。第一階振型表現(xiàn)為繞z軸的扭轉(zhuǎn)變形振動，第二階振型表現(xiàn)為繞x軸的彎曲變形振動，第三階振型表現(xiàn)為沿y 軸的搖擺變形振動，第四階振型主要表現(xiàn)為在繞x 軸的彎曲變形振動，第五階振型主要表現(xiàn)為繞z 方向的扭轉(zhuǎn)變形振動，第六階振型主要表現(xiàn)為繞y和z 軸方向的扭轉(zhuǎn)變形振動。振型反映了在振動模態(tài)下，結(jié)構(gòu)各個部位之間位移的相對值。從振型圖上可以找出振動模態(tài)下的結(jié)構(gòu)振動響應(yīng)的表現(xiàn)形態(tài)（彎曲變形、扭轉(zhuǎn)變形或者彎曲扭轉(zhuǎn)的復(fù)合變形等），同時也能發(fā)現(xiàn)振動時節(jié)點的位移等，為確定結(jié)構(gòu)動態(tài)破壞部位提供依據(jù)，從而預(yù)知結(jié)構(gòu)設(shè)計的薄弱環(huán)節(jié)，為減振降噪與結(jié)構(gòu)的優(yōu)化設(shè)計提供參考。

壓腳的模態(tài)分析屬于基本振動問題，模型的規(guī)模相對較大，同時由于過高頻率的振動對整機的振動貢獻(xiàn)不大且高階振型疊加嚴(yán)重且局部振動較多，而低階振動對整機的振動影響最大，故本文僅取前10階振型進行分析。

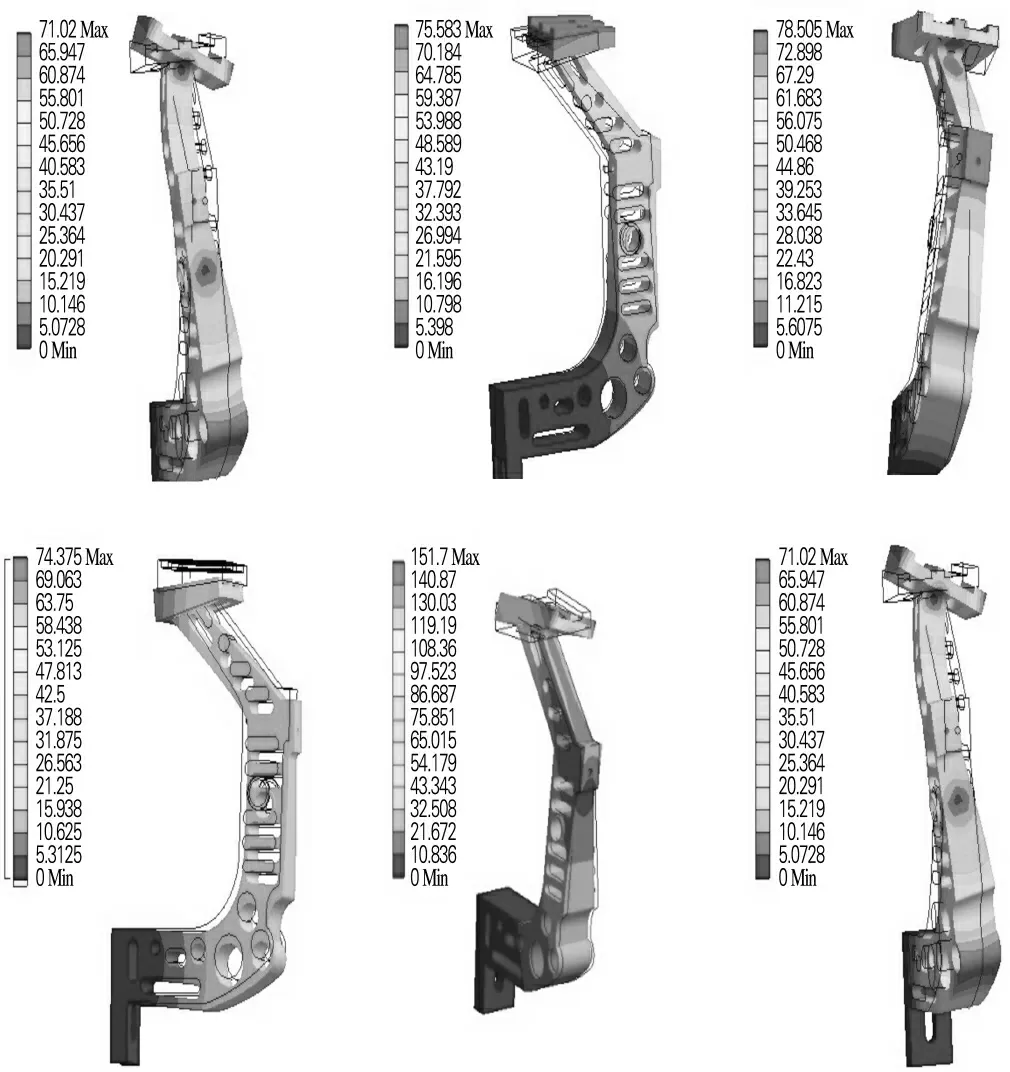
圖2 壓腳的前6階振型Fig.2 The first six modes of the presser foot

4 結(jié) 論

工業(yè)縫紉機由于其結(jié)構(gòu)異常復(fù)雜，采用試驗?zāi)B(tài)方法進行模態(tài)分析具有一定難度，而且該方法周期長、工作量大、成本高，不利于進行控制和評價，因而限制了試驗?zāi)B(tài)分析在縫紉機上的應(yīng)用。本文以高速加固縫紉機為例，根據(jù)相關(guān)技術(shù)資料對壓腳進行了動態(tài)性能進行評價，由于縫紉機壓腳設(shè)計、分析、計算的試驗性很強，所以計算結(jié)果相對于實際情況存在一定的偏差，但總的來說，分析計算得到的結(jié)果基本符合理論計算值，所以分析的過程和結(jié)果對壓腳的優(yōu)化設(shè)計及工業(yè)縫紉機的減振降噪具有正確的指導(dǎo)作用。

［1］張亮，袁兆成，黃震.流固耦合有限元法用于油底殼模態(tài)計算［J］.振動與沖擊，2003，22（4）：100-102.

［2］梁新華，朱平，林忠軟，等.基于有限元法和邊界元法的輕量化車身聲學(xué)分析［J］.上海交通大學(xué)學(xué)報，2006，40（1）：177-180.

［3］楊德慶，柳擁軍.薄板減振降噪的拓?fù)鋬?yōu)化設(shè)計［J］.船舶力學(xué)，2003，7（5）：91-96.

［4］張軍，兆文忠，謝素明，等.結(jié)構(gòu)-聲場耦合系統(tǒng)聲壓響應(yīng)優(yōu)化設(shè)計研究［J］.振動工程學(xué)報，2005，18（4）：519-523.

［5］MARBURG S.A general concept for design modication of shell meshes in structural-acoustic optimization.Part I：formulation of the concept［J］.Finite Elements in Analysis and Design，2002，38（7）：725-735.