隨機線元落入緩沖區內的概率分布函數研究

苗則朗,馮永興,張書畢,張秋昭

(1.中國礦業大學環境與測繪學院,江蘇徐州 221008;2.江蘇省資源環境信息工程重點實驗室,江蘇徐州 221008)

隨機線元落入緩沖區內的概率分布函數研究

苗則朗1,2,馮永興1,張書畢1,張秋昭1

(1.中國礦業大學環境與測繪學院,江蘇徐州 221008;2.江蘇省資源環境信息工程重點實驗室,江蘇徐州 221008)

通過仿真計算出隨機線元落入其“真實值”緩沖區內的比例,并采用柯氏檢驗法對其進行分布擬合檢驗,得出隨機線元落入緩沖區內的比例服從正態分布的結論,從而完善線元誤差不確定帶模型。

隨機線元;緩沖區;正態分布;柯氏檢驗法

一、引 言

線狀地形物的特征一般包括長度和曲率,通常線狀地形物的真實位置不容易獲得或者獲得的方式比較困難[1],因此不容易對線元整體精度作出評價。有關線狀地形物精度評價目前已有多種模型。Perkal于 1956年首先提出了應用 Epsilon帶模型來建立線元不確定性模型[2],圍繞“真實”的位置建立寬度相等的緩沖區,比較測量值與“真值”之間的關系;Blakemore定義了點與線段的緩沖區之間的五種位置關系:絕對在、有可能在、模棱兩可、可能不在、絕對不在[3];Skidmore和 Turner通過查找測量與參考線元之間的數目估計線元的精度[4];Goodchild和Hunter利用隨機線元落入緩沖區內的比例評價隨機線元的精度[5];Tveite、Langass和張永彬等通過緩沖區疊置分析,評價測量數據精度[6-7]。但以上方法均假設參考線元與測量線元之間不存在偏移,僅考慮方差的影響。為克服以上方法的不足,Joon Heo等在考慮偏移、方差的綜合影響下,提出了非線性最小二乘方法[1],并將該方法應用于海岸線退化研究[8]。

以上模型與方法,均直接假設隨機線元落入緩沖區內的比例服從高斯正態分布,但沒有給出具體的原因或者推導過程,體系稍欠完善。本文基于計算機仿真和分布擬合檢驗的方法,采用柯爾莫戈羅夫(KolmogorovA N)檢驗法對假設的正態分布進行分布擬合檢驗,給出了隨機線元落入緩沖區內的比例服從高斯正態分布的結論及證明過程。

二、誤差函數及柯氏檢驗法

在數學中,誤差函數 erf(x)(也稱為高斯誤差函數)是一個特殊的函數 (非初等函數),在概率、統計、材料科學和偏微分方程等領域廣泛應用。erf(x)定義為

誤差函數與標準正態分布累積函數 (記為Φ)基本相同,可以通過比例和旋轉運算等同。即

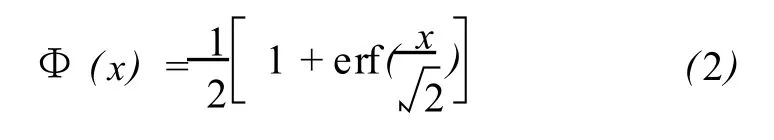
柯氏檢驗法由前蘇聯數學家柯爾莫戈羅夫首先提出,對于連續型的隨機變量,柯氏檢驗法較χ2檢驗法更好。設 X的分布函數 F(x)是未知的;X1,…,Xn是樣本;F0(x)是給定的某個分布函數;作如下假設

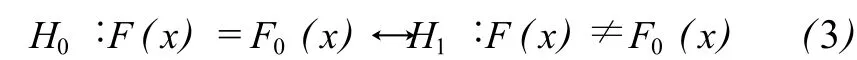
首先從樣本出發求出經驗分布函數 Fn(x),計算分歧度

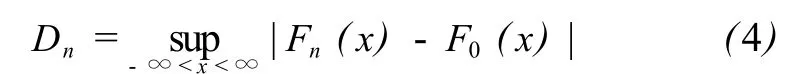
取否定域為

當計算出分歧度 Dn的值小于臨界值λ時,則接受 H0。臨界值λ的取值可以由柯爾莫戈羅夫檢驗臨界值表查知[9]。

三、模擬步驟及分布擬合分析

1.模擬步驟

隨機線元及其使用“真實值”建立的緩沖區示意圖如圖 1所示,隨機線元的分布受偏移和方差的影響,文獻[1]論述了偏移和方差對隨機線元分布的影響。綜合考慮偏移和方差的影響,得出計算機仿真的步驟如下:

1)生成隨機線元。模擬的點分別為 Z1、Z2,并假設 Z1、Z2相互獨立。其分布依次為

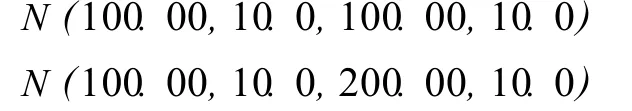
利用Matlab生成上述兩組隨機點,連接兩個隨機點,即得到該線段一組隨機線元。

2)圍繞“真實”線段建立緩沖區。

3)計算隨機線元落入緩沖區內的比例

4)采用蒙特卡羅方法重復以上三個步驟10 000次,將平均值作為該緩沖區帶寬下隨機線元落入帶寬為緩沖區內的比例。

5)以一定的步長(如 0.5 m)增加緩沖區帶寬,重復以上四個步驟,得到一系列不同緩沖區帶寬下隨機線元落入緩沖區內的比例。

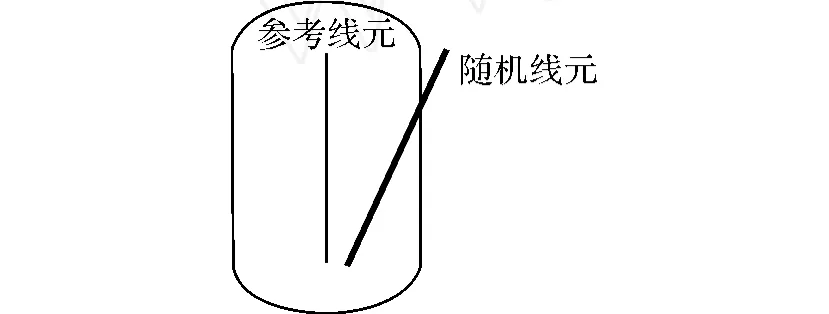
圖1 隨機線元落入緩沖區示意圖

2.模擬結果

隨機線元落入緩沖區內的長度與隨機線元長度的比值如表 1所示;隨機線元落入緩沖區內的比例曲線圖如圖2所示。

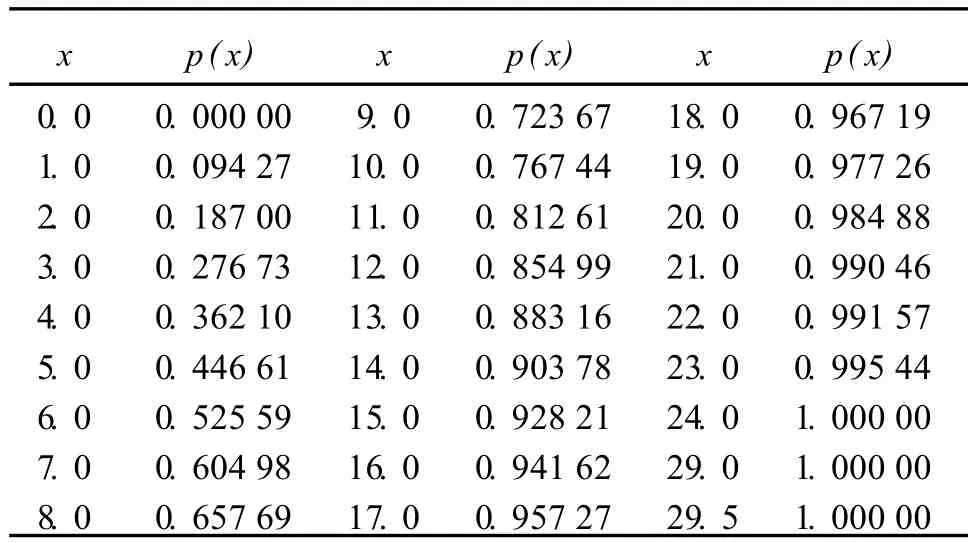
表 1 隨機線元落入緩沖區內的比例

從圖 2中可以發現隨機線元落入緩沖區內的比例曲線圖與誤差函數 erf(x)曲線圖很接近,為了驗證,采用柯氏檢驗法進行假設檢驗。

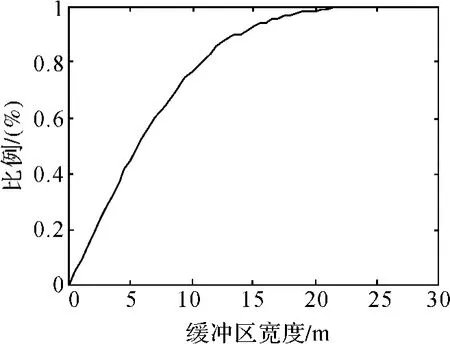
圖 2 隨機線元落入緩沖區內的比例

3.分布擬合檢驗

采用柯氏檢驗法進行假設檢驗。從圖 2可以看出,該曲線的形態與正態分布的誤差函數曲線相似,因此作如下假設

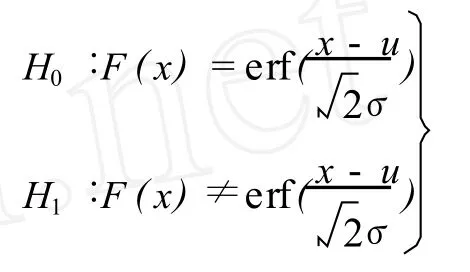
參數μ、σ的最大似然估計值

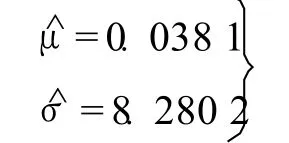
計算分歧度Dn

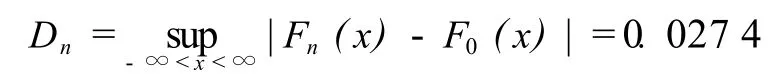
計算臨界值λ

可知

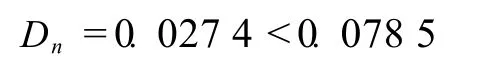
故認為 H0成立。因此,隨機線元落入“真實值”緩沖區內的比例服從高斯正態分布的誤差函數。

四、結果分析

本文通過計算機仿真,驗證了隨機線元落入緩沖區內的比例與正態分布有著密切的聯系即其比例符合正態分布的誤差函數,從體系上完善了 Epsilon帶的應用。但文章不足之處在于:①模擬分析是在假設線元端點分布獨立的情況下研究的,可以推廣到誤差相關的一般情形;②研究對象主要是線元,樣本量較小,可以推廣至折線、曲線等更加一般的情況,這是下一步工作的重點。

[1] JOON H,J IN W K,J I S P,et al.A New Line Accuracy Assess ment Methodology Using Nonlinear Least Squares Estimation[J].Journal of Surveying Engineering,2008, 134(1):13-20.

[2] PERKAL J.On Epsilon Length[J].Bulletin de l′Academic Polonaise des Sciences,1956(4):399-403.

[3] BLAK MORE M.Generalization and Error in Spatial Databases[J].Cartographica,1984,21(2-3):131-139.

[4] SK IDMORE A K,TURNER B J.Map Accuracy AssessmentUsingLine Intersect Sampling[J],Photogrammetric Engineering and Remote Sensing,1992,58(10): 1453-1457.

[5] GOODCH ILD M F,HUNTER G J.A Simple Positional AccuracyMeasure forLinear Features[J].International Journal on GeographicalInfor mation Science,1997, 11(3):299-306.

[6] TVEITE H,LANGASS S.An Accuracy Assess ment Method for Geographical Line Datasets Based on Buffering[J]. International Journal of Geographical Infor mation Science,1999,13(1):27-47.

[7] 張永彬,范愛民.基于誤差熵不確定帶的空間數據質量評價指標 [J].河北理工學院學報,2002(2): 121-127.

[8] JOON H,JUNG H K,J IN W K.A New Methodology for Measuring Coastline Recession Using Buffering and NonlinearLeast Squares Estimation[J]. International Journal of Geographical Information Science,2009,23(9): 1165-1177.

[9] 陳家鼎,孫山澤,李東風.數理統計學講義[M].北京:高等教育出版社,2006:132-135.

Research on Probability D istribution Function of Random L ine within the Buffer Zone

M IAO Zelang,FENG Yongxing,ZHANG Shubi,ZHANGQiuzhao

0494-0911(2011)02-0029-02

P208

B

2010-05-07

苗則朗(1988—),男,安徽碭山人,博士生,主要研究方向為地理信息系統算法及遙感圖像處理及模式識別。