分形相對滲透率計算方法
毛 鑫,馮文光,楊 騫,謝 爽,鄭 麗,張維錦
(1.成都理工大學能源學院,四川成都 610059;2.中國石化西北油田分公司塔河采油一廠;3.中國石油大慶油田有限責任公司第六采油廠;4.中國石化江漢石油管理局井下測試分公司)
分形相對滲透率計算方法
毛 鑫1,馮文光1,楊 騫2,謝 爽1,鄭 麗3,張維錦4
(1.成都理工大學能源學院,四川成都 610059;2.中國石化西北油田分公司塔河采油一廠;3.中國石油大慶油田有限責任公司第六采油廠;4.中國石化江漢石油管理局井下測試分公司)
受儲層非均質性和實驗誤差的影響,巖心實驗得到的相對滲透率曲線很難代表整個油藏的相滲特征。文中根據油田生產數據結合分形理論計算得出油水兩相相對滲透率,從而修正實驗得到的相對滲透率曲線。通過具體的油藏實例,應用分形理論得到相滲曲線計算含水率與油田實際生產中的含水率規律符合性好,表明該方法能提高巖心實驗得到相對滲透率曲線的可靠性。
相對滲透率曲線;分形維;生產數據
相對滲透率曲線資料是油藏工程和油藏數值模擬計算中的重要參數。在缺乏該資料的情況下,如何利用生產資料來求得該數據,并且保證求得數據的可靠性,具有很重要的實際意義。本文建立了含水率和分形維的關系,從而推導出相對滲透率,并且驗證了該方法的可行性。
1 分形維數學模型的建立
根據前人建立的分形維模型,得到潤濕相和非潤濕相求分形維數值的數學公式如下[1-5]:

式中:Kr0、Krw——非潤濕相、潤濕相的相對滲透率,10-3μm2;SD——有效潤濕相飽和度;Df——維度;Sw——含水飽和度;Swi——束縛水飽和度;Np——累計產量;N——地質儲量。
筆者將(2)式修正為:

2 公式的推導
首先,根據生產數據計算出含水率:


根據(1)、(5)式可以求得含水飽和度SD,再根據(10)式,帶入生產數據擬合得到X,從而求得Df,再分別帶入(1)、(5)式求得Kr0、Krw的值,從而得到了不同飽和度下的相對滲透率。
以上式中:Qw——產水量,m3;Q0——產油量,m3;μw——水粘度,mPa·s;μ0——油粘度,mPa·s;fw——含水率,小數;Df——維度,小數。
3
實例計算分析
河南某油田某注水開發砂巖油藏基本參數包括:石油地質儲量為838.48×104m3,地層油的粘度為1.7 mPa·s,地層水粘度0.289 mPa·s,束縛水飽和度0.2676,生產數據見表1某油田的實際生產數據[5]。

表1 某油田的實際生產數據
根據(10)式擬合得到(見圖1生產數據擬合結果圖):X=-1.911 4,R2=0.998 7,Df=2.42,從而得到不同飽和度下的相對滲透率(表2、圖2)。為了驗證本文計算方法的正確性和合理性,預測出不同采出程度下含水上升率規律和含水率(圖3、圖4)。由圖可知:在油田進入高含水階段,采出程度大于0.25后,利用本文的方法計算得到的含水率和實際數據吻合的相當好,證明了該方法計算的相滲曲線的正確性,能夠代表油藏的整體相滲特征[1,5]。

圖1 生產數據擬合結果
4 結論
(1)推導出了一種計算相滲曲線的新方法,適用范圍更廣。
(2)實例應用表明,理論和實際吻合的相當好,該方法準確性較高。

表2 不同飽和度對應的相對滲透率
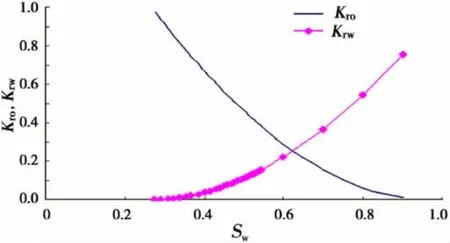
圖2 理論和實際相對滲透率對比

圖3 理論和實際含水率的對比

圖4 含水上升率的對比曲線
(3)因該方法應用的是油田級別的動態數據,且運用的是整個生產時間段的數據擬合求得的相對滲透率,因此得出的相對滲透率較實驗測定的相對滲透率更具有整體性和代表性。
[1] 馮文光.油氣滲流力學基礎[M].北京:科學出版社,2007:193-201.
[2] 謝和平.線性分形維在物理學中的應用[J].自然雜志,1987,12(6):411-414.
[3] 楊露,馮文光,李海鵬.毛管壓力曲線與相滲曲線的分形轉化的相互實現[J].斷塊油氣田,2008,15(2):64-66.
[4] 羅蜇潭.油層物理[M].北京:地質出版社,1986:22-36.
[5] 李克文,秦同洛.分維幾何及其在石油工業中的應用[J].石油勘探與開發,1990,17(5):109-114.
TE312
A
1673-8217(2011)06-0090-02
2011-04-25;改回日期:2011-08-29
毛鑫,1986年生,成都理工大學能源學院在讀研究生,主要研究方向為油氣田開發及油氣藏數值模擬。
彭剛

