基于ANSYS的壓力容器表面雙凹坑干涉效應分析
高 宇,王茂廷,林國慶,海 軍
(遼寧石油化工大學 機械工學院,遼寧 撫順 113001)
基于ANSYS的壓力容器表面雙凹坑干涉效應分析
高 宇,王茂廷,林國慶,海 軍
(遼寧石油化工大學 機械工學院,遼寧 撫順 113001)
針對含有凹坑的壓力容器強度降低這一問題展開分析計算,利用有限元 ANSYS軟件計算其最大應力,并分析雙凹坑間的應力集中干涉效應對壓力容器的影響。通過對數據的分析可知沿環向排列的雙凹坑當兩凹坑相交時,應力集中系數小于單個凹坑應力集中系數,對于安全有利。軸向排列的雙凹坑當兩凹坑相交時,應力集中系數大于單個凹坑應力集中系數。所以軸向排列的雙凹坑更危險。
凹坑;壓力容器; 有限元; 干涉效應
在石化設備中,凹坑是常見的一種壓力容器體積型缺陷。它可能是材料本身含有的,也可能是在加工過程中產生的,多數是由于長期腐蝕而形成的表面凹坑。凹坑的存在,不僅造成應力集中,而且可能由于疲勞載荷作用而萌生裂紋,威脅壓力容器的安全運行,甚至誘發產生壓力容器的泄漏或破裂,造成財產和人員的傷亡[1]。隨著全球經濟和科學技術的飛速發展,有限元數值模擬軟件大量應用于生產設計中[2]。本文利用有限元ANSYS軟件在對單個凹坑應力分析的基礎上,主要對雙凹坑之間干涉效應及應力分布和應力集中現象進行研究。
1 凹坑的應力分布
表面凹坑問題屬于三維裂紋問題,用數學方法處理比較復雜,其應力強度因子一般采用近似公式估算方法處理。本文利用有限元ANSYS軟件對壓力容器表面凹坑進行分析,不僅減少了計算過程縮短了計算時間,并且形象化的展現出凹坑結構的應力分布,使我們可以更好的了解凹坑結構的應力狀況。
1.1 凹坑缺陷的表征
由于大多數凹坑表面是不規則的,可以根據凹坑缺陷形狀按其外接矩形可將其規則化為長軸長度、短軸長度及深度分別為2X、2Y及Z的半橢球形凹坑。其中長軸 2X為凹坑邊緣任意兩點之間的最大垂直距離,短軸 2Y為平行于長軸且與凹坑邊緣相切的兩條直線間的距離,深度Z取凹坑的最大深度[3]。凹坑缺陷的表征示意圖見圖1。
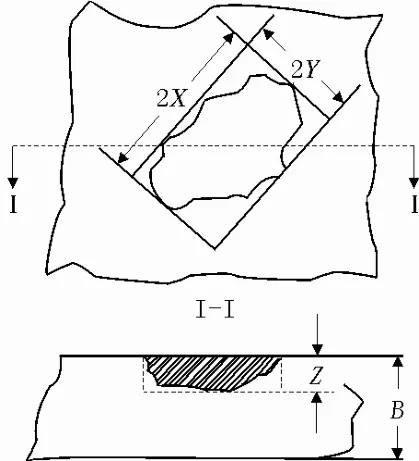
圖1 凹坑缺陷的表征示意圖Fig.1 Schematic characterization of pit defect
1.2 建立模型
擬定模型參數為表1所示[4]。利用有限元ANSYS軟件對尺寸為長短軸為20 mm,深度為4 mm的淺球型凹坑進行模擬分析,采用SOLID95實體單元,由于結構的對稱性可以取四分之一筒體進行分析,劃分網格如圖2所示。
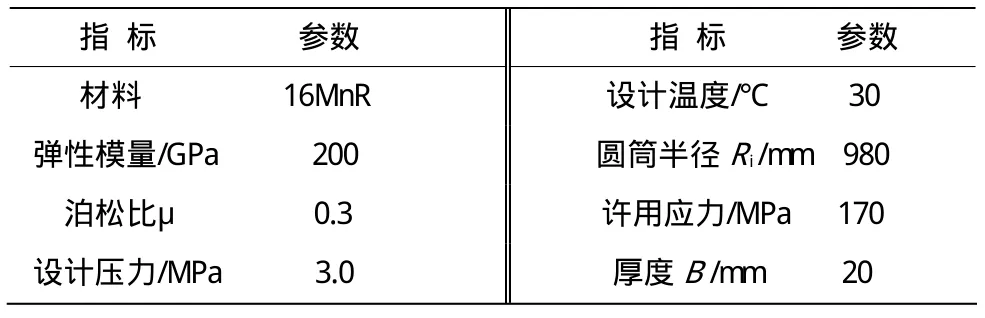
表1 模型參數Table 1 Model parameters
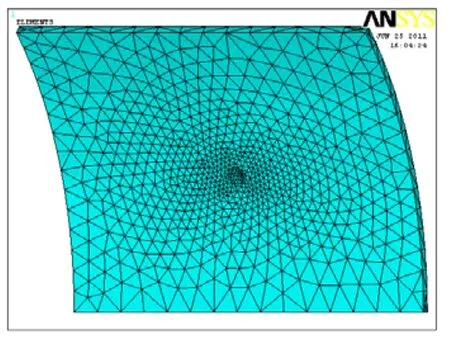
圖2 單凹坑的網格模型圖Fig.2 The finite element calculation model of single pit
1.3 施加載荷及求解應力分布
壓力容器內表面承受的設計應力p=3.0 MPa,對稱面施加對稱約束,通過軟件計算,其應力分布圖如圖3所示。最大應力σmax=205.2 MPa位于凹坑坑底處,最小應力σmin=71.4 MPa位于沿環向方向的凹坑邊緣處。
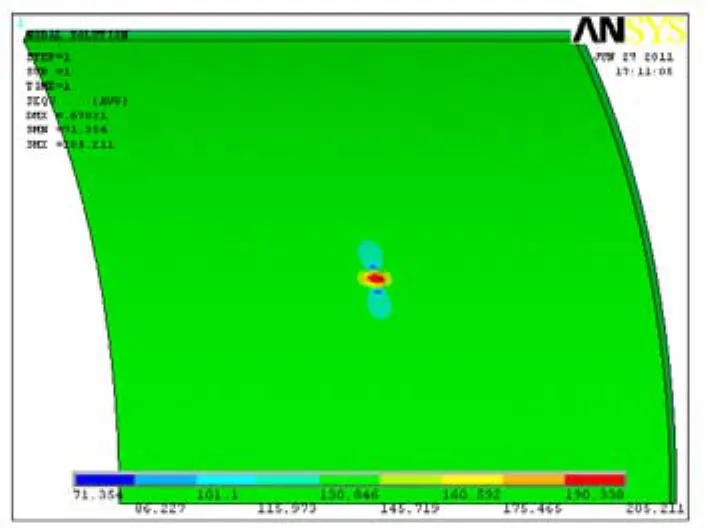
圖3 單凹坑的Mises應力分布Fig. 3 Mises stress of single pit
2 雙凹坑的應力分布及干涉效應
在石化設備中,由于多數凹坑是由腐蝕產生的,所以常常在容器局部形成密集的凹坑群。因此研究凹坑群的應力分布及應力集中的干涉效應,具有重要實際意義[5]。 本文主要分析環向和軸向排列的雙凹坑不同間距分布時應力分布及應力集中系數的影響。模型選取與上述單個凹坑相同,分別對兩凹坑間中心距離為0,10,20,30,40,50,60,80,100 mm的雙凹坑進行靜力分析。
2.1 雙凹坑應力分析
利用有限元ANSYS軟件對含有環向排列和軸向排列雙凹坑的壓力容器分別進行模擬靜力分析,通過計算可知這2種排列方式對應力分布的干涉效應影響是不同的,其應力云圖見圖4,5。
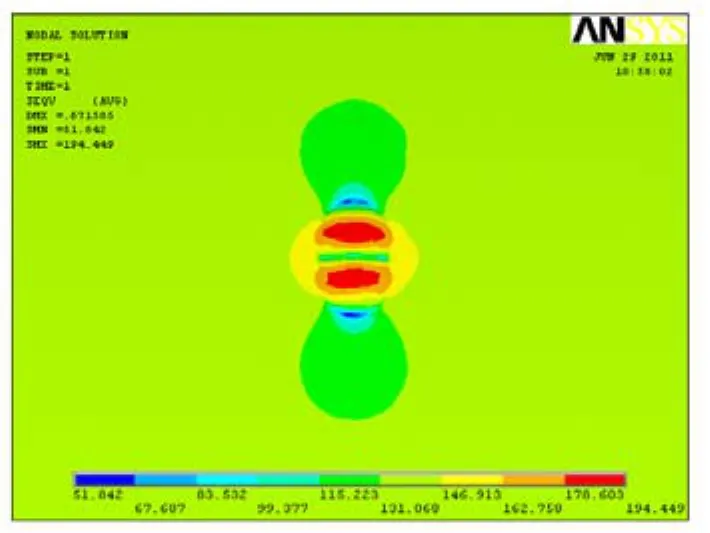
圖4 環向排列雙凹坑相交時的應力分布Fig.4 Stress cloud when ring direction two pits cross
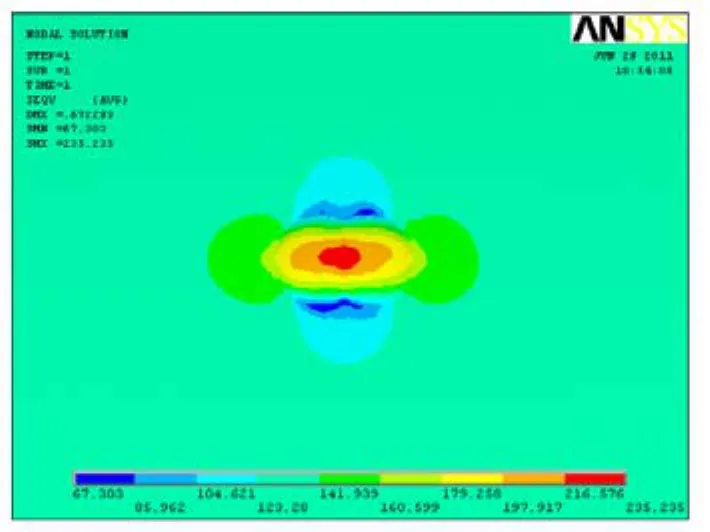
圖5 軸向排列雙凹坑相交時的應力分布Fig.5 Stress cloud when axial direction double pits cross
由雙凹坑應力云圖4、5,可以形象的展現出環向排列的雙凹坑相交時,最大應力位于各自坑底處,且最大應力值小于單個凹坑的最大值;軸向排列的雙凹坑相交時,最大應力位于相交中心處,最大應力大于單個凹坑的最大應力。
凹坑的存在會在壓力容器表面產生局部結構不連續,從而產生應力集中現象,對壓力容器安全極為不利,根據《應力集中系數》[6]可知:
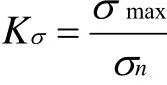
式中:Kσ—應力集中系數;
σmax—最大正應力,MPa ;
σn—名義正應力,MPa 。
其中σn=134.7 MPa為壓力容器無凹坑缺陷時的最大正應力,通過計算得出沿環向和軸向排列的雙凹坑最大主應力和應力集中系數,為了便于研究把結果列入表2、3 中。
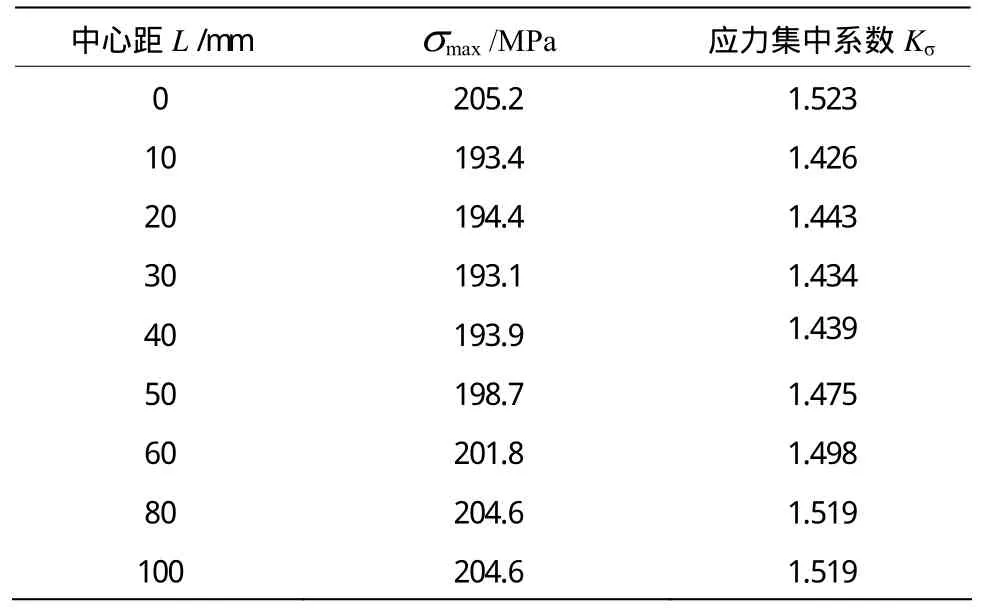
表2 環向分布的雙凹坑最大應力和應力集中系數Table 2 The maximum principal stress and stress concentration coefficient when double pits arrange along the ring direction
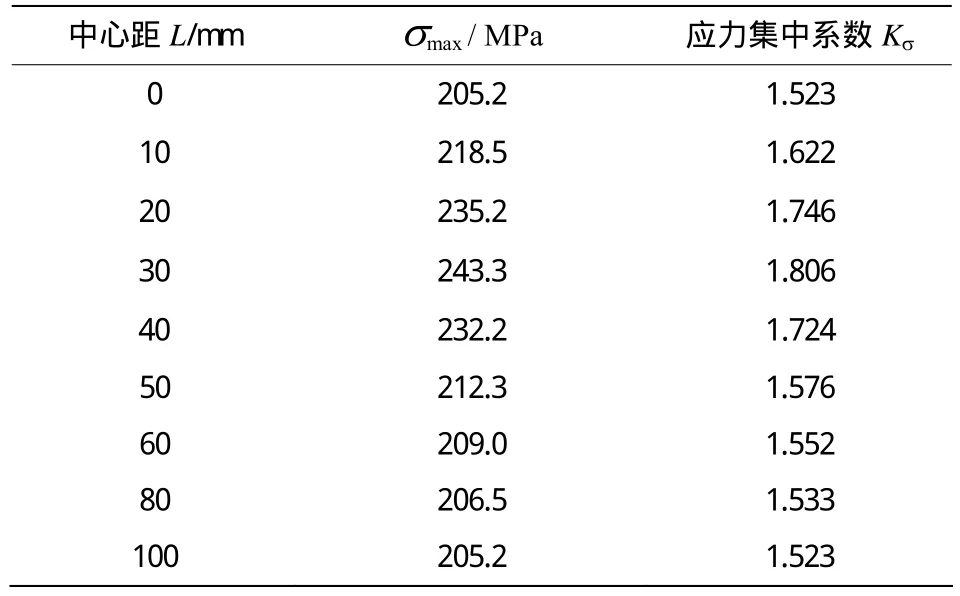
表3 軸向分布的雙凹坑最大應力和應力集中系數Table 3 The maximum principal stress and stress concentration coefficient when double pits arrange along the axial direction
2.2 數據分析
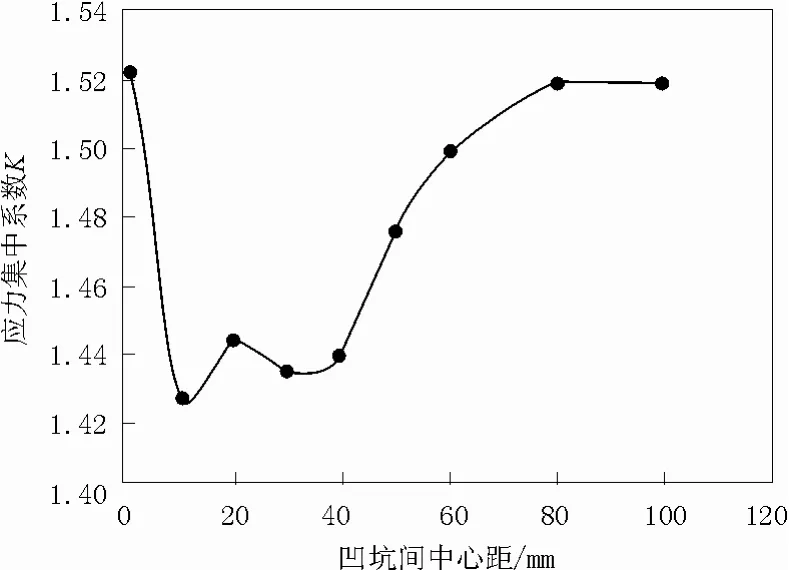
圖6 雙凹坑環向排列應力集中系數隨凹坑間距離變化曲線Fig.6 Double-pit in ring stress concentration coefficients change curve with distance between the pits
根據表2、3的數據,可繪出沿環向和軸向排列的雙凹坑應力集中系數隨凹坑間距離的變化曲線,如圖6、7所示。響不同。環向排列的雙凹坑,應力集中系數隨兩凹坑相對距離先減小后增加。軸向排列的雙凹坑,應力集中系數隨兩凹坑相對距離先增加后減小。
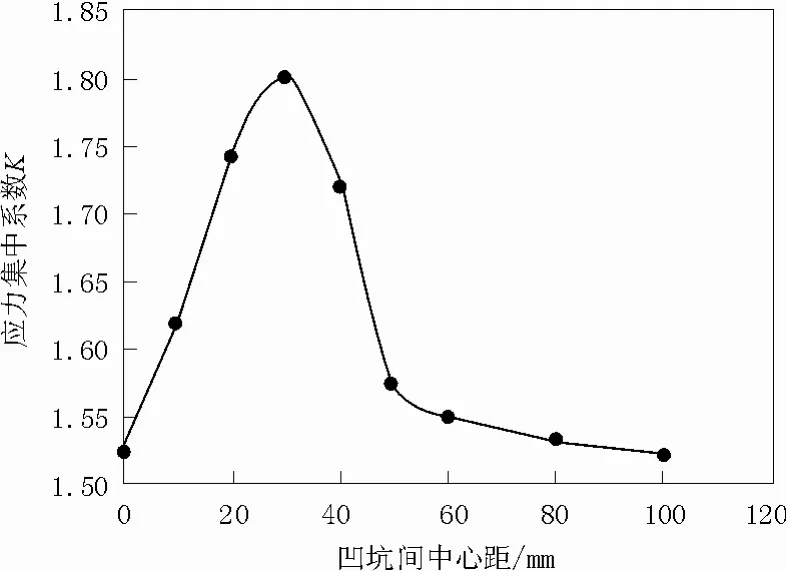
圖7 雙凹坑軸向排列應力集中系數隨凹坑間距離變化曲線Fig.7 Double-pit in axial stress concentration coefficient change curve with distance between the pits
對于環向排列和軸向排列的雙凹坑,當兩凹坑的中心距≥80 mm時,雙凹坑的最大應力值近似于單個凹坑的最大應力,這符合GB/T 19624-2004.《在用缺陷壓力容器安全評定》中當相鄰兩凹坑邊緣間最小距離大于較小凹坑的長軸 2X時,則可將兩個凹坑視為互相獨立的單個凹坑分別進行評定[3]。
3 結 論
由于壓力容器表面凹坑的存在會在壓力容器表面產生局部結構不連續,從而產生應力集中現象,嚴重的影響了壓力容器的安全運行。通過有限元ANSYS軟件對含有雙凹坑的壓力容器進行靜力分析計算,可知并不是所有凹坑排列方式對于壓力容器都有害。沿環向排列的雙凹坑,當兩凹坑相交時應力集中系數小于單個凹坑應力集中系數,對于安全有利。軸向排列的雙凹坑,當兩凹坑相交時應力集中系數大于單凹坑應力集中系數。因此壓力容器中含有軸向排列的雙凹坑更加危險,檢修時要重點關注。
[1] 趙菊 ,王茂廷. 壓力容器多凹坑干涉效應分析[J]. 化工機械,2010,36(6):579-581.
[2] 余偉煒,高柄軍.ANSYS在機械與化工裝備中的應用[M].北京:中國水利水電出版社,2006.
[3] 國家技術監督局.GB/T 19624-2004在用缺陷壓力容器安全評定[S].北京:中國標準出版社,1998.
[4] 國家技術監督局.GB150-1998鋼制壓力容器[S].北京:中國標準出版社,1998.
[5] 王炯華,楊鐵成.淺球形雙凹坑或多凹坑對應力集中的增強效應[J].實驗力學,1994,9(3):270-271.
[6] 彼德森RE.應力集中系數[M]. 楊樂民,葉道益,譯.北京:國防工業出版社,1988.
Analysis of the Doubt-Pit Interferential Effect of Pressure Vessels by ANSYS Software
GAO Yu,WANG Mao-ting,LIN Guo-qing,HAI Jun
(College of Mechanical Engineering, Liaoning Shihua University, Liaoning Fushun 113001, China)
Some problems that pits decreased strength of pressure vessels were analyzed and studied. The maximum stress was calculated by the finite element analysis software ANSYS, and double pits interferential effect was analyzed.The results show that, the double pits arrange along the ring direction, when two pits cross, the stress concentrating coefficient is less than a single pit stress value,so it is favorable to security of pressure vessels. But double pits arrange along the axial direction, when the two pits cross, the stress concentration coefficient is bigger than a single pit stress value. Therefore, axial double pits are more dangerous.
Pit; Pressure Vessel; Finite Element; Interferential Effect
TQ 051.3
A
1671-0460(2011)09-0975-03
2011-07-02
高 宇(1985-),男,遼寧大連人,碩士研究生,研究方向:壓力容器的疲勞與可靠性。 E-mail: ggg601111@163.com。

