模糊魯棒控制器在結晶過程中的應用

李 偉，劉朝英，李建增，邸樹綱

（1.軍械工程學院電氣工程系，河北石家莊 050003；2.河北科技大學理工學院，河北石家莊050018；3.河北省高速公路京秦管理處，河北秦皇島 066001）

結晶過程是化工及制藥行業的典型操作單元，它不僅是生產過程中的重要環節，也是影響產品產量和質量的關鍵環節，結晶過程中晶核形成、生長與結晶過程中的溫度、溫度變化率、液位、攪拌速度等有關［1］。然而結晶過程是一個具有時變性、不確定性并存在耦合的復雜過程，傳統的控制方法難以得到理想的控制效果，在對結晶工藝過程及控制要求具體分析的基礎上，筆者提出了基于T-S模糊模型的H∞魯棒控制算法應用于結晶過程，并利用MATLAB對系統進行了仿真。

1 結晶過程

1.1 結晶原理

固體有機物在溶劑中的溶解度與溫度有關，一般隨著溫度的升高而增大。將固體粗產品在適當的溶劑中加熱溶解，使之飽和，再將此溶液冷卻，由于溶解度下降，溶液變成過飽和而析出較純的產品，這就是結晶過程。用結晶法進行提純是基于產品和雜質有著不同的溶解度。

1.2 青霉素結晶過程

目前中國青霉素純化多采用間歇式共沸結晶的方法，該方法是提純物質的重要方法，對熱敏性的抗生素采用此方法結晶是提高產品質量的有效方法。青霉素鉀（鈉）鹽均采用此法。青霉素鹽共沸結晶工藝原理為青霉素鹽丁醇稀釋液蒸餾時形成丁醇-水二元共沸物，利用丁醇-水二組分在較寬的液相組成范圍內蒸餾溫度穩定，溶液沸點下降等特點，在共沸蒸餾過程中以補加丁醇的方法將水分帶走，使溶液逐步達到過飽和狀態而析出結晶。其工藝結晶過程如圖1所示。

圖1 青霉素結晶過程Fig.1 Penicillin crystallization process

2 青霉素結晶過程數學描述

由結晶過程工藝要求可知，結晶罐溫度θ及溫度變化率˙θ的控制需要通過調節蒸汽流量Q1實現，結晶罐液位H的控制需要通過調整丁醇補充量Q2來實現。但蒸汽流量Q1改變不僅改變結晶罐溫度θ及溫度變化率˙θ，同時，蒸汽流量Q1的增加，會導致結晶罐液位H降低。丁醇補充量Q2的增加，會導致結晶罐溫度θ減少，但這種影響較小，與其他參數相比可以忽略不計，因此可得數學描述如下：

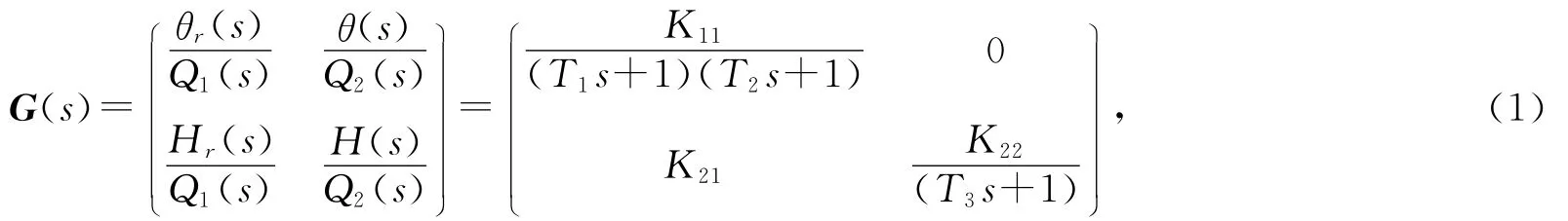
其中：K11為溫度變化對蒸汽流量的靜態增益；K21為液位對蒸汽流量的靜態增益；K22為液位對丁醇流量的靜態增益；T1，T2分別為蒸汽對夾套溫度的時間常數和夾套溫度對結晶罐內液體溫度的時間常數［2］。

結晶過程中，結晶罐溫度控制和液位控制間存在一定的耦合，而且K11，K21，K22及T2均隨結晶罐內液體成分的改變而改變；即該對象有一定的時變性，由此傳統控制難以得到良好的控制效果。

3 模糊魯棒控制器

筆者針對青霉素結晶過程機理復雜，系統具有非線性、時變性和較大的滯后性，難以建立被控對象精確數學模型的特點，建立系統的T-S模糊模型，設計狀態反饋H∞控制器，以LMI為優化工具，進行仿真研究。

3.1 T-S模糊模型

T-S模糊模型是一種本質非線性模型，易于表達復雜系統的動態特性，其主要思想是：每條模糊語句所表征的建模對象的局部動態特性用線性模型作為后件來表達，然后通過模糊隸屬函數將這些線性模型綜合起來構成全局模糊模型［4-10］。其典型的語言規則為

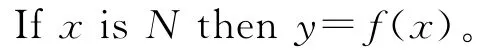
對于一個MIMO的非線性動態系統，如果T-S模糊模型后件采用狀態空間方程表示，則模糊規則可寫成

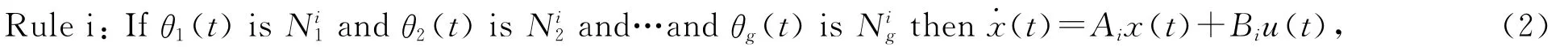
i為模糊規則數，Nij是模糊集合，θ（t）=［θ1（t），θ2（t），…，θg（t）］T是模糊規則的前件變量。

3.2 狀態反饋H∞控制

H∞魯棒控制理論是為具有模型攝動且MIMO系統提供的一種設計魯棒控制器的新方法，是在H∞空間通過某些性能指標的無窮范數解析優化而獲得的魯棒控制器，它可以很好地解決LQG理論不適于模型攝動情況及常規頻域理論不適于MIMO系統設計的情況。

對一個具體對象的數學模型來說，由于參數的不確定性與變化性，以及為了設計與計算的方便，就會簡化對象模型，因此造成對象模型存在一定的誤差。H∞魯棒控制的目的就是：當存在模型誤差時，如何利用對象模型來設計控制器，使得所設計的控制器在被控對象穩定的同時使某一目標函數T的H∞范數最小。

假設連續系統的被控對象G（s）的狀態方程描述為

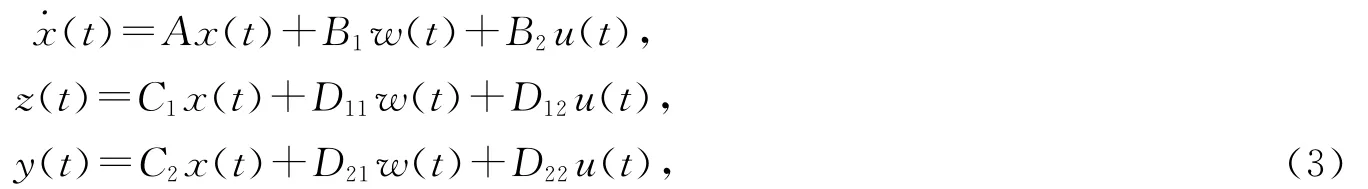
其中狀態x和干擾輸入w是可以直接測量的，則狀態反饋H∞控制就是要設計一個控制器

使得閉環系統：

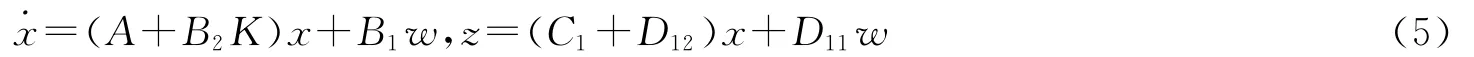
是漸近穩定的，且其閉環傳遞函數‖Tzw（s）‖∞的H∞范數滿足：

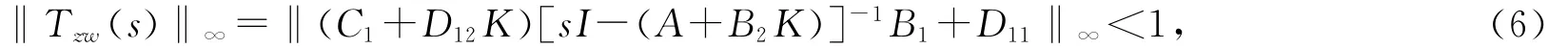
設計狀態反饋H∞的方法如下。

定理1 對系統（3）來說，存在一個狀態反饋H∞控制器，當且僅當存在一個對稱正定矩陣X和矩陣W時，使得如下的矩陣不等式

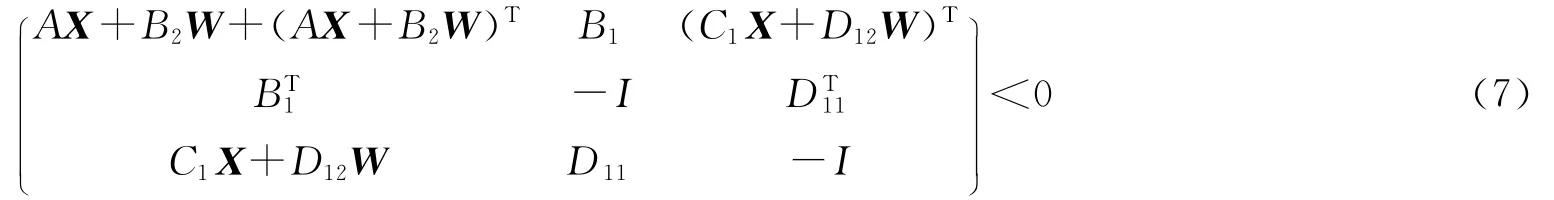
成立。進而，如果矩陣不等式（7）存在可行解X＊，W＊，則u=W＊（X＊）-1x是系統（4）的一個狀態反饋H∞控制器［11-18］。

3.3 狀態反饋H∞控制器的設計

根據結晶的工藝過程，建立T-S模糊模型，設計狀態反饋H∞控制器。其結構圖如圖2所示。

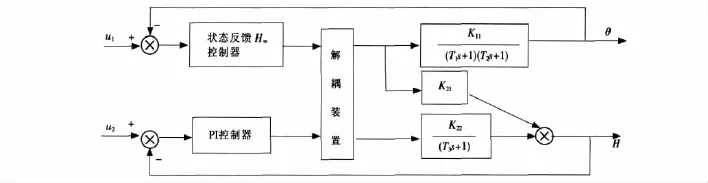
圖2 狀態反饋H∞控制器Fig.2 H∞state feedback controller

首先將結晶過程的數學模型轉化為狀態空間方程的形式，即：

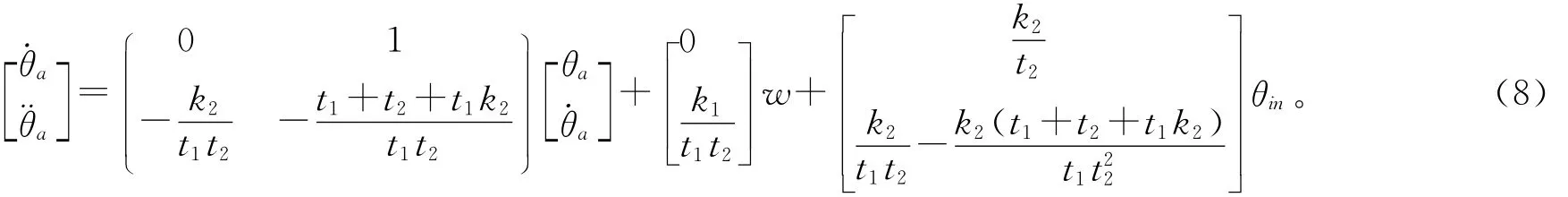
由結晶工藝過程可知在結晶過程中結晶罐內的溶液密度隨著溫度的變化而不斷變化，即丁醇和水分的含量是變化的。由相關書籍可知丁醇的沸點為35℃，因此研究對象溫度在20～40℃變化，根據結晶罐內丁醇和水分的含量隨著溫度的變化而不斷變化，選取溫度θa作為模糊模型的前件，建立青霉素結晶過程溫度的T-S模糊模型。設θa=x1=x2，則溫度系統的T-S模糊模型可作如下描述。

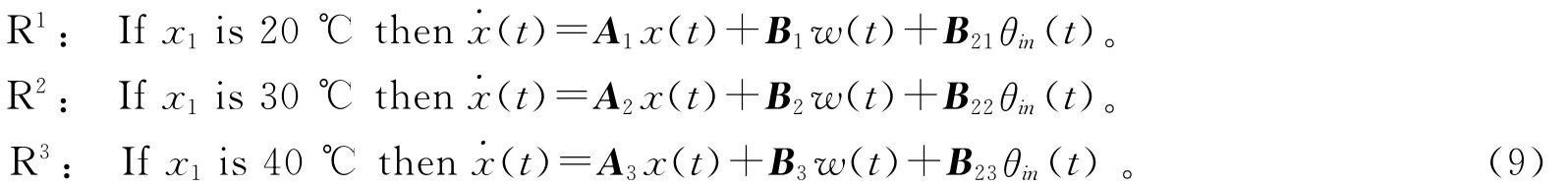
其中：

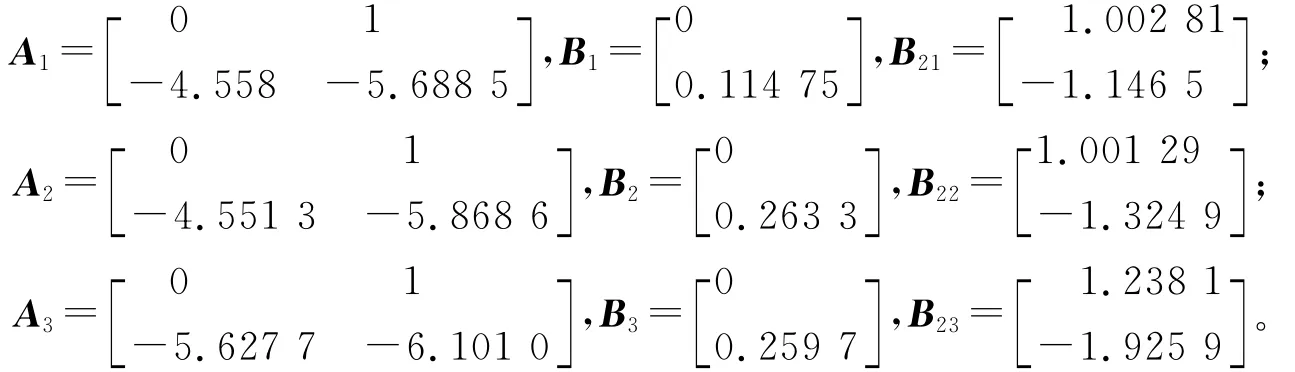
采用定理1對結晶過程的溫度系統（8）設計狀態反饋H∞控制器，利用MATLAB解矩陣不等式（7），得到使溫度系統漸近穩定，且滿足系統性能指標的狀態反饋矩陣為

4 仿真及分析

根據實際青霉素結晶的初始條件，對設計的控制器進行仿真，其結構圖如圖2所示，其中T1=13.2s，T2=189s，T3=53.1s，K11=0.18，K21=0.48，K22=1.01。

仿真結果如圖3—圖5所示。圖3為結晶過程溫度響應曲線，圖4為溫度系統的參數K2發生變化時仿真曲線，圖5為溫度系統的參數t2發生變化時的響應曲線，其中曲線1為狀態反饋H∞控制器作用下的溫度響應，曲線2為傳統PID控制器作用下的溫度響應。由圖3可看出，狀態反饋H∞控制器作用下的系統響應速度較快，調節時間較短，控制效果較好，而PID控制器作用下的系統響應速度較慢，調節時間較長并存在一定的超調。由圖4、圖5可看出，當溫度系統的參數K2，t2發生變化時，傳統PID控制器作用下的系統響應即曲線2因系統參數發生變化，響應速度變慢，調節時間變長并存在一定的振蕩現象，不能達到較好的控制效果。而狀態反饋H∞控制器作用下的系統響應即曲線1并沒有因為系統參數的變化出現振蕩現象，系統響應曲線仍然較平穩，控制效果較好。由此可以看出相對于傳統PID控制，狀態反饋H∞控制器作用下系統響應速度較快，調節時間較短，穩定性較高，即使在系統受到干擾的情況下仍可以具有較好的控制效果，更好的提高了系統的穩定性。

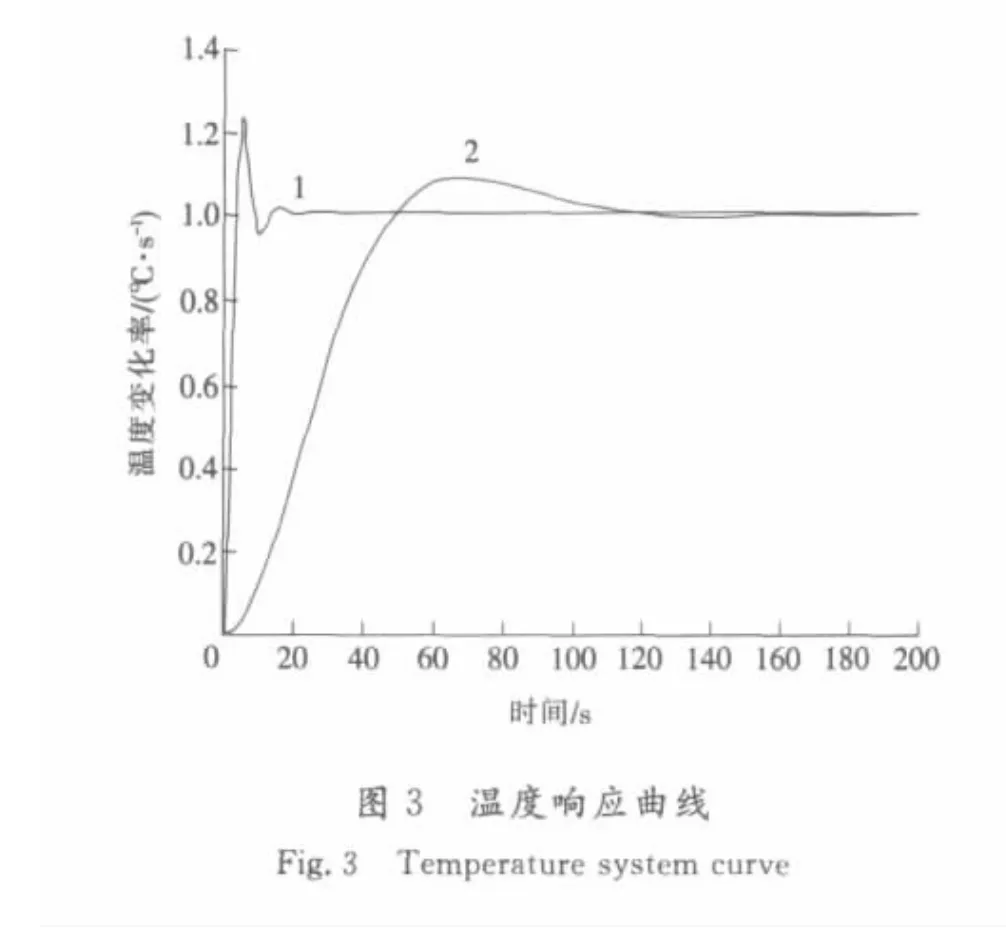
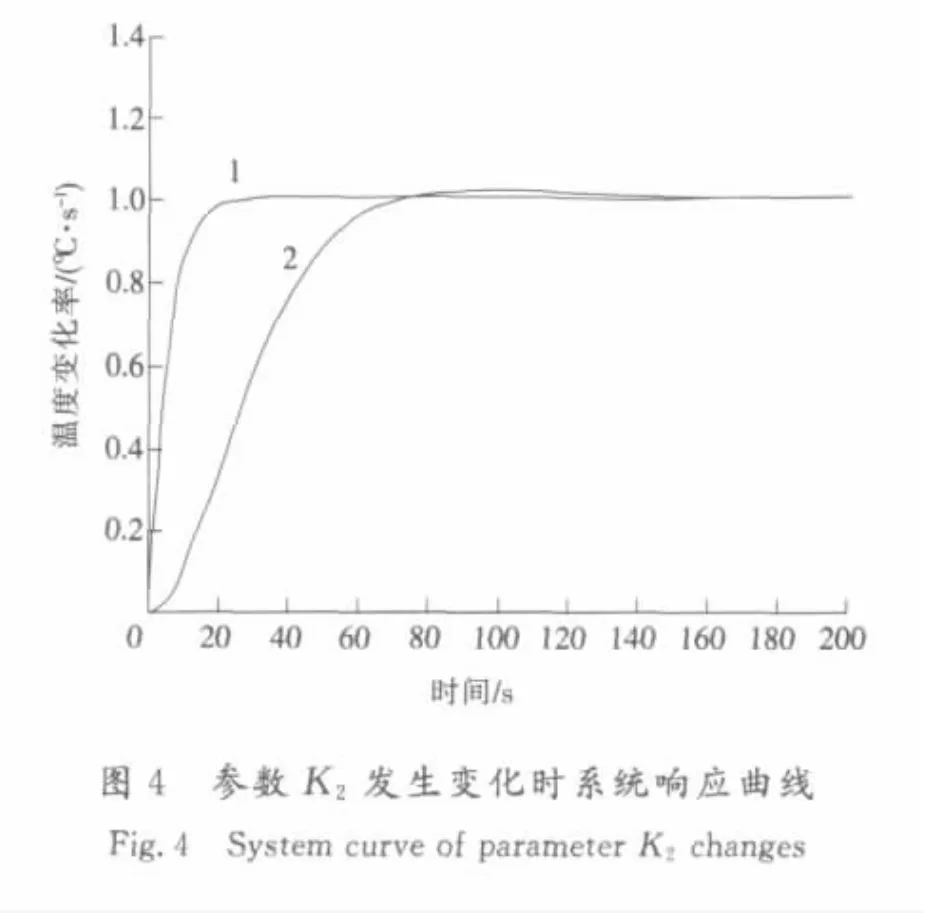
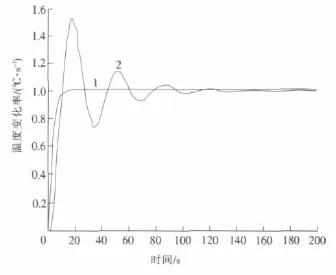
圖5 參數t2發生變化時系統響應曲線Fig.5 System curve of parameter t2changes

［1］ 葉鐵林.化工結晶過程原理及應用［M］.北京：北京工業大學出版社，2006.

［2］ 劉朝英，宋哲英，宋雪玲.模糊解耦控制在青霉素結晶過程中的應用［J］.河北工業大學學報（Journal of Hebei University of Technology），2005，34（8）：19-22.

［3］ 郭慶祝，孟維明，宋 揚，等.模糊控制技術發展現狀及研究熱點［J］.自動化博覽（Automation Panorama），2005，6（4）：68-70.

［4］ 劉曉東，張慶靈，王 巖.關于T-S模糊系統的穩定性［J］.東北大學學報（自然科學版）（Journal of Northeastern University（Natural Science）），2002，23（6）：531-534.

［5］ 黎 倩，劉朝英，宋哲英，等.模糊控制在循環流化床鍋爐床溫控制系統中的應用研究［J］.軍械工程學院學報（Journal of Ordnance Engineering College），2009，21（5）：72-75.

［6］ 徐小平，劉朝英.模糊解耦控制器設計及應用［J］.河北工業科技（Hebei Journal of Industrial Science and Technology），2008，25（5）：35-38.

［7］ 李盼盼.基于T-S模型的非線性系統模糊辨識方法研究［D］.南京：江蘇大學，2008.

［8］ 黎 倩.模糊魯棒控制在循環流化床鍋爐控制中的應用研究［D］.石家莊：河北科技大學，2010.

［9］ 王惠芳，劉朝英，宋雪玲，等.基于遺傳算法的模糊控制器參數優化［J］.河北科技大學學報（Journal of Hebei University of Science and Technology），2007，28（4）：276-278.

［10］ 羅秋濱，謝元貞.非線性系統的模糊建模方法研究［J］.哈爾濱理工大學學報（Journal of Harbin University of Science and Technology），2006，11（6）：16-18.

［11］ 褚 健，俞 立.魯棒控制理論及應用［M］.杭州：浙江大學出版社，2004.

［12］ 劉朝英，王惠芳，宋雪玲，等.一種改進的模糊調節神經網絡及其應用［J］.河北科技大學學報（Journal of Hebei University of Science and Technology），2008，29（4）：295-297.

［13］ TANAKA K，IKEDA T，WANG H O.Robust stabilization of a class of uncertain nonlinear systems via fuzzy control：Quadratic stability，control theory，and linear matrix inequalities［J］.IEEE Transactions on Fuzzy Systems，1996，4（1）：1-13.

［14］ 湯 偉，施頌椒，王孟效，等.魯棒控制理論中3種主要方法綜述（一）［J］.西北輕工業學院學報（Journal of Northwest Institute of Light Industry），2000，18（4）：54-59.

［15］ LIU Chao-ying，LI Wei，SONG Xue-ling.Application of robust regulator in crystallization process［J］.Proceedings-International Conference on Intelligent Computation Technology and Automation，2008，1（1）：1 004-1 007.

［16］ LIU Chao-ying，SONG Xue-ling，SONG Zhe-ying.Investigation on application of fuzzy decoupling control into penicillin crystallization process［J］.IEEE International Conference on Machine Learning and Cybernetics，2005，4（14）：762-766.

［17］ LIU Guo-cai，LIU Chao-ying.Study on the all-coefficient adaptive sequential decoupling control［J］.International Journal of Modelling，Identification and Control，2009，3（4）：180-185.

［18］ LO J C，LIN M L.Robustnonlinear control via fuzzy static output feed back［J］.IEEE Transactions on Circuits and Systems I：Fundamental Theory and Applications，2003，50（11）：1 494-1 502.