基于RSSI＆DFP的無線傳感器網絡聲源目標定位算法

劉立陽，張金成，吳中林，倪 鵬

(空軍工程大學導彈學院，陜西三原 713800)

無線傳感器網絡(Wireless Sensor Network，WSN)就是由部署在監測區域內大量的廉價微型傳感器節點組成，通過無線通信方式形成的一個多跳的自組織的網絡系統［1］。在無線傳感器網絡的眾多應用領域中，目標定位是其中的一個重要方面，它是利用網絡內多個傳感器節點檢測到的目標信息估計出某一時刻該目標的位置。而基于接收信號強度指示(Received Signal Strength Indicator，RSSI)的聲源目標的定位方法由于其不受視線影響、隱蔽性好、能耗小、易于實現等特點普遍存在于常見目標和檢測環境中。

聲源目標定位算法可分為兩類，一類以最大似然方法為基礎，得到以聲源位置和能量為參數的似然函數，然后通過搜索或者迭代的方式求出結果。另一類以最小二乘方法為基礎，將不同節點接收到的能量相比，消去聲源能量，然后用最小二乘的方法進行計算。通過對聲源定位算法進行分析不難發現，最大似然方法要比最小二乘方法的定位精度高很多，所以在對定位精度要求比較高的場合往往采用前一種方法。Zhao Feng等人［2－4］采用聲音幅值衰減模型，推導出似然函數的概率分布，借助序貫貝葉斯估計對目標進行定位;Sheng Xiaohong等人［5－6］基于聲音能量衰減模型，應用極大似然法對目標進行定位。在最大似然方法中，似然函數的建立直接決定了定位精度的好壞，同時在對似然函數進行求解時，算法的選取往往也對收斂速度的快慢產生重要的影響。為此，本文以傳感器節點在二維空間中自由分布為背景，以聲源能量衰減模型為基礎，用最大似然方法將聲源的定位問題轉化為似然函數的最優化問題，運用DFP(Davidon-Fletcher-Powell)算法解決搜索似然函數極值的問題，從仿真結果來看，這種算法相比于其它運用似然函數的算法而言，定位精度有明顯提高，并且能夠有效地提高算法迭代的收斂速度，符合對定位精度要求較高的實際應用的需要。

1 聲源能量的衰減模型

1.1 聲源能量衰減模型的推導

在推導聲音能量衰減模型之前需要做如下假設:(1)聲音在均勻介質中全向傳播;(2)不考慮傳感器網絡內障礙物的影響，并將目標源看作一個點聲源;(3)假設背景噪音是均值為0，方差已知的高斯白噪聲;(4)假設聲源衰減能量與背景噪聲能量互不相關。

由聲音的傳播規律可知，聲音信號的能量與它傳播距離的平方成反比［7－10］，聲源能量衰減模型正是利用這一特性，通過將每個聲音傳感器節點檢測到的聲音信號轉化為能量值，代入模型估計出聲源的位置。模型具體推導如下:

假設聲源目標某時刻t進入無線傳感器網絡的監測區域，此時有N個節點檢測到聲音信號，則傳感器節點i檢測到的能量可表示為:

其中，ei(t)表示t時刻傳感器節點i測得的聲音信號能量;si(t)表示t時刻聲源傳播到節點i衰減后的能量值;εi(t)表示t時刻節點i處的噪聲能量值。

si(t)又可以表示為:

其中，gi表示傳感器節點i處的噪聲影響系數;S(t)表示t時刻的聲源能量;ri表示節點i的位置坐標;r(t)表示t時刻聲源目標的位置坐標。節點和目標位置坐標均為二維坐標。

令di(t)=|r(t)－ri|，可以得到聲音能量衰減公式:

1.2 噪聲能量εi(t)均值和方差的推導

噪聲能量εi(t)概率密度的求取非常關鍵，它反映了測量節點受噪聲的影響程度，對于后續的目標定位算法有著重要的意義。假設在時間窗(t－T/2，t+T/2)內采樣點的個數為M，采樣頻率為fs，則可以得到窗長為T=M/fs，假設ai(t)為t時刻傳感器節點i處噪聲的幅值，服從高斯分布N(0，)，則

其中，εi(t)服從χ2分布，根據中心極限定理，當M足夠大時，εi(t)近似服從正態分布，并可以得到:

εi(t)的均值

εi(t)的方差

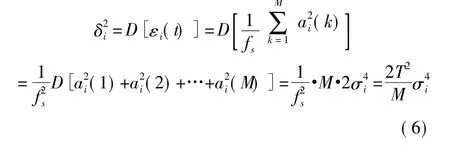
2 基于DFP的聲源定位算法

2.1 最大似然函數的求取

本文通過最大似然方法對聲源目標進行定位，首先需要完成對最大似然函數的求取，基于聲源能量的最大似然函數即未知量的先驗概率密度函數是根據節點處噪聲能量εi(t)的概率密度函數來獲得的。由于 εi(t)服從正態分布N(μi)，所以ei(t)的概率密度函數為:

由于每個傳感器節點處的噪聲能量互不相關，所以最大似然函數可以表示為:

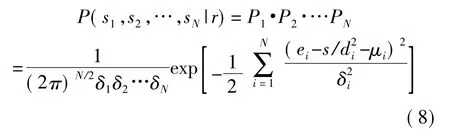
上式中節點接收的能量、噪聲能量均值和方差都為測得的量，未知量為信號能量s和聲源目標的位置坐標r，使似然函數最大的未知量的值即為待估計量的估計值。

2.2 DFP 算法

同時可以得到迭代公式:

在本文的聲源目標定位中，DFP算法的具體迭代步驟為:

(4)檢驗是否滿足收斂準則，若‖▽L(rk+1)‖≤η則停止迭代，得到點=rk+!;否則，進行步(5);

(5)若k=3則令r1=rk+!，返回步(2);否則進行步(6);

(6)令 gk+1=▽L(rk+1)，Δrk=rk+1－rk，Δgk=gk+1－gk。利用式(10)計算Hk+!置k=k+1，返回步(3)。

2.3 DFP算法運用中的幾個問題

2.3.1 未知聲源能量的估計

目標函數中有三個未知數x，y，s，由于進入無線傳感器網絡探測區域的目標的聲音能量是未知的，其范圍也是不定的，這給DFP算法的迭代帶來很多麻煩，似然函數的收斂性也變得十分復雜，所以需要對參數s進行估計處理，用范圍已知的x，y來表示聲源目標的能量s。由于傳感器節點處接收到的聲源能量ei在實際應用中是可以測到的，所以可以用聲音能量衰減公式對聲源能量進行估計，本文中對能源能量s的估計采用對每個傳感器節點估計值進行加權平均的方法確定，即0.05;

(2)置H1=I3(單位矩陣)，計算出在r1處的梯度g1=▽L(r1)，置k=1;

(3)令 dk=－Hkgk，從 rk出發，沿方向dk搜索，求步長λk，使它滿足

這種表示不僅有利于對目標函數的分析，更重要的是對求s關于x，y導數也十分方便，如果s關于x，y的表達式非常復雜的話，導數的表達式就難以表示出來，使得在DFP算法中s就必須作為一個參數參加迭代并且需要給出初始值，這樣就很難避免目標函數局部最小，而不能得到全局最優值。

2.3.2 迭代中收斂過慢的處理方法

由DFP算法的正定性和二次終止性可知，DFP算法的搜索方向為下降方向，即每次迭代使函數值有所下降，但在實際中由于計算節點數量有限以及噪聲的干擾，往往會出現收斂速度過慢的問題［11－13］，對于此種情況處理方法有兩種，一種是增加處理節點的數量，另一種是設定一個迭代的閾值。本文中，參與計算的節點是能夠探測到聲源能量的所有節點，所以前一種方法不適用于本文的討論，所以采用后一種方法進行算法的討論和仿真。

3 仿真實驗及結果分析

本文中傳感器節點的分布、聲源目標的設置、能量模型的建立、噪聲的加入、模擬數據源的建立以及算法的運算等都在MATLAB軟件中仿真實現。

假設無線傳感器網絡的探測區域為50 m×50 m的方形區域，傳感器節點的數量為10個，在探測區域中隨機分布(在軟件中用randn函數實現)，聲源坐標設為探測區域的中心，背景噪聲分布為N(0，1)。

3.1 目標函數L的仿真實現

仿真中，x∈(－25 m，25 m)，y∈(－25 m，25 m)，聲源實際位置為(0，0)，由于目標函數在不同點的值差距很大，所以為了顯示方便，顯示了目標函數以e為底的對數的值。可以證明該函數的對數形式和函數的單調性是一致的，完全可以由函數對數的單調性來判斷函數的單調性。圖1、圖2為目標函數示意圖。

圖1 目標函數側視圖

圖2 目標函數俯視圖

由似然函數的物理意義可知，圖中最大值所在的位置為傳感器節點的位置，它們的坐標是已知的，函數只有一個全局最小值，它所在的位置即為待估的目標聲源的位置。

3.2 DFP算法的仿真實現

本次仿真目標聲源位置坐標的初始迭代點設為x0=(1 1)，經過計算得到目標聲源的最終位置坐標為x=(0.048 4 －0.056 5)，迭代次數為50次，耗時為0.161 841 s。其中傳感器節點與聲源目標的分布如圖3所示，x，y在迭代中的變化如圖4所示。

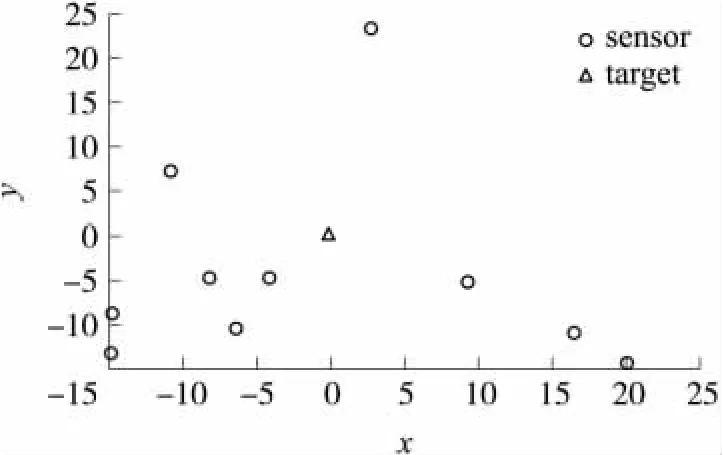
圖3 傳感器節點與目標分布圖

圖4 DFP方法在迭代過程中x，y收斂情況

由上圖可以看到，在迭代10次以后x，y就比較平穩不再有大的起伏，向更高的精度逼近，而且收斂速度也比較快，只迭代了50次就搜索到了全局最優解，而在相同條件下分布式EM算法［14］需要更多的迭代次數，精度也比DFP算法下降十倍左右，所以說DFP方法是非常優秀的一種解決無線傳感器網絡聲源目標定位的方法。

4 結論

本文基于聲音能量衰減模型和最優化理論中的DFP算法研究了傳感器節點隨機分布條件下的無線傳感器網絡聲源目標定位問題。仿真實驗結果表明，文中提出的算法能夠滿足對目標定位精度和速度要求較高的場合，具有一定的實際應用意義。但此種算法是建立在集中式的處理方式之上的，這種處理方式會使整個網絡擔負較高的能耗，這一問題可以用分布式的思想加以解決，這也是下一步需要進行深入研究的問題。

［1］孫利民，李建中，陳渝，等.無線傳感器網絡［M］.北京:清華大學出版社，2005.

［2］Chu M，Haussecker H，Zhao F.Scalable Information Driven Sensor Querying and Routing for ad hoc Heterogeneous Sensor Networks［J］.International Journal of High Performance Computing Applications，2002，16(3):293－313.

［3］Zhao Feng，Shin Jaewon，Reich J.Information Driven Dynamic Sensor Collaboration for Tracking Application［J］.IEEE Signal Processing Magazine，2002，19(2):61－72.

［4］Liu J，Reich J，Zhao F.Collaborative In Network Processing for Target Tracking［J］.EURASIP Journal on App lied Signal Processing，2003，2003(1):378－391.

［5］Sheng X H，Hu Y H.Energy Based Acoustic Source Localization［C］//Proceedings of The 2nd International Workshop on Informa2tion Processing in Sensor Networks(IPSN’03)，2003.

［6］Xiaohong S，Yuhen H.Maximum Likelihood Multiple Source Localization Using Acoustic Energy Measurements with Wireless Sensor Networks［J］.IEEE Transactions on Signal Processing，2005，53(1):44－53.

［7］Li D，Hu Y U.Energy Based Collaborative Source Localization Using Acoustic Micro Sensor Array［J］.EUROSIP Applied Signal Process，2003，5:321－337.

［8］胡仕萍，李思敏，唐智靈.基于WSN的聲源目標定位算法研究［J］.兵工自動化，2008，27(7):63－65.

［9］趙昭，陳小惠.無線傳感器網絡中基于RSSI差值的改進定位算法［J］.廈門大學學報(自然科學版)，2008，47(3):361－364.

［10］林瑋，陳傳峰.基于RSSI的無線傳感器網絡三角形質心定位算法［J］.現代電子技術，2009，2:180－182.

［11］李兆斌，魏占禎，徐風麟.無線傳感器網絡增強的質心定位算法及性能分析［J］.傳感技術學報，2009，22(04):563－566.

［12］魏雅川，梁 彥，陳延軍，等.無線傳感器網絡自適應聲音目標定位算法［J］.傳感技術學報，2010，23(03):418－422.

［13］林金朝，李國軍，周曉娜，等.基于動態能量管理的無線傳感網絡動目標定位跟蹤方法［J］.通信學報，2010，31(12):90－96.

［14］賈子熙，吳成東，張云洲，等.無線傳感器網絡中一種分布式聲源定位方法［J］.系統仿真學報，2009，21(20):6552－6555.