基于經驗模態分解的光纖陀螺隨機序列平穩化處理*

張秋昭，張書畢* ，侯東陽，劉萬利

(1.中國礦業大學國土環境與災害監測國家測繪局重點實驗室，江蘇徐州 221116;2.中國礦業大學環境與測繪學院，江蘇 徐州 221116)

在慣性技術中，常把慣性測量單元(Inertial Measurement Unit，IMU)誤差分為系統性誤差和隨機性誤差，其中系統性誤差可以通過測試和標定進行補償;而隨機性誤差隨時間變化，成為影響IMU精度的關鍵因素。常用的隨機誤差辨識方法主要包括功率譜密度(PSD)［1］、Allan 方差［2－3］、時間序列法［5－7］和自相關函數估計［6］法。

譜密度刻畫了一個平穩時間序列的功率譜，并特征化其二階矩的性質。通過研究估計后的譜密度，可以識別引起數據最大變化的頻率范圍，因此可以用信號的功率譜密度來表征信號的頻域特性，可以應用于辨識慣性傳感器的隨機誤差［1，7］。Allan方差是20世紀60年代提出的一種方法，最初被用于研究高精度振蕩器的頻率穩定性，后來用于辨識慣性傳感器隨機誤差，由于其可以辨識出較多的誤差項，得到了大家的廣泛重視［2－3］。自相關函數法由于其辨識能力和精度有限［6］，應用不多。

PSD和Allan方差法都需要用近似擬合曲線得到隨機模型，但這些估計是兩次統計建模，含有較大統計誤差［8］，而時間序列分析方法(AR模型等)只需做一次統計分析，建模精度高，并可以得到等效的連續狀態方程表達式，常用來作為激光陀螺等高精度慣導系統的建模方法［4］。但AR模型常要求序列為穩態隨機過程，而中低精度的光纖陀螺(Fiber Optic Gyro，FOG)常含有趨勢項或周期性誤差，必須對隨機序列進行去平穩化處理［8］。

目前常見的平穩化處理的主要方法［9］:多項式回歸、小波分析等。多項式回歸由于原理簡單易于實現，在平穩化處理中得到了廣泛應用。常見的多項式擬合多假設序列含有現行趨勢項或二次項，多項式的階數如何取，取的的階數太少，擬合精度不高，太高會產生過擬合現象［9］;小波分析可以提取序列的趨勢項［10］，但小波基、閾值、分解的層數的選擇受主觀性影響比較嚴重。

經驗模態分解方法(Empirical Mode Decomposition，EMD)是一種自適應的局部時頻分析方法［11］，它根據信號自身的特性將信號自適應地分解成有限個經驗模態函數，特別適合非平穩信號分析，在信號去噪、趨勢項剔除等方面得到了廣泛應用［11－12］。黨淑雯等引入基于經驗模態分解的提升小波消噪技術，去除光纖陀螺中的1/fγ類型分形噪聲［13］。曲從善等采用一種基于經驗模態分解的濾波方法對激光陀螺隨機信號進行消噪［14］。論文引入經驗模態分解，以低精度光纖陀螺KVH-CPT為實驗對象，對陀螺輸出的序列進行平穩化處理，采用逆序法驗證平穩化效果，與小波分析等方法的對比實驗結果表明，EMD方法能有效提前陀螺隨機序列的趨勢項，實現陀螺序列的平穩化處理。

1 AR模型

描述隨機序列{xt}某一時刻t和前p個時刻序列值之間的相互關系表示為

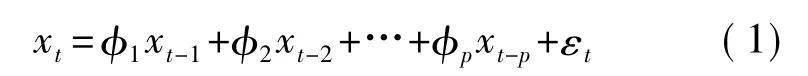
若隨機系列{εt}是白噪聲且和前一時刻序列xk(k＜t)不相關，則這樣的模型稱為p階自回歸模型，記為AR(p)。

AR(p)模型描述的是這樣的一種平穩隨機過程:該隨機過程在t時刻的觀測值xt與t時刻之前的觀測 εt－1，εt－2，…εt－p存在相關性，即與過去p個時刻的觀測值存在相關性。因此，AR模型常用來描述陀螺的隨機噪聲［7，9］。

2 平穩化檢驗

AR模型描述的是隨機平穩序列的方法，因此在用AR對隨機系列進行建模時必須首先對隨行序列進行平穩性檢驗。

平穩性檢驗的主要目的是檢驗陀螺隨機誤差時間系列是否具有不隨時間原點的推移而變化的統計特性。如果隨機誤差系列是平穩的，再假設序列服從正態分布，則對陀螺隨機誤差的研究，就可以采用單個樣本的時間序列代替總體平均，這就給數據處理帶來很大方便。如果不平穩，則需要對數據進行平穩后處理［8－9］。

造成隨機序列不平穩的主要原因是其中包含有隨時間緩慢變化的趨勢項。檢驗這種非平穩趨勢項的一個很有效的方法是逆序法［9］，簡述如下:

(1)對于測試數據x1，x2，…，xn，將其分為M小段，然后求各小段的平均值，得到一個大致不相關的均值序列y1，y2，…，yM。

(2)對于下標為i的yi，每當出現yj＞yi(j＞i，i=1，2，…，M－1)時就將其定義為yi的一個逆序，與yi對應的逆序的個數Ai稱為yi的逆序數。

(3)記序列y1，y2，…，yM的逆序總數定義為:

(4)記隨機整數序列A的均值和方差分別為:

如果λ值處于±2之內，則可接受序列無趨勢的假設(在0.05顯著水平上);否則拒絕該假設，認為序列為非平穩序列［9］。

3 經驗模態分解原理

經驗模態分解將信號分解為滿足以下條件的模態函數(Intrinsic Mode Function，IMF):零點數目相同與極值點數目相同或至多相差1;函數關于局部平均對稱;最終將信號表示成若干IMF與單調殘差函數之和:

其中，imfi(t)表示i個IMF，rn(t)是單調殘差函數。EMD算法采用所謂的“篩”完成，其基本步驟為:

①求取信號x(t)的極值點;

②分別由極小值點與極大值點求得包絡線emin(t)和emax(t);

③計算上下包絡的平均值m(t)=(emax(t)+emin(t))/2;

④提取細節d(t)=x(t)－m(t);

⑤對細節d(t)重復進行①至④步驟，直至d(t)為一個零均值，此時d(t)即為一個IMF;

⑥計算殘差r(t)=x(t)－imfi(t);

⑦重復運算直至殘差不含有IMF。

應用EMD進行多尺度信號分解時，定義如下按尺度標準化模量的累積均值［12］(Mean of the Accumulated Standardized Modes，MASM):

其中m≤nimfi(t)是第i尺度的模量。如果明顯偏離零均值，則認為從尺度m開始是信號的趨勢變化所致。去趨勢項后的信號可以表示為:

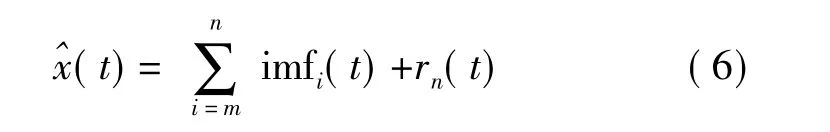
4 實驗分析

為了驗證論文的方法，以KVH－CPT型號開環光纖陀螺為實驗對象。靜態采集了該光纖陀螺的原始觀測值，處理后得到實測陀螺隨機信號序列，如圖1所示。對其采用逆序法進行平穩性檢驗，求得統計參數 λ=－5.2613，由前所述 λ?［－2，2］，拒絕假設，認為該序列為非平穩序列。采用EMD提取趨勢項，結果如圖2所示，當分層至13層時，其累積均值明顯偏離0值，如圖3所示。可以認為剩余的信號為趨勢項見圖2(b)。對去除趨勢項重構后的序列采用逆序法求取統計量 λ=0.4935，λ∈［－2，2］，則接受檢驗，認為該序列為平穩序列。

圖1 陀螺信號去偏后的序列

圖2 數據一EMD分解圖及分解尺度與累加均值的關系

采用偏態系數和峰態系數對其進行正態性檢驗。偏態系數(Skew Value)ξ和峰態系數(Kurtosis Value)υ的定義為:

其中μxσx分別為序列xt的均值和中誤差。偏態系數ξ和峰態系數υ的理想取值為0和3［9］。

同時采用Matlab中函數庫中的去趨勢項函數dtrend和小波分析方法對該序列進行處理。經過多次實驗，發現當小波分析采用‘db4’小波基和分解層數為20層時效果較好。比較得到的結果如表1所示。

采用EMD對隨機序列處理前后結果的數值比較見表1。

表1 數據一幾種方法處理前后結果比較

為了使論文采用的方法更具說服力，采用上述方法對另一種數據進行同樣的處理，結果如圖3和表2所示。其中小波分析方法中采用‘db4’小波基，分解層數為18層。

圖3 數據二EMD分解圖及分解尺度與累加均值的關系

表2 數據二幾種方法處理前后結果比較

由表1和表2可以看出，dtrend函數對隨機序列的趨勢項提取效果較差，小波分析方法和EMD方法，均能分辨出原始隨機序列的趨勢項，均能明顯改善原隨機序列的平穩性，正態性也略有改善。但小波分析方法需要多次實驗才能確定最佳的小波基和分解層數，而EMD方法能自動判斷分解層數，效果較好。

5 結論

AR模型等時間序列分析方法常用來對光纖陀螺隨機誤差建模，但其只能對平穩序列進行建模和處理。論文以低精度光纖陀螺為實驗對象，采用經驗模態分解對非平穩信號序列進行平穩化處理，并與小波分析等方法進行了比較實驗。結果表明:該方法能有效辨識非平穩信號序列中的趨勢項，平穩化后的信號可以采用時間序列分析方法進行建模。

［1］Yi Yudan.On Improving the Accuracy and Reliability of GPS/INSBased DirectSensorGeoreferencing.［D］.TheOhioState University Ph.D Dissertation.2007.

［2］Naser El-Sheimy，Hou Haiying，Niu Xiaoji.Analysis and Modeling of Inertial Sensors Using Allan Variance［J］.IEEE Transactions on Instrumentation and Measurement，2008，57(1).:140－149.

［3］熊凱，雷擁軍，曾海波.基于Allan方差法的光纖陀螺建模與仿真［J］.空間控制技術與應用，2010，36(3):7－13.

［4］Tang Jianghe，Fu Zhenxian，Deng Zhenglong.Indntification Method for RLG Random Errors Based on Allan Variance and Equivalent Theorem［J］.Chinese Journal of Aeronautics.2009，(22):273－278.

［5］方靖，尚捷，顧啟泰.光纖陀螺隨機誤差建模的實驗研究［J］.傳感技術學報，2008，21(9):1514－1518.

［6］Nassar 2003 Modeling Inertial Sensor Errors Using Autorgressive Models［C］//Proceedings of the Institute of Navigation(ION)National Technical Meeting(NTM 2003)，2003:116－225.

［7］吳富梅.GNSS/INS組合導航誤差補償與自適應濾波理論的拓展［D］.解放軍信息工程大學博士論文.2010.

［8］朱奎寶，張春熹，張小躍.光纖陀螺隨機漂移ARMA模型研究［J］.宇航學報，2006，27(5):1118－1121.

［9］馮慶奇.激光陀螺捷聯慣性導航系統組合導航及零速修正技術研究［D］.國防科學技術大學碩士論文.2009.

［10］周哲，莊良杰，熊正南，等.基于小波分析的陀螺漂移趨勢項提取［J］.中國慣性技術學報，1999，7(4):58－61.

［11］Huang N E，Shen Z，Long S R.The Empirical Mode Decomposition and the Hilbert Spectrum for Nonlinear and Non-Stationary Time Series［J］.Proceedings of the Royal Society A，1998，(454):903－995.

［12］王堅，高井祥，王金玲.基于經驗模態分解的GPS基線解算模型［J］.測繪學報，2008，37(1):10－14.

［13］曲從善，于鴻，許化龍，等.基于經驗模態分解的激光陀螺隨機信號消噪［J］.紅外與激光工程，2009，38(5):859－863.

［14］黨淑雯，田蔚風，金志華.基于經驗模態分解的光纖陀螺1/fγ類型分形噪聲濾除方法［J］.紅外，2009，30(10):12－17.