一種基于Graph Cuts的多尺度乳腺腫塊分割方法*

吳相穎，徐偉棟，厲力華*，劉 偉，張 娟，邵國良，Zheng Bin

（1.杭州電子科技大學生命信息與儀器工程學院，杭州 310018; 2.浙江省腫瘤醫院放射科，杭州 310022; 3.匹茲堡大學放射學系，賓夕法尼亞州 15213，美國）

乳腺癌是當今女性最常見的惡性腫瘤之一。乳腺X線攝影是目前乳腺癌最常用和最有效的診斷手段之一［1－2］。然而，由于乳腺組織的復雜性及有限的分辨率等原因，乳腺X線圖像往往不夠清晰，加上人的視覺感知等主觀因素，臨床醫生在閱片時容易出現漏檢或診斷錯誤。為了幫助醫生更好地診斷病情，乳腺鉬靶計算機輔助診斷技術(Computer Aided Diagnosis，CAD)成為了目前國際上的研究熱點。

腫塊分割作為腫塊檢測和診斷的關鍵環節，是CAD的一個研究熱點，許多學者做了大量的工作［3－6］。然而由于乳腺圖像中噪聲、偽影較多，腫塊形狀和背景復雜多變，現有方法的分割結果往往不夠理想。

基于Graph Cuts理論［7］的圖像分割技術最早來源于組合優化理論。該算法基本過程為:首先分別選定部分圖像像素作為目標和背景，然后以像素作為節點，以像素之間的相鄰關系作為邊，構造一個圖(Graph)，最后運用最大流/最小割算法對網絡進行切割，得到的最小割對應于待分割的目標邊界。Graph Cuts算法具有全局最優求解能力及結合多種知識的統一圖像分割框架，引起了研究者越來越多的關注，在乳腺腫塊分割方面也有所應用［8－9］。但是，海量的節點及為達到一定分割精度而采用的迭代求解模式，使得大多數基于Graph Cuts的分割算法耗時較大。當臨床醫生手動選定的目標和背景像素較少時，在目標和背景的邊界容易出現一些像素被錯誤劃分情況。另外，大量交互操作加重了臨床醫生工作量，降低了分割速度，不適合進行批量圖像分割處理。

Rother等人［10］對交互式 Graph Cuts算法進行改進，提出了GrabCut算法。它進一步簡化了交互操作，用戶只需要選定一個矩形框包含整個目標，將框外的像素作為背景，利用Graph Cuts進行多次迭代，得到對象和背景的分割結果。然而由于乳腺組織和病灶的復雜性，乳腺圖像中乳房組織和病灶區域的灰度通常是不均勻的，這使得傳統Graph Cuts算法以及GrabCut算法在分割乳腺腫塊圖像時結果往往并不理想。

針對乳腺圖像的這些特點，本文提出一種基于Graph Cuts算法的多尺度乳腺腫塊自動分割方法。首先，采用區域統計融合方法對圖像進行粗分割，將得到的粗輪廓替代傳統Graph Cuts算法中的手動標記，并作為后續Graph Cuts分割的初始輪廓。在迭代優化階段，本文引入多尺度分析方法，以高斯金字塔分解得到的多尺度圖像序列代替固定尺度的原始圖像序列估計GMM參數，將粗糙尺度的易分割性與精細尺度的精確性互補，使得算法快速確定GMM參數以執行Graph Cuts分割。考慮到傳統Graph Cuts算法處理海量的節點耗時較大，通過分水嶺變換將圖像劃分成若干內部連通且有良好邊緣的小區域塊，將區域塊內像素灰度的均值作為塊內每個像素的灰度強度以提高算法的抗噪能力，從而以較少的分塊替代海量的像素進行分割。

本文第2部分介紹基于Graph Cuts算法的多尺度圖像分割方法，第3部分對提出的方法進行實驗驗證，并與交互式Graph Cuts算法和GrabCut算法進行了實驗對比，最后給出本文的結論。

1 方法

1.1 傳統交互式Graph Cuts算法

圖像分割問題是一個將像素標為目標/背景的典型二元標號組合優化問題。Graph Cuts理論的核心思想在于構造一個能量函數，然后運用組合優化技術最小化該能量函數。通過構造網絡、最小化能量函數及網絡流理論，可以把標號問題轉換為用最大流/最小割方法［11］來解決。

設G=(V，E)為一無向圖，在邊集X上定義容量函數c:E→R+，稱圖G及其邊集E上的容量函數c構成了一個s－t網絡，記作N=(G，s，t，c)，其中，s和t分別稱為網絡的源點和匯點。定義t-link為圖G中連接節點與s或t的邊。通過最小化Gibbs能量函數E(f)，把頂點集V劃分為分別與源點s和匯點t相連的兩個頂點集S，T(s∈S，t∈T)。

式中:f為V的一個標號，f:P→L(L∈{“obj”，“bkg”})。R(f)只與像素的灰度有關，稱為數據能量項;B(f)只跟鄰域標號相關，稱為平滑能量項。系數λ≥0，指定了數據能量項與平滑能量項的相對重要性。

圖1是我們使用傳統交互式Graph Cuts算法對一幅乳腺圖像ROI分割的結果。圖1(a)為手動標記操作。其中，腫塊內部標記代表目標種子點，腫塊外部標記代表背景種子點。圖1(b)為傳統Graph Cuts分割結果。式(1)中的數據能量項R(f)和平滑能量項B(f)分別通過下面公式計算:

圖1 傳統交互式Graph Cuts算法的分割結果

如圖1(b)所示，無論是腫塊內部還是周圍區域，灰度分布都不均勻，Graph Cuts算法雖然可以大致地分割出腫塊輪廓，但對腫塊邊緣細節分割并不理想，如圖1(b)腫塊的邊緣區域A并沒有得到很好分割。

1.2 基于Graph Cuts的多尺度乳腺腫塊自動分割方法

針對乳腺圖像分割問題，無論是腫塊內部還是周圍區域，灰度分布都不均勻，Graph Cuts算法雖然可以大致地分割出腫塊輪廓，但對腫塊邊緣細節分割并不理想。另外，大量交互操作加重了臨床醫生工作量，不適合進行批量圖像分割處理。因此，本文提出一種基于Graph Cuts算法的多尺度乳腺腫塊自動分割方法。

本文提出的方法概述如圖2所示。首先，應用統計區域融合方法對乳腺圖像進行粗分割，并將獲得的粗輪廓替代手動標記的“目標”和“背景”種子點。通過實驗測定平滑參數σ的初值，并將σ按照公式 σ=α·σ(0＜α＜1)更新。迭代 Graph Cuts算法進行分割，對每一次 Graph Cuts分割結果，通過GMM建立目標類和背景類的灰度分布模型，然后利用目標類和背景類的距離變換更新先驗概率。結合先驗概率和GMMs計算后驗概率，并將其值賦予下一次Graph Cuts處理中的t-link。為了提高算法的分割速度，采用分水嶺算法將圖像劃分成若干內部連通且有良好邊緣的小區域塊，并以較少的分塊替代海量的像素進行Graph Cuts分割。通過多次實驗經驗可知，σ和α分別設置為2和0.6，迭代的次數為4次左右時就能取得較滿意的結果。

圖2 本文提出的方法概圖

1.2.1 區域統計融合

區域統計融合［12］(Statistical Region Merging，SRM)是一種線性時間快速、簡單的區域增長圖像分割算法。它基于自適應統計閾值，在灰度通道上合并而不需要保持動態區域鄰接圖的謂詞。該算法分兩步:①點對排序，將圖像按照四鄰接兩兩結合結成點對，選擇一個函數計算點對的融合代價，并按照融合代價的大小進行排序;②按照下式對排序結果進行圖像融合:

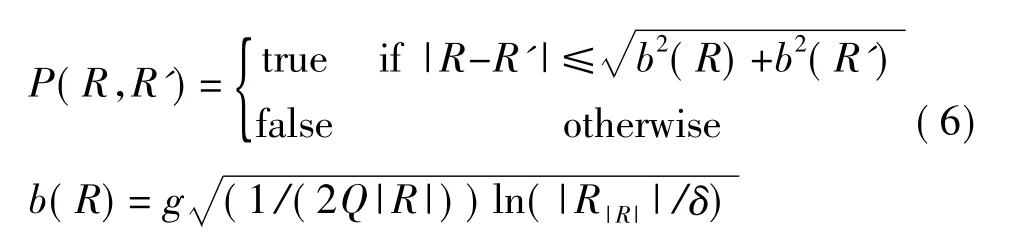
式中:R為區域中像素個數，b(R)為融合參數，δ為圖像總像素個數倒數的1/6，Q是質量因子，Q越大分割越細致。從實驗的角度來看，調整Q的值修改事件的統計復雜性，然后構建由粗到細(多尺度)分割圖像的層次結構，從而有可能控制分割的粗糙度。

通過SRM算法的處理，可以將圖像中紋理相同的像素融合為一個區域，完成對乳腺圖像的粗分割。同時提取分割結果的輪廓，替代傳統Graph Cuts算法中的手動標記，并作為后續Graph Cuts分割的初始輪廓。如圖3所示是一幅乳腺圖像SRM粗分割結果，圖3(b)為SRM分割結果。不同的色塊代表不同的區域，其中的灰度是取自色塊所在區域的原始圖像像素的灰度均值。圖3(c)為我們提取的粗分割圖像，并為后續分割提供初始輪廓。

圖3 SRM分割結果

1.2.2 高斯金字塔模型

考慮到乳腺圖像的灰度非均勻性和Graph Cuts算法本身局限性，我們引入多尺度分析［13］提高腫塊分割精度。

高斯金字塔［14］是一種經典的多分辨率空間圖像分析方法。定義I為原始圖像，G(σ)為高斯核函數。則平滑圖像L(σ)由下式給出:

注意到，如果高斯參數σ很大，我們需要增大窗口的尺寸來適應高斯濾波器，這在實際設計中存在很大困難，因此我們采用下采樣處理來獲取平滑圖像。特征為圖像尺寸隨著尺度水平的增加呈指數下降，粗尺度圖像是細尺度圖像的子集，不同尺度間圖像的像素在位置上仍保持著相應的幾何拓撲關系。

塔式分解n－1次后所得由粗至細的多尺度圖像序列為f(n－1)，f(n－2)，…，f(1)，以該圖像序列代替固定尺度的原始圖像序列來迭代分割獲取目標/背景樣本點。由于GMM參數估計是一個由粗至細、逐步求精的逼近過程，雖然最初的圖像尺寸較粗，對應的樣本容量較小，但并不影響對GMM參數的粗略估計，隨著迭代估計的進行，樣本容量也隨之增大，滿足了對GMM參數進一步準確估計的要求。塔式分解把精細尺度的精確性與粗糙尺度的易分割性兩者有機地統一起來，從而使得GMM參數估計過程更為快速有效。我們通過使用不同標準差值對原始圖像進行高斯濾波，之后迭代Graph Cuts算法，實現從全局到局部的逐步分割過程。

1.2.3 分水嶺變換

注意到傳統Graph Cuts算法是通過建立像素級的馬爾可夫隨機場(MRF)模型［15］實現分割，對于較大尺寸的乳腺腫塊圖像而言，海量的節點使得Graph Cuts處理耗時較大。因此本文采用分水嶺算法作為預處理將圖像劃分成若干個內部連通且具有良好邊緣的小區域塊，然后將區域塊內像素灰度均值作為塊內每個像素的灰度強度以提高算法的抗噪能力。在執行Graph Cuts階段，用區域塊替代像素作為新的節點進行分割，提高算法的運行效率［16］。

圖4所示為經過分水嶺算法分割產生的一個鄰域結構，每個節點代表一個區域塊，節點之間有邊相連接表示這兩個節點互為鄰域。圖4(a)是分水嶺過分割得到的6個區域塊，圖4(b)的鄰域結構是通過將擁有共同邊界的區域塊設為鄰域而建立的，這種鄰域結構在乳腺腫塊圖像分割的實驗中被證明有效。

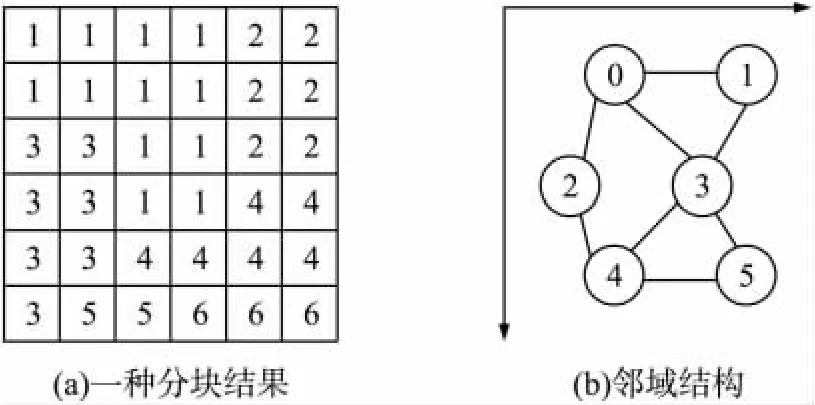
圖4 分水嶺分割產生的分塊結果及對應的鄰域結構

1.2.4 迭代優化與參數估計

根據前一次Graph Cuts分割結果的距離變換和灰度直方圖的可能性，計算先驗概率，并按照下面兩式將其值賦予下一次Graph Cuts處理中的t-link:

其中，Pr(O|Ip)和Pr(B|Ip)由下面公式給出:

Pr(Ip|O)，Pr(Ip|B)和 Pr(O)，Pr(B)由前一次Graph Cuts分割結果計算得到。圖5所示為根據可能性和先驗概率更新t-link。

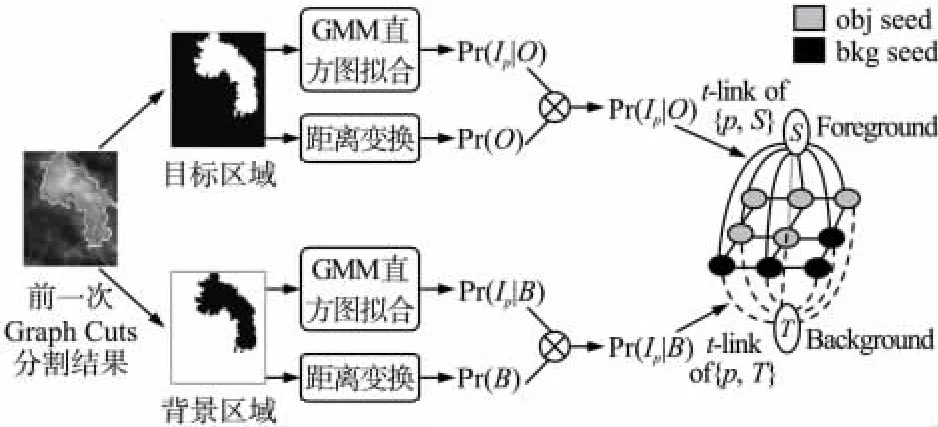
圖5 更新可能性和先驗概率

可能性Pr(Ip|O)，Pr(Ip|B)由GMM計算得到。GMM由下式獲得:

根據前一次Graph Cuts處理結果的空間信息更新先驗概率Pr(O)，Pr(B)。由于邊界附近像素點的下一次分割標號不確定，使用距離變換的結果更新先驗概率。節點到邊界的距離被歸一化到0.5～1范圍內。令dobj、dbkg分別為目標點和背景點的距離變換。則先驗概率為:

最后，利用GMM得到的Pr(Ip|O)，Pr(Ip|B)，和距離變換得到的Pr(O)，Pr(B)，根據式(8)和式(9)計算后驗概率。通過前一次Graph Cuts分割結果，我們獲取灰度直方圖的可能性和距離變換，并計算先驗概率，然后將其值賦予下一次Graph Cuts處理中的t-link。

2 實驗結果及討論

2.1 數據集

將本文方法應用于110例包含腫塊的乳腺X線圖像ROI(Region of Interest)進行腫塊分割實驗，以驗證算法的有效性和優越性。這些圖像來自于南佛羅里達大學的DDSM(Digital Dataset for Screening Mammography)數據庫，ROI圖像灰度均為8位，圖像尺寸平均值為709像素×708像素。

2.2 評價方案

為了比較分割方法的性能，我們將本文所提出的多尺度Graph Cuts算法與傳統的交互式Graph Cuts算法以及GrabCut算法做了實驗對比。

本文方法的參數設置:區域統計融合中質量因子Q的值指定為1，2，4，…，256 范圍內，Gibbs能量函數的系數λ設為0.5，高斯平滑參數σ和控制因子α分別設置為2和0.6，迭代的次數為4次。

為定量評價分割的質量，通常的做法是將算法分割得到的結果與該領域專家手動分割的結果進行像素級別的比較。為此，我們邀請了3位乳腺癌診斷研究人員對測試圖片進行手動分割，分割的結果作為實驗的比較輪廓。本文采用誤分率作為實驗結果的評價算法，誤分率定義為過分割率和欠分割率之和。其中，過分割率和欠分割率的定義如下:

誤分率的值越小，表示分割結果越好。當值為0時，表示算法分割結果與手工分割結果一致。

2.3 實驗與討論

將本文方法、交互式Graph Cuts算法以及Grab-Cut算法應用于110例腫塊病灶圖像，進行分割實驗，并對比最終的分割結果。

圖6為本文方法與交互式Graph Cuts、GrabCut分割結果的對比。第1列是交互式Graph Cuts的手動標記，其中腫塊內部標記代表目標種子點，腫塊外部標記代表背景種子點。第2列是相應的分割結果。從圖中可以看出，腫塊中心的灰度高于腫塊邊緣，而背景區域也因存在乳腺組織而呈現灰度非均勻性，Graph Cuts分割腫塊邊緣部分的結果并不理想。另外，交互式Graph Cuts分割需要大量的手動標記操作，因此加重了臨床醫生的工作量，而且不適合批處理分割。

圖6中第3列是GrabCut算法分割的結果。它進一步簡化了交互操作，用戶只需要選定一個矩形框包含整個目標，將框外的像素作為背景，利用Graph Cuts進行多次迭代，得到乳腺腫塊區域的分割結果。但是當初始標記與目標輪廓偏差較大時，該方法容易產生錯誤的分割結果，如該列的第2個和第3個分割結果。

圖6 本文方法與交互式Graph Cuts、GrabCut分割結果的對比

圖6第4列是本文方法的分割結果。通過結合SRM的粗分割和Graph Cuts的精分割，我們的方法實現了乳腺腫塊的自動分割。另外，分水嶺算法和多尺度分析提高了整體運行效率和分割精度。以圖6的第4行為例，左側圖片是交互式Graph Cuts的分割結果，可以看出，當腫塊內部灰度分布不均勻時，交互式Graph Cuts算法和GrabCut算法沒能準確地分割出腫塊邊緣，而我們的方法通過對已經比較接近真實輪廓的粗分割結果進行全局優化處理，得到了比較理想的分割結果。

左邊第1列為交互式Graph Cuts手動標記操作，第2列為交互式Graph Cuts分割結果，第3列為GrabCut分割結果，最后一列為本文方法分割結果。

表1列出了本文方法和傳統方法［7，10］分割結果的誤分率(%)。本文方法相比傳統交互式Graph Cuts算法獲得1.89%更好的分割結果。為了進一步說明3種分割方法之間的差異，根據傳統交互式Graph Cuts分割結果，我們定義誤分率低于2%的圖像為成功分割的圖像，誤分率超過2%的圖像為誤分割圖像。

表1 交互式Graph Cuts、GrabCut和本文方法分割結果的誤分率平均值 單位：%

表2列出了成功分割的圖像和誤分割圖像的誤分率(%)。在成功分割圖像的誤分率方面，本文方法和交互式Graph Cuts方法具有一定的可比性，如圖6的第1行和第2行分割結果。但是，在誤分割圖像方面，本文方法比交互式Graph Cuts方法擁有更好的分割結果，如圖6的第3行和第4行分割結果。交互式Graph Cuts算法分割得到的誤分割圖像的誤分率(0.77%)與成功分割圖像的誤分率(7.21%)相比差異較大，而本文方法通過引入多尺度思想，把Graph Cuts算法及GMM模型結合起來，利用圖像的全局和局部信息對腫塊進行分割，使得二者差異并不明顯，因此本文提出的方法具有較高的穩定性。實驗結果表明本文的方法在腫塊分割方面要優于交互式Graph Cuts算法和GrabCut算法。

表2 交互式Graph Cuts、GrabCut和本文方法成功分割的圖像以及誤分割圖像的誤分率平均值 單位：%

3 結論

本文提出一種基于Graph Cuts的多尺度腫塊自動分割方法。首先，應用區域統計融合方法對圖像進行粗分割，將得到的粗輪廓作為后續Graph Cuts分割的初始輪廓。在迭代優化階段，利用高斯金字塔分解得到多尺度圖像序列，將粗糙尺度的易分割性與精細尺度的精確性互補，從而以較少樣本快速確定GMM參數，以執行Graph Cuts分割。通過結合Graph Cuts算法和多尺度高斯平滑處理，本文提出的方法彌補了交互式Graph Cuts和GrabCut算法在處理腫塊邊緣細節以及交互處理方面的不足。另外，分水嶺算法對圖像進行預處理，提高了算法的分割速度及抗噪能力。本文的多尺度分割模型是通過Graph Cuts算法實現的，具有良好的全局最優求解能力，能夠較好地處理形狀復雜多變的乳腺腫塊分割問題。理論分析與實驗結果表明，本文的方法在乳腺腫塊分割方面具有良好的效果。

［1］Denise Guliato，Rangayyan R M，Carnielli W A.Segmentation of Breast Tumors in Mammograms by Fuzzy Region Growing［J］.IEEE Engineering in Medicine and Biology Society，1998，20(2):10022－10051.

［2］Cai Xiaopeng，Chen Xiaowei，Hu Liming，et al.Computer-Aided Detection and Classification of Mieroealeifieations in Mammograms:A Survey［J］.Pattern Recognition，2003，36(12):2967－2991.

［3］Chang Y H，Hardesty L A，Harim C M，et al.Knowledge-Based Computer-Aided Detection of Masses on Digitized Mammograms:A Preliminary Assessment［J］.Med.Phys，2001，28(4):455－461.

［4］Sheila Timp，Nico Karssemeijer.A New 2D Segmentation Method Based on Dynamic Programming Applied to Computer Aided Detection in Mammography［J］.Med.Phys，2004，31(5):958－971.

［5］Camilus K S，Govindan V K，Sathidevi P S［J］.Computer-Aided I-dentification of the Pectoral Muscle in Digitized Mammograms［J］.Journal of digital imaging，2009:1－19.

［6］Zou Fengmei，Zheng Yufeng，Zhou Zhengdong，et al.Gradient Vector Flow Field and Mass Region Extraction in Digital Mammograms［C］//21st IEEE International Symposium on Computer-Based Medical Systems，pp.41－43，2008.

［7］Boykov Y，Jolly M P.Interactive Graph Cuts for Optimal Boundary＆ RegionSegmentationofObjectsin N-D Images［C］//Proceedings of the 8th International Conference on Computer Vision，Vancouver，Canada，1:105－112，2001.

［8］Saidin N，Ngah U K，Sakim H A M，et al.Density Based Breast Segmentation for Mammograms Using Graph Cut Techniques［C］//TENCON(IEEE Region 10 Conf.)，2009，pp.1－5，doi:10.1109/TENCON.2009.5396042.

［9］Nafiza Saidin，Umi Kalthum Ngah，Harsa Amylia Mat Sakim，et al.Density Based Breast Segmentation for Mammograms Using Graph Cut and Seed Based Region Growing Techniques［C］//Second International Conference on Computer Research and Development，pp.246－250，2010.

［10］RotherC，Kolmogorov V，BLAKE A.GrabCut:Interactive Foreground Extraction Using Iterated Graph Cuts［C］//Proceeding of the 2004 SIGGRAPH Conference，Aug 2004，I;309－314.

［11］Boykov Y，Kolmogorov V.An Experimental Comparison of Min-Cut/Max-Flow Algorithms for Energy Minimization in Vision［C］//IEEE Transactions on Pattern Analysis and Machine Intelligence(PAMI)，September，2004.

［12］Richard Nock，Frank Nielsen.Statistical Region Merging［J］.IEEE Trans.Pattern Anal.Mach.Intell.，2004，26(11):1452－1458.

［13］Xu Ying，Hong Zhi.Study of Multi-Scale Enhancement Algorithm for THz Images Combining Wavelet Denoising［J］.Chinese Journal of Sensors and Actuators，2011，24(3):398－401.

［14］WANG Xun，ZHA Yu-fei，BI Du-yan.Image Segmentation Based on Multi-Resolution Analysis and Watershed Algorithm［J］.Opto-Electronic Engineering，2007，34(6):72－76.

［15］Li Xin-wu.Multisource Image Fusion Method Using Markov Random Field Model and EM Algorithm［J］.Chinese Journal of Sensors and Actuators，2006，19(2):525－529.

［16］Stawiaski J，Decencière E，Bidault F.Interactive Live Tumor Segmentation Using Graph-Cuts and Watershed［C］//Workshop on 3D Segmentation in the Clinic:A Grand ChallengeⅡ.Liver Tumor Segmentation Challenge.MICCAI，New York，USA，(2008).