基于ANSYS的異步電動機電磁場分析

王水發，陳德為

(福州大學機械工程及自動化學院，福建 福州 350108)

1 引言

異步電動機作為一種典型的電能—機械能轉換裝置，具有結構簡單、制造成本低等優點，已廣泛應用于人們的日常生產生活中。但在電機的使用過程中，不可避免的出現了各種各樣的故障，嚴重影響了人們的生產生活。因此，對電機的各種運行狀況和故障進行分析，以便進行優化設計具有重要的實際意義。傳統的電機電磁設計和故障分析都基于經典的電機電路計算方法，即“路”的思想［1］。雖然這種方法計算簡單，但由于電機空間的復雜性，它不能考慮電機材料的磁飽和、定轉子齒槽形狀和集膚效應等因素給電機帶來的影響。隨著計算機技術的高速發展，使將有限元“場”的方法引入到電機的分析中成為可能，它能精確的分析出電機的運行情況，以便進行故障診斷和優化設計。而ANSYS軟件是融結構、流體、電場、磁場、聲場分析于一體的大型通用有限元分析軟件。其電磁模塊和電路模塊能很好的對電機的電路和電磁場進行分析，具有很強的實現耦合功能，并且具有強大的后處理功能，能夠以圖表、曲線等形式顯示或輸出，以供我們分析處理，還有提供了功能強大的APDL語言，利用它可以簡單的實現某些GUI無法實現或實現起來很煩瑣的功能，避免重復工作。本文采用了電機經典的“路”思想和有限元“場”的思想相結合的方法，即場路耦合法［2－5］，利用ANSYS軟件對一臺異步電動機進行諧波仿真分析和偽靜止瞬態分析，分別用這兩種方法分析出電動機在空載與堵轉等運行狀況下的二維電磁場。

2 電磁場分析的基本原理

電磁場理論是由一套麥克斯韋方程組描述的，它的分析和研究也是基于麥克斯韋方程組。麥克斯韋方程組實際上是由安培環路定律、法拉第電磁感應定律、高斯定律和高斯磁通定律四個定律組成的，其微分形式如下所示［6］:

上述方程組中:H為磁場強度矢量;B為磁通密度矢量;E為電場強度矢量;D為電位移矢量;J為傳導電流密度矢量;ρ為自由電荷密度。

在電磁場問題中，以上四個方程存在以下的關系:

式中:ε為介電常數;μ為磁導率;σ為電導率。

3 電機場路模型的建立

3.1 電機等效電路模型的建立

本文采用的是場路耦合的方法，所以先把電機定子內的相繞組分為直線和端部兩部分進行考慮(如圖1所示)。端部用電阻和電感來等效代替，電阻表示端部本身的阻值，而電感用來模擬電機漏抗的影響。在進行諧波分析時，由于其只考慮基波的影響，故此時電感代表定子相繞組端部漏電感和諧波漏電感之和。而在進行偽靜止瞬態分析時，因為其已經考慮了諧波的影響，故此時電感只代表端部的漏電感。直線部分是以電流和矢量磁位為變量，用有限元的方法進行迭代計算，實現場路耦合。其相繞組場路耦合等效電路如圖2所示，因此電機定子相繞組電路的方程式為:

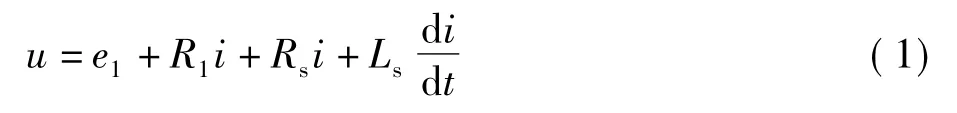
式中，u和i分別為電機定子相電壓和相電流;e1和R1分別為電機定子相繞組直線部分的感應電動勢和電阻;Rs定子相繞組端部電阻;諧波分析時，Ls為定子相繞組端部漏電感和諧波漏電感，偽靜止瞬態分析時，Ls只為定子相繞組端部漏電感。

圖1 電機定子相繞組的結構示意圖

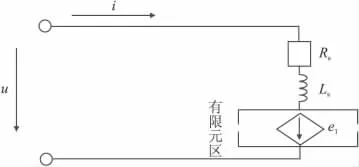
圖2 電機定子相繞組的場路耦合等效電路

因為本文分析的異步電動機轉子是鼠籠轉子，其等效電路可按照其空間位置進行連接，轉子導條、端環電阻和漏感組成的等效電路，滿足基爾霍夫定律，其等效電路模型如圖3所示。

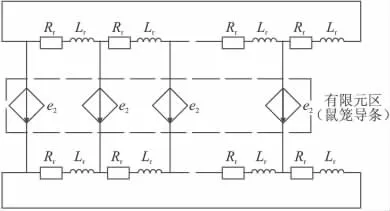
圖3 鼠籠轉子的場路耦合等效電路

3.2 電機二維場模型的建立

首先，在進行異步電動機二維有限元電磁場分析時，精度在工程允許的范圍內，需先對模型的邊界條件進行假設，以便簡化計算。本文模型分析做假設如下:

(1)忽略電機端部電磁場的影響，即電機沿軸向的每個橫截面的電磁場沒有變化。

(2)電機定子以外的空間不存在漏磁場。

(3)電機各部件材料各向同性。

(4)忽略位移電流。

基于以上的假設，電機的二維電磁場求解區域滿足渦流方程:

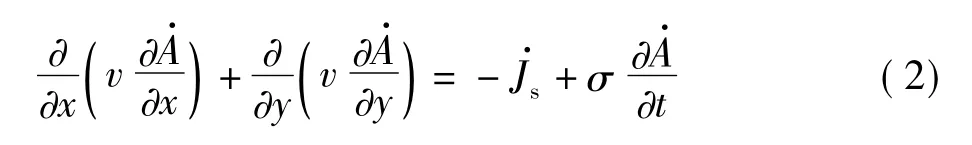
將電機的求解區域離散成很多網格單元，電機的網格劃分和整體的場路耦合模型分別如圖4、5所示。

因為電機定、轉子的感應電動勢e1、e2都是矢量磁位和定、轉子電流的函數，再根據電機的場邊界條件和路的邊界條件，即定子外圓的=0和三相相位相差120°的交流電電壓。以矢量磁位和電流為變量，離散求解區域，建立一個一組非線性方程組進行迭代求解，最后得出電機求解區域電磁場分布。

4 模型仿真與結果分析

本文仿真采用的是Y90L－4異步電動機，其基本參數如表1所示。

表1 Y90L-4異步電動機的基本參數

根據表1中的基本參數，在ANSYS軟件中建立電機的二維物理模型，選用PLANE53單元［7］作為單元分析類型(可以通過設置單元的實常數來改變定子繞組電流的方向)，并分別將每槽定子繞組和轉子導條所有節點的電流(CURR)和感應電動勢(EMF)自由度都進行耦合;選用CIRCU124單元［7］作為電路仿真單元，在定子繞組和轉子導條處，通過設定單元屬性實現場路耦合。在上文假設的條件下，設定電機各部件的材料屬性和模型的邊界條件，以異步電動機定轉子的整個圓面為求解區域，分別用兩種方法進行分析，即諧波分析和偽靜止瞬態分析。應用經典電機等效電路原理，在轉子回路用串聯的電阻代替負載的影響，即用s*σ子的電導率進行設置。通過改變轉差率，可得電機多種負載情況下的磁場分布和定轉子電流等。

4.1 諧波磁場分析

非線性時間—分析是基于能量等值方法用有效的B－H曲線代替實際的B－H曲線，將非線性的瞬態問題簡化成非線性時間－諧波問題［8］。在給定正弦電源時，磁通密度B被假定為隨時間成正弦變化的(在非線性瞬態分析中的磁通密度B是非正弦波形)，它只是真實磁通密度波形的時間基諧波近似值。圖6為異步電動機在空載情況下的實部和虛部磁力線分布圖;圖7為異步電動機在堵轉情況下的實部和虛部磁力線分布圖;從圖中可以看出，空載時，電動機的磁力線分布較好。在堵轉狀態下，轉子導條頂部的磁力線分布非常密集，即存在嚴重的集膚效應。

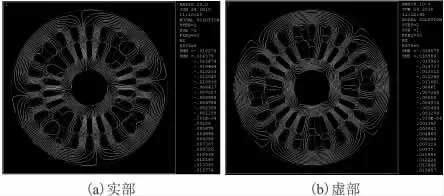
圖6 異步電動機在空載情況下的實、虛部磁力線分布

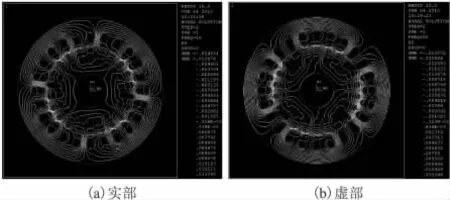
圖7 異步電動機在堵轉情況下的實、虛部磁力線分布

4.2 偽靜止瞬態分析

偽靜止瞬態分析與諧波相比，是使用了實際的BH磁化曲線［9］，并且在分析中考慮了場量的時間諧波的影響，能更精確的考慮磁飽和。其計算時間雖然比諧波分析更長，但與通用的時步有限元瞬態分析相比，已有較大的縮短。本文在進行偽靜止瞬態分析時，將時間步長設置為0.001s，仿真時間設為0～0.12s。

圖8是0.12s時電機在空載和堵轉狀態下的磁力線分布。圖9分別是仿真過程中，電機在空載和堵轉狀態下的定子電流分布情況。從圖中可以看出，定子三相電流經過一定的振蕩后基本穩定成正弦波，但三相電流的幅值并非完全相同(諧波分析時，定子三相電流的幅值也非完全相同)，這是由于在進行諧波分析和偽靜止瞬態分析中，都沒有考慮轉子旋轉時齒槽效應的影響。

圖8 0.12s時異步電動機空載和堵轉情況下的磁力線分布

圖9 異步電動機空載和堵轉時定子電流的分布情況

表2為電動機在空載和堵載下，定子A相電流有效值的諧波分析值、偽靜止瞬態分析值和實驗值對比表。從表中可以看出，偽靜止瞬態分析方法的分析誤差相對較小，但兩種分析方法都基本能滿足工程精度要求。

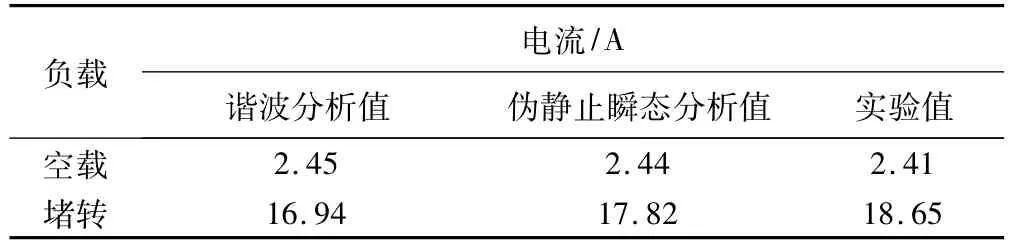
表2 定子電流對比表

在電動機的電磁場分析中，要采用哪種分析方法進行分析，需根據實際需要進行取舍。一般情況下，若只關心電機計算參數的平均值和有效值，如不涉及其變化過程，可以選擇諧波磁場分析。若更精確的考慮磁飽和，并且需要求出所需變量的變化過程，則可采用偽靜止瞬態分析法，該模型所耗機時雖比諧波磁場分析多，但與考慮電機旋轉時的時步有限元瞬態模型相比，所耗機時已少很多。

5 結論

本文建立了異步電動機的二維場路耦合有限元模型及其數學模型。分別利用諧波分析法和偽靜止瞬態分析法兩種方法對電動機進行電磁場分析，分別得到電動機在空載和堵轉兩種情況下的磁力線分布和定子電流。介紹兩種方法各自的特點，并將分析結果與實驗數據進行比較，精度滿足工程要求，從而驗證了所建電動機二維場路耦合有限元模型的正確性。通過此模型可以計算出與此電動機相關的很多特性參數，供電機的設計與分析使用，并為異步電動機的故障診斷和優化設計奠定基礎。

［1］ 胡石，武建文，李德成，等.小型電動機現代實用設計技術［M］.北京：機械工業出版社，2008.3.

［2］ H.De Gersem et al.Field-circuit coupled models in electromagnetic simulation.Journal of Computational and Applied Mathematics［J］ .2004：125－133.

［3］ 孫宇光，王祥珩，桂林，等.場路耦合法計算同步發電機定子繞組內部故障的暫態過程［J］.中國電機工程學報，2004，1(24)：136 －141.

［4］ 夏正澤，劉慧娟.基于場路耦合法的異步牽引電機電磁場分析［J］.微電機，2009，3(24).

［5］ 范鎮南，郭嘉.籠型異步電動機斷相運行的場路耦合時步有限元計算分析［J］.微電機，2009，(6).

［6］ 湯蘊璆.電機內的電磁場［M］.北京科學出版社，1998.

［7］ ANSYS Inc.Theory Reference.

［8］ 閻照文，等.ANSYS10.0工程電磁分析技術與實例詳解［M］.北京：中國水利水電出版社，2006.

［9］ 王愛龍，熊光煜.基于偽靜止瞬態二維有限元模型的異步電機穩態計算［J］.電氣應用，2006，3(25).