基于Bayesian非局部先驗的低劑量X-射線CT成像

高大志，陳陽，楊剛，盧光明

1.南京軍區南京總醫院 醫學影像科，江蘇 南京 210002；2.東南大學生物醫學工程學院醫學信息研究所，江蘇 南京 210000

基于Bayesian非局部先驗的低劑量X-射線CT成像

高大志1，陳陽2，楊剛1，盧光明1

1.南京軍區南京總醫院 醫學影像科，江蘇 南京 210002；2.東南大學生物醫學工程學院醫學信息研究所，江蘇 南京 210000

目的降低病人在CT掃描中所受的輻射劑量。方法在低劑量的掃描條件下，由于有效投影信息的缺少，CT圖像易受到量子噪聲的影響。本文提出了一種新的非局部先驗Bayesian重建算法來提高CT圖像重建質量。結果與傳統的圖像重建方法比較，本文提出的重建方法，能夠利用目標圖像中更多形態結構的全局信息來構建先驗項，從而克服了傳統圖像重建信息局限性的缺點。結論試驗證明本文所提出的CT圖像重建方法在低劑量掃描條件下具有很好的表現。

螺旋CT；CT成像；Bayesian；低劑量掃描

本文導讀 >>

課題背景：目前低劑量X-射線CT掃描由于能夠減少病人的掃描輻射傷害而日益受到人們的關注。課題受國家自然科學基金（No.81000636）資助，主要針對低劑量CT掃描中由于有效光子數降低而導致成像質量下降的問題所做的初步研究。

實驗設計/論文構思：基于Bayesian重建理論，通過引入圖像的全局信息來改善成像質量，并與當前國際上流行的其他圖像重建方法進行比較和分析。

1 研究背景

X-射線CT掃描在臨床上的廣泛應用，使得其中的輻射傷害日益受到人們的關注[1]。而目前螺旋CT掃描的普及也進一步增加了病人在掃描中所受的輻射劑量[2]。因此，低劑量掃描條件(降低參數mAs、電壓kV)下的CT成像越來越越多地得到醫生和病人的重視[3]。然而，采用傳統的FBP重建算法，在低劑量掃描條件下, 投影數據g容易受到量子噪聲的影響，重建出的圖像f質量會明顯下降，出現大量噪聲和星條狀偽影。基于統計學的迭代重建能夠針對系統模型的物理效應和探測數據、噪聲的統計泊松特性建立數學模型，同時可以通過Bayesian后驗定理引入圖像空間的先驗信息，解決圖像重建中由于噪聲而導致的病態問題，其重建的圖像質量要優于傳統的FBP方法[4-13]。Bayesian重建就是在迭代重建中引入圖像空間的先驗信息項來抑制噪聲，基于此，我們可以構建以下用于圖像重建的后驗概率：

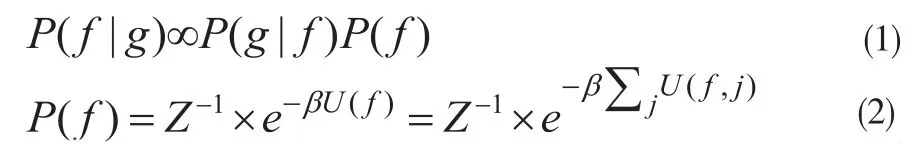
其中g和f分別為測量觀察數據和待重建的目標衰減圖像。P(f)代表馬爾可夫隨機場(Markov Random Fields，MRF)先驗分布。Z為正常數或者配分函數，為似然分布， 即為 MRF先驗能量或能量方程，為像素點處的先驗能量方程，全局參數β控制MRF先驗對重建圖像正則化作用的程度。可以根據(1)和(2)式建立相應的后驗能量方程：

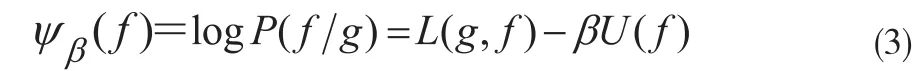
2005年，Buades等人設計了一種新的非局部去噪方法用于圖像的去噪處理[14]。在他們的非局部思想的啟發下，本文提出一個用于低劑量X-射線CT圖像Bayesian重建的非局部二次先驗模型，該模型不僅能使用目標圖像中單個像素之間的灰度差信息，而且能夠有效的利用圖像中連接和連續的全局信息。相關的模擬試驗表明：對于低劑量投影數據的X-射線CT圖像重建，本文所提出的非局部先驗Bayesian重建法在降低噪聲效果和保持邊緣方面均具有非常好的表現。

1.1 傳統局部先驗模型

基于MRF理論，當目標圖像f滿足先驗假設時，公式(2)中的能量方程U(f)具有最小值且相應的先驗分布(2)式達到最大值。而像素j點處的先驗能量方程U(f,j)通常等于以像素j與其鄰域Nj內個點的差為自變量的勢能函數v( )的加權和：

可以通過選擇不同的勢能函數v(t)來設計用于Bayesian重建的不同先驗模型。如果勢能函數v(t)為二次的V(t)=t2形式，先驗P（f）即為簡單的二次QM平滑先驗。我們也可通過使用選擇一些非二次勢能函數v(t)來使用非二次先驗[3-10]，如Huber先驗的勢能方程：

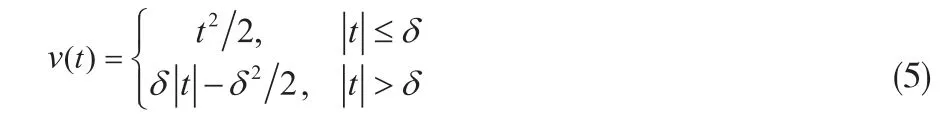
其中，δ為控制勢能函數的閾值參數。

公式(4)中的權值量wbj為表示圖像中像素b和j的相互關系的正常數。通常設定wbj的值同像素b和j之間距離成反比。下面即為廣泛應用于圖像重建和恢復中的傳統局部先驗的八鄰域歸一化權值圖和四鄰域歸一化權值圖:

以上的先驗模型只能為圖像重建提供固定的局部的先驗信息。二次局部QM先驗通過重建過程中的一個平均化的作用提供平滑的先驗信息，從而易于導致圖像邊緣細節和噪聲同時平滑掉的過平滑效應。具有邊緣保持作用的局部非二次先驗則會因為無法有效的區分噪聲和一些較細微的細節而為圖像重建帶來負面的偽影效果。

1.2 非局部二次先驗模型

在建立非局部先驗的過程中，一方面需要選擇一個較大的鄰域來包含圖像中的更多幾何形態信息，另一方面通過計算像素b的鄰域和j的鄰域的一個相似性測度，而不是用以上1.1節所述的像素間二維空間距離的簡單反比例量來計算權值wbj。根據以上的非局部先驗設計思路，我們可以根據(6)～(11)式為Bayesian重建設計新的非局部先驗。

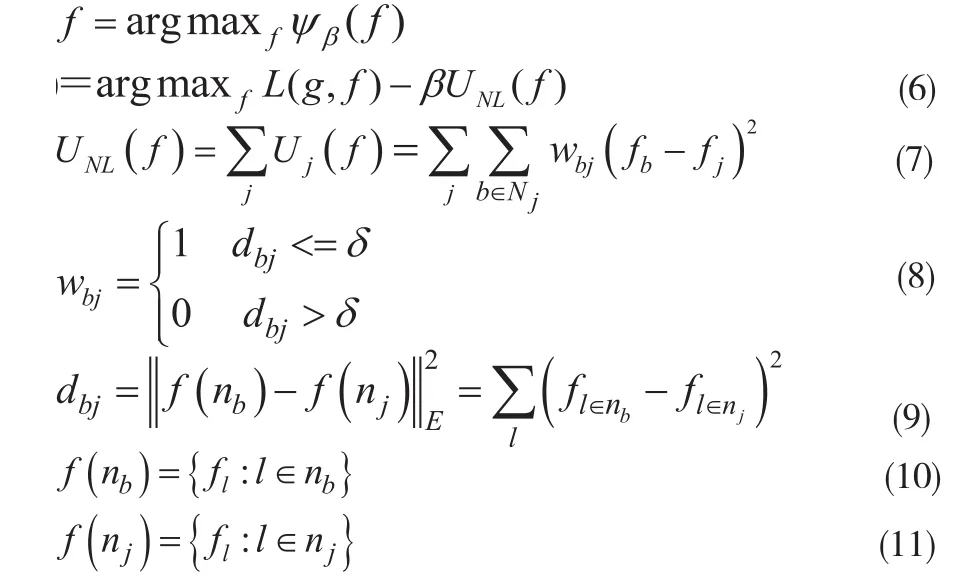
式中UNL(f)為非局部先驗的能量函數， 這里Nj通常選擇一個較大尺寸的鄰域以引進更多的結構信息，wbj設為（1-0）二值函數，代表先驗中像素b和j之間的權值，nb和nj為設定的以像素b和j為中心的方形鄰域， f(nb)和f(nj)為此兩個鄰域中所有像素灰度值數組，‖f（nb）-f（nj）‖代表此兩個像素灰度值數組的加權歐幾里得距離。

在選擇一個較大鄰域的基礎上，此非局部先驗不僅比較圖像中兩個像素的灰度值，而且通過比較此兩個像素鄰域的相似性來計算勢能函數中的權值量。如圖1所示，在每組圖中，左邊的圖為原圖，右邊的圖描繪了左圖中心點鄰域中各點在非局部先驗模型中權值的取值情況。可以看出，權值一般分布于比較相似的結構處，對于兩個具有相似周圍結構的像素點，此兩個像素點在先驗中的權重較大，該非局部先驗模型能夠考慮到圖像中的一些較大的幾何結構形態的全局信息，能夠對圖像重建中的病態問題提供更為有效的正則化。

圖1 權值分布圖

在使用文中所述的非局部先驗模型的情況下，目標圖(每組圖中左圖)中的中心點的鄰域權值分布如每組圖中的右圖所示，設定nb和nj的大小分別為31×31和7×7時，(a) 當中心點位于一條豎直的邊緣上時，權值分布在此豎直邊緣線上；(b) 當中心點位于傾斜的邊緣時，權值分布在傾斜的邊緣線上；(c) 當中心點位于特定紋理結構時，權值分布在特定的紋理結構上。

2 實驗與分析

2.1 CT迭代重建

在X-射線CT重建中，我們可以把測量投影數據理解為服從獨立泊松分布的隨機變量。第i對投影數值gi可以認為是一個期望的泊松隨機數，這個是一個自變量為衰減圖像的方程[7-8]。似然方程PL(g/f)定義為在已知f的情況下，得到測量數據g的概率。基于此，可以得到以下各式：

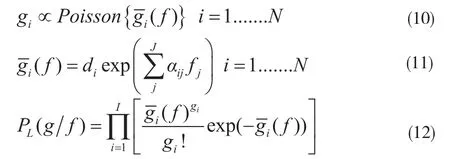
其中N是探測器對的數目，j是目標圖像像素的數目，αi,j是在理想條件下圖像像素點j被探測器對i探測到的幾何概率。f2(g/f)對應于(1)中P(g/f)，其對數似然能量方程為：

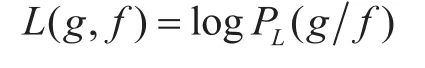
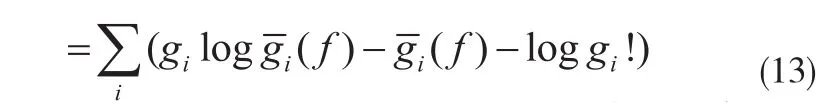
可以通過對后驗能量ψ的最大化迭代運算來重建出目標圖像f：

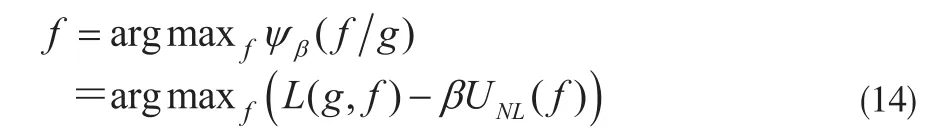
然而，由(7)～(11)式可知，此非局部先驗能量中的權值項wbj的取值由目標圖像f所決定，增加了直接求導計算的難度，實際試驗我們采用如下步驟的重建算法：

（1）設定迭代初始項f°。

（2）權值項w的更新：在構建此非局部先驗能量時，對于目標圖像f中的每一個像素對(fb，fj)，用迭代過程中的當前值的和公式(7)～(11)來計算wbj。

（3）目標圖像f項的更新：

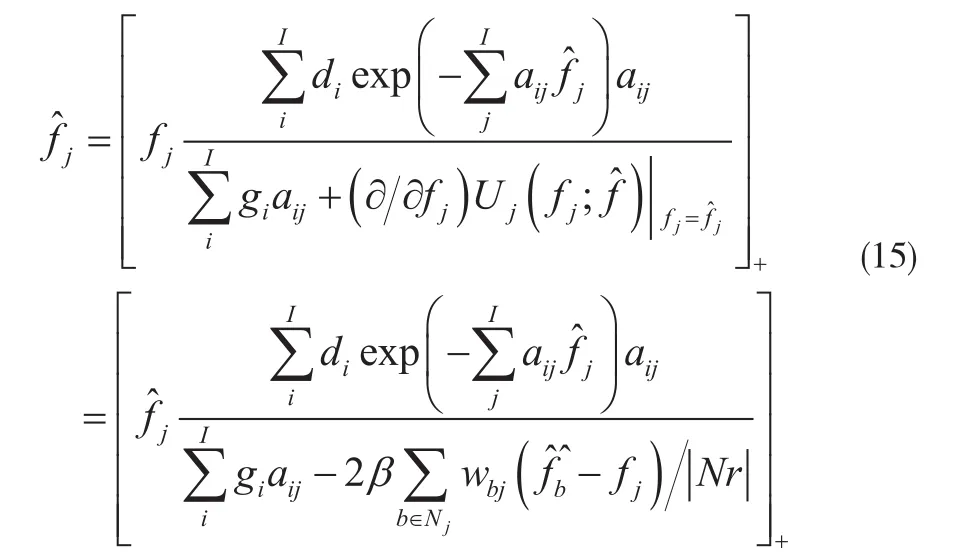
2.2 模擬試驗

在實驗中,我們使用單排探測器CT，X-射線源和探測器距離設為100cm，旋轉中心到探測器距離設為40cm，相鄰探測器距離為1mm，掃描系統為具有367個徑向取樣和360個角采樣的系統。圖2 (a)為試驗中使用的256×256體模數據圖像，表示一個Shepp-Logan體模截面圖，圖像素點取值范圍為0～240；圖2(b)為對應的正弦圖（sinogram）投影數據。基于此模擬的兩個不同劑量(投影數據數值總和分別為1.2×108和1.5×108)的投影數據，投影數據中均加入了10%服從泊松分布的隨機噪聲。轉換概率矩陣A為一個平行帶狀積分幾何模型，通過(12)式中的模型進行計算。

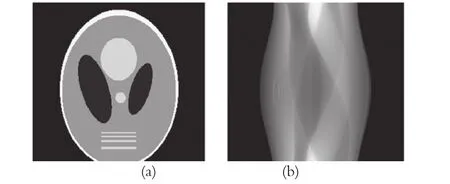
圖 2 體模圖像(a)與對應的平行束投影正弦圖(b)

圖3和圖4分別顯示了使用以上的兩個不同劑量投影數據下的重建結果，使用Ramp濾波器的FBP重建(FBP1重建)，使用Hann濾波器的FBP重建(FBP2重建)和使用二次局部QM平滑先驗，非二次局部Huber先驗，MRP以及非局部先驗的Bayesian重建圖像。對于后面4種Bayesian重建，選取第250次迭代的重建圖 (在實驗中，當迭代到第250次時，重建圖像已趨于穩定)。從圖3和圖4可以看到 探測數據在FBP重建圖像中易出現大量噪聲和星條偽影，相對于使用Ramp濾波器的FBP1重建(圖3 (a)和圖4 (a))；使用Hann濾波器的FBP2重建(圖3 (b) 和圖4(b))能夠更好的抑制噪聲；采用QM先驗重建的圖像(圖3 (c) 和圖4(c))中出現了導致結構信息模糊的過平滑效應；對于使用非二次Huber先驗的重建(圖3 (d) 、圖4 (d))和MRP(圖3 (e) 、圖4 (e))的重建來說，可以從結果圖像中觀察到塊狀的不規則偽影區域和階梯狀的偽影。另一方面，可以清楚的觀察到，使用本文提出的非局部先驗重建的圖像(圖3 (f)和圖4 (f))具有更加均勻的背景區域和更加清晰的邊緣。采用該非局部先驗的重建不僅能夠克服QM平滑先驗的過平滑效應，而且能夠在很大程度上解決非二次Huber先驗和MRP所導致的階梯狀偽影的問題。

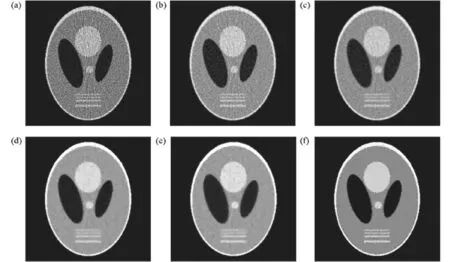
圖 3 使用總和為1.2×108探測數據sinogram的重建結果

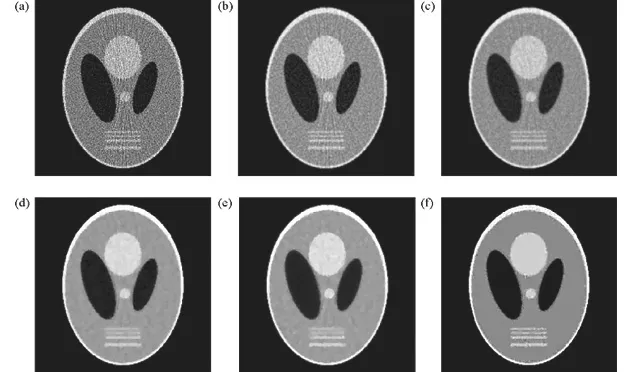
圖 4 使用總和為1.5×108探測數據sinogram的重建結果

在重建試驗中，使用不同的體模數據需要選擇不同的參數，試驗中依據產生最高信噪比SNR（計算公式見(16)）的原則手工設定參數，試驗中，信噪比SNR的計算公式為：

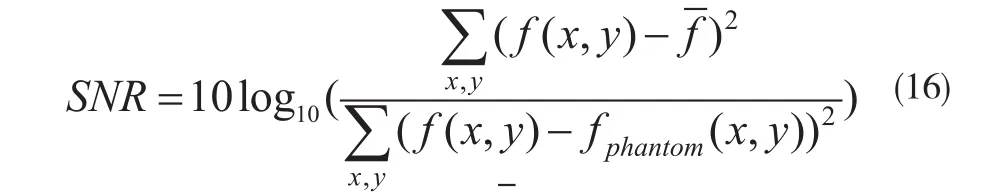
對于此兩種不同計數量的sinogram數據，在二次QM先驗重建中，設定全局參數β的值分別為2×10-2和1.8×10-2；在采用非二次Huber先驗的重建中，全局參數的值同QM一樣，設定全局參數δ的值分別為1.6和1.3；在采用MRP的重建中，設定全局參數β的值分別為40和20；在采用非局部先驗的重建中，設定全局參數β的值分別為0.5和0.6，式(6)～(8)中參數n的取值分別為0.6和1.1，設定式(6)中nj的大小為11×11，設定(9)～(10)中的兩個比較鄰域nb和nj的大小為7×7。

表1給出了對于此兩種不同計數量的sinogram數據。由以上所有重建圖像對于真實體模圖像的信噪比SNR，可以看出使用本文提出的方法的重建圖像具有更高的信噪比。表2給出了不同重建方法在P4 1.6 GHz、512Mb RAM 的硬件環境下，matlab7.0的軟件環境下運行得到重建結果所需的CPU時間。可以看出本文所提出的非局部先驗Bayesian重建需要更多的計算時間。

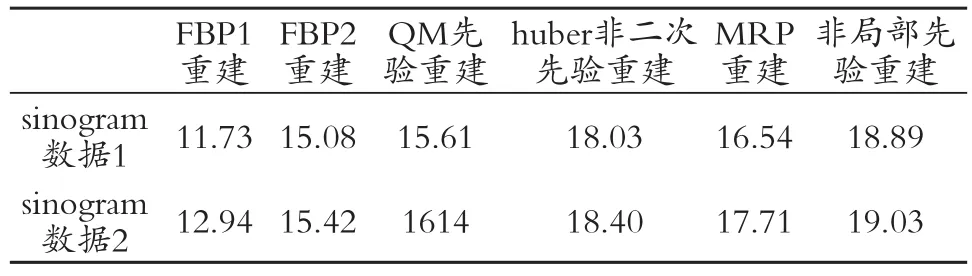
表1 兩種不同總探測量的sinogram數據，重建圖像相對于圖2中真實體模圖像數據的信噪比

表2 重建中使用不同方法所需CPU時間(s)

3 結論

相對于通常意義上的二次或者非二次的局部先驗，本文提出的新的非局部先驗能夠利用目標圖像中更多形態結構的全局信息來構建先驗項，能夠引入更多更全面的先驗信息，從而克服了局部先驗信息局限性的缺點。基于模擬數據和真實數據的試驗表明：相對于使用普通的二次平滑先驗及非二次邊緣保持先驗的重建，使用該混合先驗重建的CT圖像能夠更好保持邊緣信息，消除背景噪聲，且具有更高的信噪比。

進一步的工作包括，對圖像重建中由非局部先驗引進的參數進行有效的估計，減少使用非局部先驗重建的計算量；應使用更多的真實CT圖像掃描數據來測試該非局部先驗重建方法在臨床試驗中的效果。

[1]Linton OW, Mettler Jr FA. National conference on dose reduction in CT, with an emphasis on pediatric patients[J]. Am JRoentgenol,2003,181:321-329.

[2]Jung K, Lee K, Kim S, et al. Low-dose, volumetric helical CT:image quality, radiation dose, and usefulness for evaluation of bronchiectasis[J]. Invest Radiol,2000,35:557-563.

[3]Lu H, Hsiao I, Li X, et al. Noise properties of low-dose CT projections and noise treatment by scale transformations[C].2001 IEEE Nuclear Science Symp.Conf.,2001.p.1662-1666.

[4]Beekman FJ,Kamphuis C.Ordered subset reconstruction for X-ray CT[J]. PhysMed Biol,2001,46:1835-1855.

[5]Stan Z. Li. Markov Random Field Modeling in image Analysis[M]. Tokyo: Springer-Verlag, 2001:1-40.

[6]Black. M. J and Rangarajan A. Unification of line process,outlier rejection, and robust statistics with application in early vision [J]. Int. Journal of Computer Vision, 1996, 9:57-91.

[7]Nuyts J, De Man B, Dupont P, et al. Iterative reconstruction for helical CT:a simulation study[J].Phys Med Biol,1998,43:729-737.

[8]Sukovic P, Clinthorne NH. Penalized weighted leastsquares image reconstruction in single and dual energy X-ray computed tomography[J].IEEE Trans Med Imaging,2000,19(11):1075-1081.

[9]Lange K.Convergence of EM image reconstruction algorithms with Gibbs smoothness[J]. IEEE Trans Med Imaging,1990,9:439-446.

[10]Erdo-gan H, Fessler JA.Monotonic algorithms for transmission tomography[J]. IEEE Trans Med Imaging,1999,18(9):801-814.

[11]Alenius S, Ruotsalainen U, Astola J. Attenuation correction for PET using countlimited transmission images reconstructed with median root prior[J]. IEEE Trans Nucl Sci,1999,46:646-651.

[12]Yu DF, Fessler JA.Edge-preserving tomographic reconstruction with nonlocal regularization[J].IEEE Trans Med Imaging,2002,21(2):159-173.

[13]Li SZ. Markov random field modeling in image analysis[M].Tokyo: Springer-Verlag,2001:1-30.

[14]Buades A, Coll B, Morel JM. A nonlocal algorithm for image denoising[J]. Proc IEEE Int Conf Comput Vision Pattern Recognit,2005,2:60-65.

[15]Chen Y,Ma J,Feng Q,et al.Nonlocal prior Bayesian tomographic reconstruction[J]. J Math Imaging Vision,2008,30:133-146.

[16]周顯國,等.貝葉斯決策分析在醫學步態分析中運動目標檢測的應用研究[J].中國醫療設備,2010,25(9):16-19.

Low-dose X-ray Computed Tomography Based on Bayesian Nonlocal Prior

GAO Da-zhi1, CHEN Yang2,YANG Gang1, LU Guang-ming1
1.Medical Imaging Department, Nanjing General Hospital of Nanjing Military Area Command, Nanjing Jiangsu 210002,China;2.Institute of Medical Information&Technology, School of Biomedical Engineering, Southeast University, Nanjing Jiangsu 210000,China

R319；TN919.81

A

10.3969/j.issn.1674-1633.2011.02.006

1674-1633(2011)02-0021-04

2010-10-20

2010-11-23

國家自然科學基金（81000636）資助。

本文作者：高大志，碩士研究生。

作者郵箱：njdazhi@hotmail.com

Abstract:ObjectiveTo reduce the radiation dose delivered to the patients during the application of computed tomography (CT).MethodsCT images can be easily degraded by the quantum noise under low X-ray dose scan protocols. Statistical reconstructions outperform the traditional filtered back-projection(FBP) reconstructions by accurately modeling the scan system and the measurement statistics. This paper aims to improve the CT reconstruction using a new nonlocal prior statistical reconstruction approach.ResultsCompared to traditional reconstruction approaches, the proposed nonlocal prior can impose an effective regularization for reconstructions by exploiting the image global information adaptively.ConclusionExperimentation validates that the proposed CT reconstructions have excellent performance with low-dose scan protocols.

Key words:spiral CT; CT imaging; Bayesian arithmetic; low-dose scanning