基于DSA和FEM的電器絕緣結(jié)構(gòu)自動優(yōu)化設(shè)計

馬愛清，張周勝

(上海電力學(xué)院電力與自動化工程學(xué)院，上海 200090)

電器裝置自動設(shè)計中，形狀優(yōu)化設(shè)計在改進電磁設(shè)備性能方面非常重要.根據(jù)尋優(yōu)過程的不同，優(yōu)化方法可以分為隨機性優(yōu)化和確定性優(yōu)化兩種.隨機性優(yōu)化方法包括基因算法、TABU算法和模擬退火法等，由于能給出全局優(yōu)化解，在過去的十幾年內(nèi)，已被廣泛應(yīng)用于各種電磁工程設(shè)計［1-3］.確定性優(yōu)化方法，比如結(jié)合設(shè)計靈敏度分析的梯度法，盡管有時會陷入局部極小，但由于可以大幅度地降低尋優(yōu)過程中目標(biāo)函數(shù)的計算次數(shù)，最大限度地降低尋優(yōu)過程中的計算代價，從提高計算量的角度，結(jié)合設(shè)計靈敏度分析的確定性方法更優(yōu)于非確定性方法［4-6］.本文將靈敏度分析(Design Sensitivity Analysis，DSA)、有 限 元 法(Finite Element Method，F(xiàn)EM)以及優(yōu)化算法相結(jié)合，對2D電器裝置的形狀進行優(yōu)化，給出了設(shè)計靈敏度分析公式及伴隨變量方程的推導(dǎo)，并將該方法成功用于110 kV GIS光纖電流互感器的絕緣結(jié)構(gòu)優(yōu)化設(shè)計中.

1 結(jié)構(gòu)優(yōu)化模型

將結(jié)構(gòu)模型、設(shè)計靈敏度分析和優(yōu)化算法結(jié)合成為一個通用的系統(tǒng)，實現(xiàn)各種優(yōu)化自動設(shè)計是非常必要的.圖1所示的結(jié)構(gòu)優(yōu)化模型表示了形狀優(yōu)化設(shè)計問題的3個組成部分.

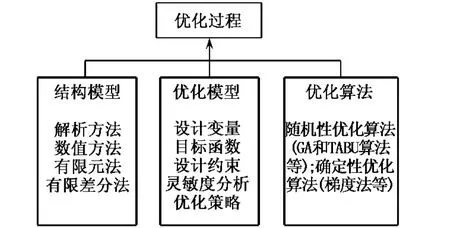
圖1 結(jié)構(gòu)優(yōu)化模型示意

結(jié)構(gòu)模型提供在靜態(tài)或動態(tài)邊界條件下結(jié)構(gòu)的性能特性.結(jié)構(gòu)參數(shù)是在構(gòu)造目標(biāo)函數(shù)及設(shè)計約束時用到的設(shè)計變量.在實際工程應(yīng)用中，需要建立詳細(xì)的有限元模型.優(yōu)化模型將結(jié)構(gòu)分析與優(yōu)化算法相聯(lián)系，目標(biāo)函數(shù)值與性能約束值通過結(jié)構(gòu)模型的有限元分析得到.而優(yōu)化模型中所定義的目標(biāo)函數(shù)最優(yōu)解可通過優(yōu)化算法求得.

2 2D靜電場問題設(shè)計靈敏度分析

2D靜電場的系統(tǒng)控制方程為:

式中:ε——介電常數(shù);

φ——電勢.

靜電場的有限元分析可以最終歸結(jié)為求解如下有限元方程:

式中:A——系統(tǒng)矩陣;

X——電位矩陣;

b——載荷向量矩陣.

靜電場的形狀優(yōu)化設(shè)計都可以表示為:

式中:F——目標(biāo)函數(shù);

p——由表面節(jié)點組成的設(shè)計參數(shù)向量;

X——狀態(tài)變量;

pmax，pmin——設(shè)計參數(shù)的上下限值.

關(guān)于設(shè)計變量的靈敏度可以推導(dǎo)如下:

對式(2)兩邊的設(shè)計變量p求導(dǎo)，并乘以伴隨變量 λT［7，8］，可以得到:

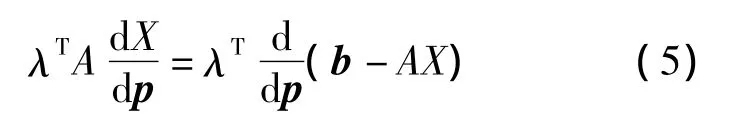
通過選擇伴隨變量，使得式(4)和式(5)中的dX/dp系數(shù)相等，因此可以得出伴隨方程和靈敏度公式為:

式中的X就是式(2)的解.

根據(jù)最速下降法，利用已計算得到的靈敏度來更新設(shè)計變量:

式中:α——松弛因子.

3 有限元網(wǎng)格更新方法

形狀優(yōu)化設(shè)計的一個重要部分是隨著設(shè)計變量的改變來更新有限元網(wǎng)格，并且應(yīng)盡量使有限元網(wǎng)格均勻分布，它是保證計算結(jié)果精度的重要因素［9］.

采用Delaunay三角剖分技術(shù)所形成的三角形網(wǎng)格，最小的內(nèi)角是所有三角剖分中最大的，而且Delaunay三角剖分所形成的三角形最接近于等邊三角形，因此該技術(shù)在實際應(yīng)用中具有很大優(yōu)勢.其基本思想是:首先形成只有邊界節(jié)點構(gòu)成的開端網(wǎng)格，在此基礎(chǔ)上，引進一個新節(jié)點，根據(jù)原判據(jù)修改原來的網(wǎng)格，以形成新網(wǎng)格;在新網(wǎng)格的基礎(chǔ)上，再引進一個新節(jié)點形成新網(wǎng)格，依此循環(huán)直至引進全部節(jié)點.但節(jié)點的分布直接影響網(wǎng)格的優(yōu)劣，在網(wǎng)格更新過程中，需要利用邊界節(jié)點分布來有效控制內(nèi)部節(jié)點的分布，以實現(xiàn)網(wǎng)格疏密連續(xù)過渡，避免出現(xiàn)太尖或太鈍的三角形單元.

因此，可以采用基于Delaunay三角剖分的置換算法(Swapping Algorithm)［10］.由于設(shè)計變量的改變，網(wǎng)格需要更新，如圖2所示，邊界單元較長的邊上有可能產(chǎn)生新點P，而置換算法根據(jù)對角線的長度來修正P點的位置，盡可能地減少三角形網(wǎng)格的變形.

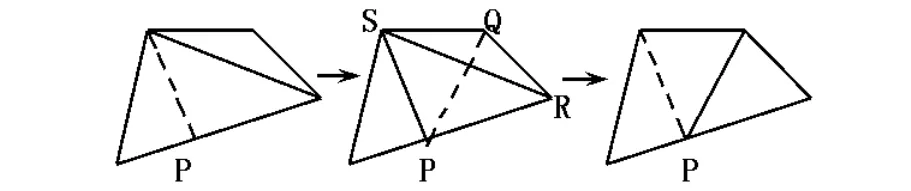
圖2 網(wǎng)格更新中節(jié)點位置的修正

在設(shè)計變量改變后，需要對網(wǎng)格進行更新，在網(wǎng)格生成程序中采用Delaunay三角剖分算法和置換算法，所有的設(shè)計參數(shù)點可以被指定為單元邊界的初始點，在每次優(yōu)化迭代后，被改變的設(shè)計參數(shù)自動輸入，作為邊界的初始點，以產(chǎn)生新的網(wǎng)格.

4 優(yōu)化算法流程

將有限元分析、最速下降法和網(wǎng)格更新方法相結(jié)合，形成新的2D形狀優(yōu)化設(shè)計算法，見圖3.

圖3 優(yōu)化算法流程

顯然，該優(yōu)化設(shè)計算法僅需要進行有限元網(wǎng)格一次剖分，就可以大大縮短計算周期，節(jié)約優(yōu)化設(shè)計的計算量.

5 GIS光纖CT絕緣結(jié)構(gòu)自動設(shè)計

在電磁裝置的自動設(shè)計中，靈敏度分析及有限元技術(shù)已得到廣泛的應(yīng)用［11，12］.圖4為110 kV GIS光纖CT絕緣結(jié)構(gòu)中的一相高壓電極簡化模型.設(shè)計中，B可以在30～60 mm之間調(diào)整，R可以在10～25 mm之間調(diào)整.

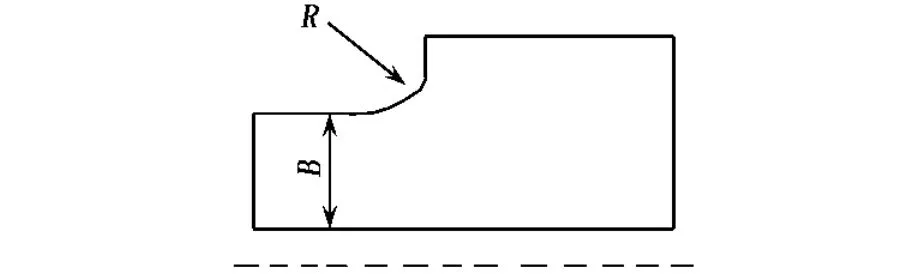
圖4 110 kV光纖CT絕緣結(jié)構(gòu)示意

在絕緣結(jié)構(gòu)設(shè)計中，靜電場絕緣外表面期望的最大電場強度值可以由設(shè)計人員提出.

該設(shè)計中，目標(biāo)函數(shù)定義為:

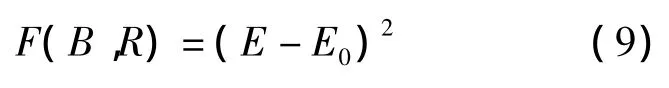
式中:E——絕緣外表面電場強度的最大值;

E0——所期望的電場強度設(shè)定值，當(dāng)在高壓電極和低壓電極施加275 kV的電壓時，希望得到 E0=9.0 kV/mm的設(shè)計值.

利用本文提到的靈敏度設(shè)計方法自動設(shè)計，通過5次迭代，當(dāng)B=45 mm，R=20 mm時，得到了所期望的電場強度設(shè)計值E0=9.0 kV/mm.

為了檢驗設(shè)計的正確性，又通過有限元法求解該靜電場，解得的結(jié)果為9.07 kV/mm.該結(jié)果與本文利用優(yōu)化設(shè)計方法所得結(jié)果相比，二者的相對誤差為0.7%，表明上述自動設(shè)計程序是有效的.

6 結(jié)語

在有限元方法的基礎(chǔ)上，本文給出了2D靜電場靈敏度分析設(shè)計的公式推導(dǎo)，以及整個優(yōu)化算法的流程框圖，通過計算目標(biāo)函數(shù)對幾何變量的靈敏度，來優(yōu)化設(shè)計電器裝置的絕緣結(jié)構(gòu).通過實例表明，本文所用方法在快速優(yōu)化計算的同時，還可以保證計算結(jié)果的精度.

［1］汪友華，陳敏，劉福貴，等.改進的遺傳算法及其在SF6滅弧室永磁場優(yōu)化中的應(yīng)用［J］.中國電機工程學(xué)報，2001，21(10):43-46.

［2］楊仕友，倪光正，錢金根.電機電磁場的逆問題數(shù)值計算的改進TABU算法［J］.中國電機工程學(xué)報，1998，18(2):83-86.

［3］楊仕友，倪光正.模擬退火算法的改進及其在電機電磁場逆問題數(shù)值計算中的應(yīng)用［J］.電工技術(shù)學(xué)報，1998，13(2):21-23.

［4］WANG S，KANG J.Shape optimization of BLDC motor using 3D finite element method［J］.IEEE Trans.on Magnetics，2000，36(4):1 119-1 123.

［5］BYUN Jin-kyu，LEE Ju-hyun，PARK Il-han，et al.Inverse problem application of topology optimization method with mutual energy concept and design sensitivity［J］.IEEE Trans.on Magnetics，2000，36(4):1 144-1 147.

［6］OKAMOTO Y，AKIYAMA K，TAKAHASHI.3D topology optimization ofsingle-pole-type head by using design sensitivity analysis［J］.IEEE Trans.on Magnetics，2006，42(4):1 087-1 090.

［7］IOAN D，MUNTEANU I，CIUPRINA G.Adjoint field technique applied in optimal design of a nonlinear inductor［J］.IEEE Trans.on Magnetics，1998，34(5):2 849-2 852.

［8］GITOSUSASTRO S，COULOMB J C，SABONNADIERE J C.Performance derivative calculations and optimization process［J］.IEEE Trans.on Magnetics，1989，25(4):2 834-2 839.

［9］盛劍霓.工程電磁場數(shù)值分析［M］.西安:西安交通大學(xué)出版社，1991:65-95.

［10］LAWSON C L.Software for C1interpolation in mathematical software III［M］.New York:Academic press，1977:35-42.

［11］RAMIREZ J A，F(xiàn)REEMAN E M.Sensitivity analysis for the automatic shape design of electromagnetic devices in 3D using FEM ［J］.IEEE Trans.on Magnetics，1997，33(2):1 856-1 859.

［12］CUI Xiang，ZHANG Guo-qiang.Sensitivity analysis and automatic design of voltage ratio in an optical instrument voltage transformer［J］.IEEE Trans.on Magnetics，1999，35(3):1 769-1 772.