單相逆變器迭代學習控制應用研究

葉建華，曹 旭

(上海電力學院電力與自動化工程學院，上海200090)

在日益興起的分布式發電系統研究中，逆變器作為廣泛采用的能量轉換及接口器件，其性能對于分布式發電系統的穩定、高效運行起著十分重要的作用.逆變器輸出波形的質量是衡量逆變器性能的重要指標［1］.單純采用 PID控制的PWM逆變器存在跟蹤正弦波形不精確，易受非線性負載影響造成電壓、電流畸變等不利因素.

迭代學習控制(Iterative Learning Control，ILC)著眼于利用受控對象和目標軌道的周期性或重復性，起初應用在重復性機械運動結構的控制中，由于其不需要依賴控制對象的精確數學模型、結構簡單，以及具有良好的跟蹤精度等特點獲得了廣泛的關注.本文將迭代學習控制應用于逆變器輸出波形的控制，以期解決逆變器跟蹤正弦波形不精確等問題.

1 迭代學習控制

迭代學習控制的基本思想是:在被控系統作重復運動且結構特性不變的前提下，利用控制器先前的控制經驗逐漸尋找理想的輸入特性曲線，使被控對象精確地按期望軌跡運動［2，3］.于是可將一重復運動軌跡(如正弦波)按周期分為若干次控制過程，如圖1所示.

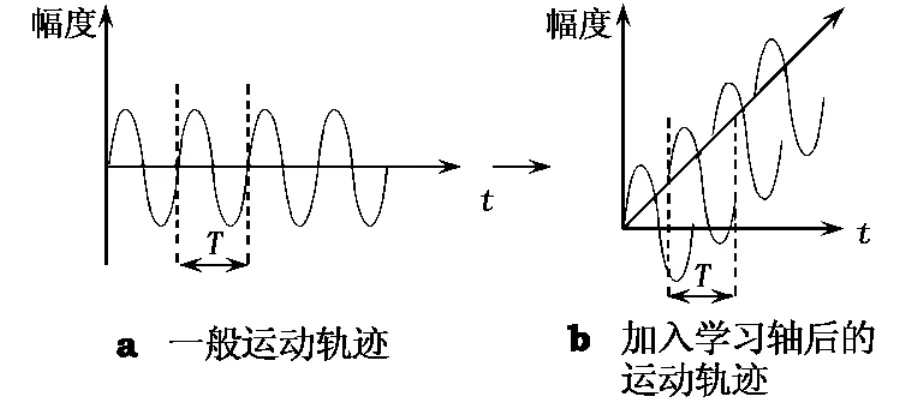
圖1 學習控制基本思想

迭代學習跟蹤控制的目標是要獲得一個控制序列ud(n)，使得系統輸出y(n)精確跟蹤理想輸出yd(n).迭代學習的基本原理是利用上一次工作周期內的誤差ek(n)，對下一次工作周期的控制輸入uk+1(n)進行修正，經過多個工作周期的學習，逐漸使實際輸出y(n)收斂于理想輸出yd(n).

迭代學習的控制算法有:PID型學習算法，高階迭代學習算法，具有遺忘因子的學習算法，基于2-D系統理論的學習算法等［3］.PID型學習算法分為開環學習和閉環學習.開環PID學習算法是第k+1次的控制等于第k次的控制加上第k次輸出誤差的PID校正項，即:

式中:kp——比例;

kd——微分;

ki——積分學習增益.

閉環PID學習算法是取第k+1次運行的誤差作為學習的修正項，即:

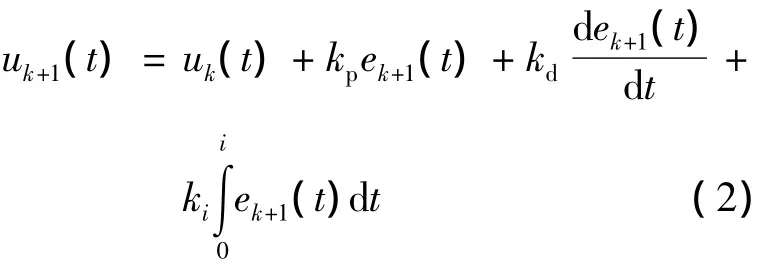
按照學習方式的不同，PID型學習算法可分為開環學習和閉環學習［2，4］:前者是指每次控制指令的大小只和前一次控制指令及前一次軌跡誤差相關，與當前的軌跡誤差無關;后者是指每次控制指令的大小只與前一次控制指令及當前的誤差軌跡相關.這兩種學習方式的控制框圖見圖2和圖3.在傳統學習控制中學習方式可選擇P型、PI型和 PID 型等［2，3］.

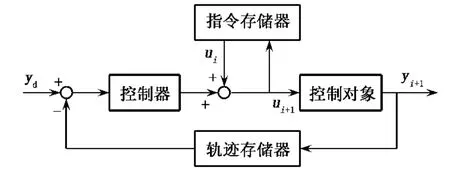
圖2 開環學習控制

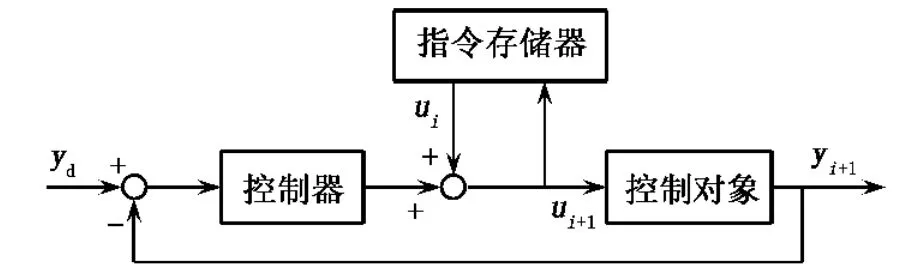
圖3 閉環學習控制

2 P型學習率的收斂性判定

收斂性是迭代學習控制理論的中心問題.學習算法的穩定性是保證學習控制能夠運行的基本前提，其作用是隨著學習次數的增加，保證控制系統不發散.但對于學習控制系統而言，僅僅穩定是不夠的，只有使學習過程收斂到真值，才能保證得到的控制為某種意義下的最優控制.目前，從最初的時不變系統到線性時變系統再到非線性系統，從連續系統到離散系統都有大量的具有穩定性和收斂性的學習律［3］.

對于P型學習控制的開環學習收斂定理，考慮如下的連續系統:

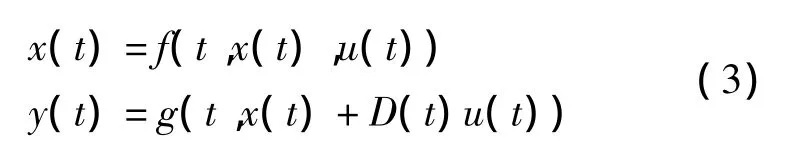
若采用如下開環P型學習律

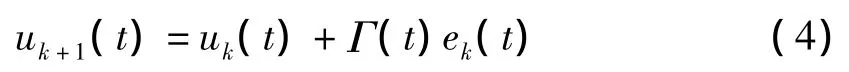
系統式(3)在t∈［0，T］中需滿足下列條件:

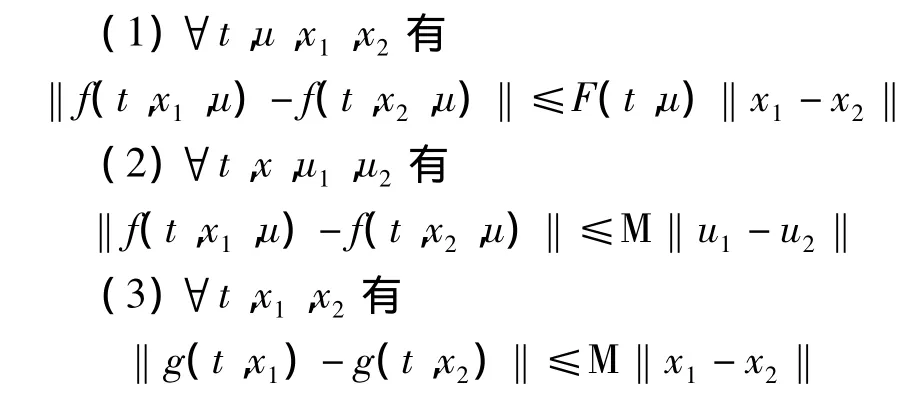
(4)每次運行時的初始誤差{δxk(0)}k≥0為一收斂到零的序列;

(5)存在唯一的理想控制ud(t)使得系統的狀態和輸出為期望值xd(t)，yd(t)，其中 F(t，u)為t，u的連續函數，M為一正的常數.

此時，對于任意給定的初始控制u0(t)及每次運行的初始狀態xk(0)所得序列皆對t一致地收斂到xd(t)，yd(t)，ud(t)的充分條件為譜半徑:

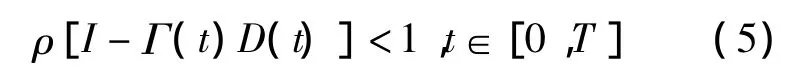
其必要條件為:

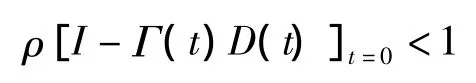
若Γ(t)，D(t)為常數矩陣，則式(5)成為充分必要條件.

若采用閉環學習收斂定理，考慮系統為式(3)，則有:

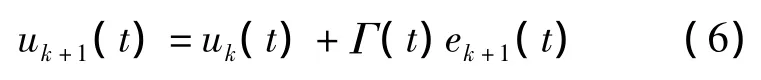
系統式(3)在t∈［0，T］中滿足下列條件:

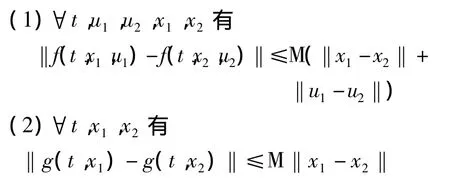
(3)每次運行時的初始誤差{δxk(0)}k≥0為一收斂到零的序列.

(4)存在唯一的理想控制ud(t)使得系統的狀態和輸出為期望值xd(t)，yd(t).

(5)(I+Γ(t)D(t)－1)存在，(1)至(2)中的M為一正的常數，則對于任意給定的初始控制u0(t)及每次運行的初始狀態xk(0)，所得的序列皆對t一致地收斂到xd(t)，yd(t)，ud(t)的充分條件為譜半徑

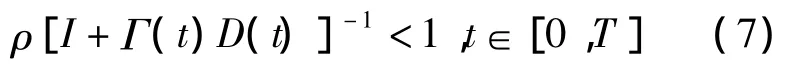
其必要條件為

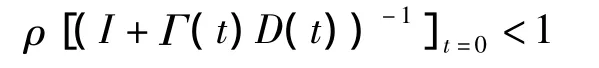
若Γ(t)，D(t)為常數矩陣，則式(5)成為充分必要條件.

3 仿真比較

3.1 系統結構

逆變器的控制結構為傳統的雙環PWM控制，由于非線性負載的存在，會使得逆變器的輸出電壓波形產生畸變.本文在電壓外環上采用ILC控制器取代傳統的PID控制器.ILC控制器又分別采用比例型開環學習和比例型閉環學習兩種形式，并將其效果與PID控制器效果進行比較.所采用的主系統參數為:直流母線電壓400 V，輸出交流電壓的有效值為220 V，頻率為50 Hz，負載為二極管整流型負載，其系統結構見圖4.

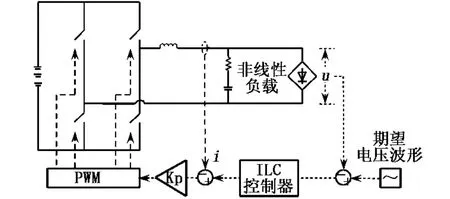
圖4 系統結構示意

3.2 仿真波形

當電壓外環采用PID控制器時，逆變器輸出波形U出現了明顯的畸變，電壓有效值跌落至199 V，總諧波含量THD達到了7.6%.

當采用開環學習型ILC控制器后，逆變器的輸出波形有了一定的改善，電壓有效值恢復至218 V，總諧波含量THD降至4.8%.但是開環學習型ILC的輸出只與上一周期的輸出及誤差有關，因此控制器作用會有一個周波的延遲，如圖5所示.

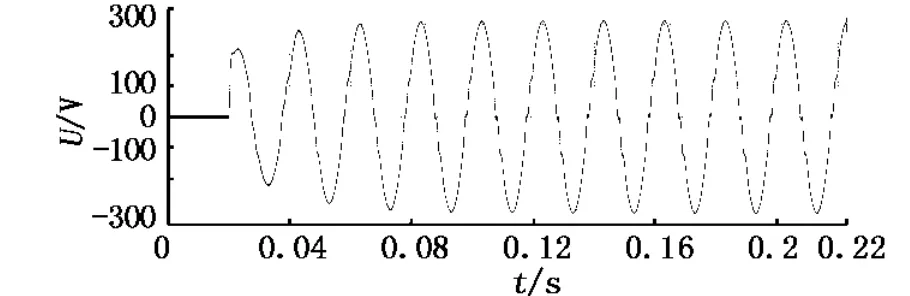
圖5 采用開環學習ILC控制器時輸出電壓U波形

當采用閉環學習型ILC控制器后，逆變器的輸出波形獲得了較大的改善，電壓有效值恢復至220 V，總諧波含量THD降至0.9%.由于閉環學習控制的輸出不僅與當前誤差相關，也與上一周期的控制輸出相關，真正起到了“學習過去經驗并根據當前誤差進行調節”的作用，從而獲得了較好的控制效果.

雖然ILC控制器有著較好的穩態性能，能夠精確地跟蹤期望波形，但是在其學習過程中，系統的動態性能表現得并不理想，這一點在開環學習中顯得尤為明顯(見圖5).即便是仿真效果較好的閉環學習方式也需要經過3-4個周波才能完成學習過程，在該過程中電壓有效值最低至211 V，THD含量最高達5.8%，具體見圖6.因此，在今后需要進一步研究如何改善迭代學習控制動態性能的方法.

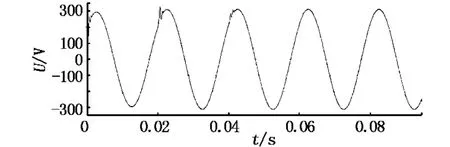
圖6 閉環學習ILC控制器的學習過程

在仿真過程中發現，采用PI型學習律的ILC控制器相對P型學習律的ILC控制器在控制效果上并無明顯提高，而PI型學習律相對P型學習律在學習軸上并無變化，只是在時間軸上加入了積分器.同時，積分器在頻域上僅能對低頻信號實現良好的無差調節效果，而高頻的交流軌跡和跟蹤誤差則很難調節.P型學習律的誤差曲線見圖7.

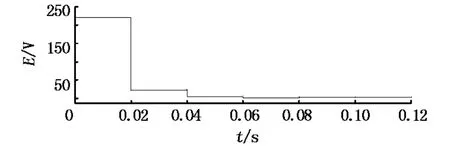
圖7 P型學習律的誤差曲線

另外，鑒于在數字控制器中微分器D采用較小的微分步長做除數會放大測量信號的誤差，從而造成系統失穩，因此較少采用PD型學習律.

4 結語

本文針對傳統PWM雙環控制逆變器在非線性負載工況下出現的輸出電壓波形畸變問題，應用迭代學習控制方法對其進行改善，仿真結果表明該方法是可行的，在學習過程結束后，逆變器的輸出波形得到了較大改善.同時，在周期性過程的迭代學習控制應用中，需要注意其不夠理想的動態性能.在今后的研究中可以將迭代學習控制與其他具有良好動態性能的控制方法相結合，以獲得既有良好動態性能又具有高精度跟蹤性能的控制器.

［1］龐慶，王震，占江山.基于重復學習控制的400 Hz逆變電源研究［J］.電力電子技術，2010，44(5):67-69.

［2］于少娟，齊向東，吳聚華.迭代學習控制理論及應用［M］.北京:機械工業出版社，2005:6-9.

［3］謝勝利，田森平，謝振東.迭代學習控制的理論與應用［M］.北京:科學出版社，2005:3-12.

［4］許建新，侯忠生.學習控制的現狀與展望［J］.自動化學報，2005，31(6):943-953.