基于提升小波的單歷元GPS變形監測信號的去噪*

陶庭 葉高飛 吳兆福

(合肥工業大學土木與水利工程學院，合肥230009)

基于提升小波的單歷元GPS變形監測信號的去噪*

陶庭 葉高飛 吳兆福

(合肥工業大學土木與水利工程學院，合肥230009)

介紹提升小波閾值收縮法去噪的基本原理和方法，利用該方法對含噪的GPS單歷元變形監測數據進行去噪，提取真實變形信息。實際數據處理結果表明，相比第一代小波，提升小波變換去噪效果更好，計算速度更快。

提升小波;變形監測;GPS;高頻噪聲;去噪

AbstractThe threshold shrinkage denoising method based on lifting wavelet transform is expatiated.Besides，the method is used to filter the noise from single epoch GPS deformation monitoring data and get the real deformation information.The experimental data processing results show that the advantage of lifting wavelet transform lies on better denoising effect and consuming shorter time than traditional wavelet transform.

Key words:lifting wavelet;deformation monitoring;GPS;high frequency noise;denoising

1 引言

GPS技術在各類變形監測中得到廣泛應用。通常，GPS變形觀測的作業方式有周期性的重復測量、固定連續GPS測站陣列與實時動態3種［1］。GPS實時動態變形監測采用的是RTK技術，即實時動態載波相位差分GPS測量，其定位方式屬于雙差相位觀測模型，常用于建筑物、橋梁監測。實時動態監測時基準站與監測站距離比較近，屬于短基線差分GPS測量，其中大多數誤差可以通過差分方法消除或減弱。而單歷元變形信息屬于高采樣頻率的數據源，受各種干擾信號的影響，解算得到的變形信息中會有大量高頻噪聲。因此要獲得準確的變形信號必須要對GPS變形坐標序列進行去噪。

文獻［2］提出的第二代小波變換是一種基于時域運算的信號分析方法，與第一代小波變換不同的是，它不依賴傅里葉變換，放棄了伸縮和平移條件，卻同樣可以獲得與經典小波變換相同的時頻特性，且可通過設計預測系數和提升系數，構造某種特性的第一代小波。提升小波降低了傳統的小波變換的計算復雜度，提高了去噪效率，且無需額外內存。

本文利用提升小波對GPS動態變形監測坐標序列數據進行去噪，提取真實的變形信息。試驗數據處理結果表明，該方法具有去噪效果好、計算速度快等優點。

2 基于提升小波的閾值去噪

2.1 提升小波

基于提升方案的小波變換稱為提升小波變換［3－5］。

設數據序列為λ={λ(k)，k∈Z}，基于提升方案的小波變換可以用以下3個步驟描述［4］:

1)分裂:將數據序列{λ(k)，k∈Z}分為奇樣本序列{λodd(k)，k∈Z}(λodd(k)表示奇樣本)和偶樣本序列{λeven(k)，k∈Z}(λeven(k)為偶樣本)。

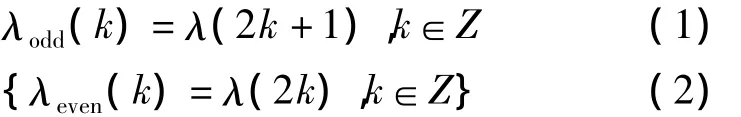
2)預測:dj(k)=λ(2k+1)－P(λ(2k))，k∈Z。P為預測算子，所得dj為小波系數。

3)更新:cj(k)=λ(2k)－U(dj(k))，k∈Z。U為更新算子，所得cj為尺度系數。

重復以上3個步驟就可以創建多分辨分解的多級變換。圖1表示的是提升算法的分解過程與重構過程。

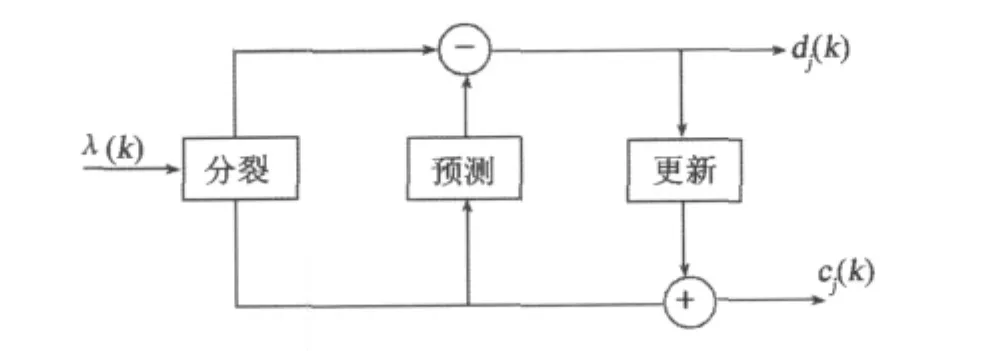
圖1 提升小波變換Fig.1Lifting wavelet transformation

2.2 基于提升小波的閾值收縮法去噪

小波閾值收縮法去噪的原理為［6］:由于小波變換具有很強的去數據相關性，小波變換后的信號能量主要集中小波域中在一些大的小波系數中;而噪聲的能量卻在小波變換后分散到各個小波域。經小波分解后的有用信號的小波系數幅值要明顯大于小波分解后噪聲的小波系數幅值。因此，可將幅值比較大的小波系數看作是有用信號，而將幅值比較小的小波系數當作噪聲。而采用閾值收縮法消噪就是保留用信號的小波系數而減小大部分噪聲的小波系數。

提升小波閾值收縮法去噪的基本步驟是:

1)先對含噪信號s做提升小波變換得到一組小波系數wj，k;

2)通過對wj，k進行閾值處理得出估計小波系數w^j，k使得w^j，k－wj，k盡可能小;閾值法分為軟閾值法與硬閾值法［6］。

軟閾值的算法如下:

該算法將信號分解后的小波系數與依公式所求的閾值λ進行比較，如果某點小波系數大于等于閾值，則該點小波系數收縮變成該點小波系數與閾值的差值;如果某點的小波系數小于閾值相反數，則該點的小波系數收縮為該點的小波系數與閾值的和;如果該點的小波系數的絕對值小于等于閾值，則該點的小波系數變為零。

硬閾值的算法如下:

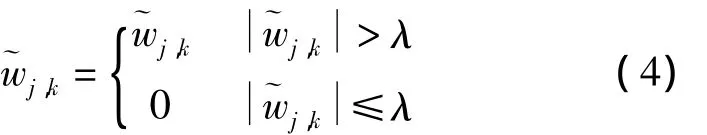
該算法同樣是將信號分解后的小波系數與依公式所求的閾值λ進行比較，如果某點的小波系數的絕對值大于等于閾值，則該點的小波系數保持不變;如果某點的小波系數的絕對值小于閾值，則該點的小波系數變為零。

3)根據收縮得到的小波系數~wj，k，利用提升小波對信號進行重構，得到的信號^s即為去噪之后的信號。

3 基于提升小波的單歷元GPS變形監測信號的去噪

3.1 數據來源

試驗地點選在某實驗樓頂，基準站設在地面穩定的觀測墩上固定不動。流動站天線設置在樓頂某細鋼筋上。由于風力等其他因素作用，鋼筋會發生位移。基準站與流動站周圍開闊，沒有反射物體，不會產生多路徑效應誤差。兩站之間距離只有100多米，屬于短基線差分GPS測量。其中的大多數誤差都可以通過差分方法消除或削弱，如衛星鐘差、接收機鐘差可以完全消除;而衛星軌道誤差、對流層延遲誤差、電離層延遲誤差等能得以很好地削弱。因此，觀測所得坐標序列的誤差主要為高頻噪聲。選用Leica GPS1200雙頻接收機，將采樣率設為1 Hz，衛星的截止高度角設為20°。

圖2是X方向含噪聲的4 000個歷元的GPS變形監測數據，從圖2中可以看出真實的變形信號受到噪聲的污染，要獲得準確的變形信息，必須對該信號進行去噪。

3.2 數據處理

分別采用提升小波與傳統小波對含噪信號進行閾值收縮法去噪。

首先選用第一代小波，采用閾值收縮法去噪，選用的小波基為具有正交緊支撐的Daubechies小波。選用db2小波，進行閾值收縮法消噪。去噪結果如圖3所示。

再利用提升db2小波對上述觀測值信號做小波分解及相關的閾值消噪處理。進行4層分解，利用閾值收縮法把分解得到的小波系數進行收縮處理，再利用收縮后的小波系數進行信號重構。圖4為提升小波去噪后得到的信號。

通過降噪處理，原始信號中的噪聲基本被濾除，得到的有用信息客觀地反映了原始信號的主要成分。現在采用去噪后的信噪比與均方根誤差來定量地分析兩種小波去噪效果。

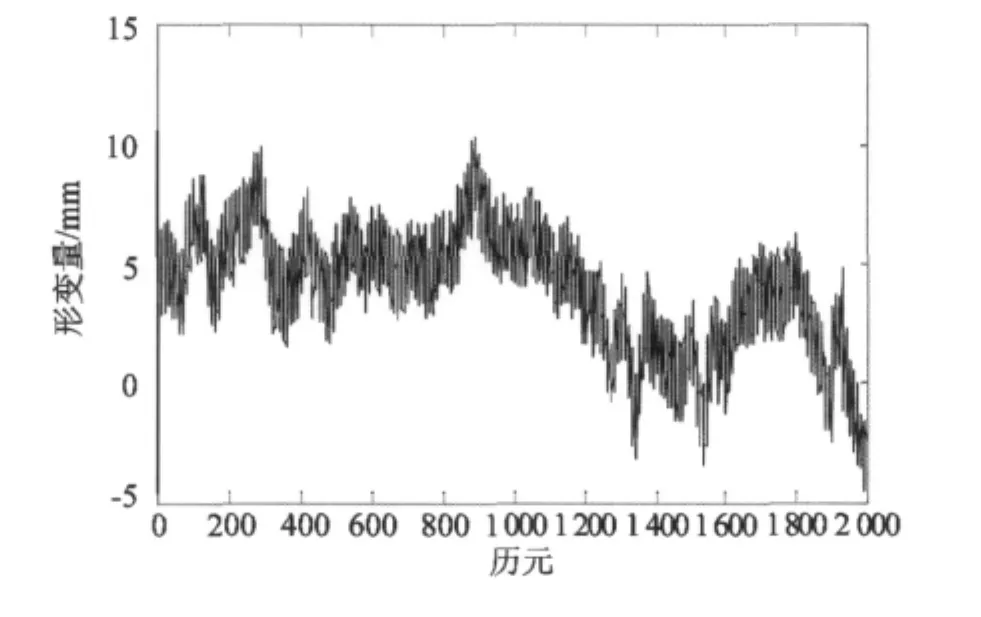
圖2 含噪聲的GPS單歷元變形監測信號Fig.2Nosing single epoch GPS deformation monitoring signal

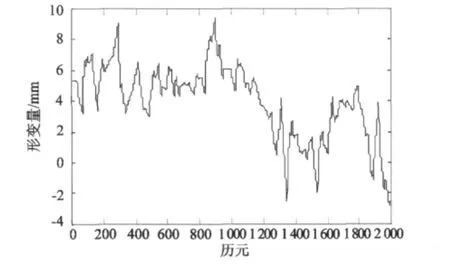
圖3 傳統小波去噪結果Fig.3Denoising results by using traditional wavelet

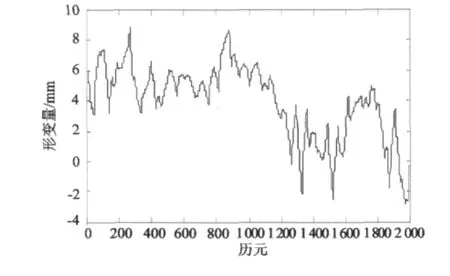
圖4 提升小波去噪結果Fig.4Denoising results by using lifting wavlet

信噪比定義為:

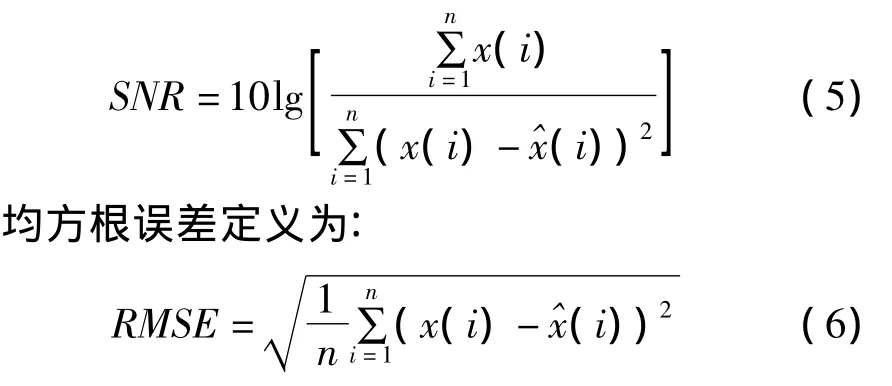
這里，x(i)為標準信號，^x(i))為消噪后得到的估計信號，n為原始信號的長度。

信號的信噪比越高，原始信號與估計信號的均方根誤差越小，表明估計信號就越接近于原始信號，去噪效果越好。兩種小波去噪后，其信噪比與均方根結果如表1所示。

表1 兩種方案去噪效果比較Tab.1Comparison between denoising results with the two different methods

在耗費時間方面，采用第一代小波所需的CPU時間為7.984 4 s，而采用第二代提升小波所耗費的CPU時間為7.515 6 s，說明第二代小波計算速度更快。

上述數據處理結果表明，提升小波及其傳統小波均能將含噪的變形信號中的高頻噪聲濾除，但提升小波濾波后的信號信噪比更大，原始信號與估計信號的均方根誤差更小，這說明相比第一代小波，提升小波的降噪效果更好。另外，提升小波的計算速度比傳統小波更快。

4 結語

單歷元GPS變形監測信號的去噪結果表明:利用提升小波能更好地對單歷元GPS變形監測信號進行去噪，有效提取真實變形信息;相比傳統小波其計算速度更快，這一點在處理海量數據時優勢明顯。

1戴吾蛟，等.GPS建筑物振動變形監測中的單歷元算法研究［J］.武漢大學學報(信息科學版)，2007，3(4):321－327.(Dai Wujiao，et al.Single epoch ambiguity resolution in structure monitoring using GPS［J］.Geomatics and Information Science of Wuhan University，2007，3(4):321－327)

2孫延奎.小波分析及其應用［M］.北京:機械工業出版社，2005.(Sun Yankui.Wavelet analysis and it’s application［M］.Beijing:China Machine Press，2005)

3Sweldens W.The lifiting scheme:A custom－design construction of biorthogonal wavelets［J］.App l Comput Harmon Anal.，1996，3:186－200.

4Sweldens W.The lifiting scheme:A construction of second generation wavelets［J］.SIAMJ Math Anal.，1997，29: 511－546.

5Daubech Ies I and Sweldensw.Factoring wavelet transforms into lifting steps［J］.J Fourier Anal Appl.，1998，4:247－269.

6Donoho D L.De-noising by soft threshold［J］.IEEE Trans.Info.Theory，1993，43:933－936.

DENOISING METHOD FOR SINGLE EPOCH GPS DEFORMATION MONITORING SIGNAL BASED ON LIFTING WAVELET

Tao Tingye，Gao Fei and Wu Zhaofu
(School of Civil and Hydraulic Engineering，Hefei University of Technology，Hefei230009)

P207

A

1671-5942(2011)03-0127-04

2010-11-21

國土環境與災害監測國家測繪局重點實驗室開放基金(LEDM2010B08);合肥工業大學博士學位專項基金(2010HGBZ0564)

陶庭葉，男，1980年生，講師、博士，主要研究方向為GNSS定位技術與變形監測.E－mail:czytty@163.com