高速永磁電機機組軸系振動研究

王天煜，王鳳翔，方 程

(1.沈陽工程學院 機械工程系，沈陽 110136;2.沈陽工業大學 電氣工程學院，沈陽 110870)

高速電機由于轉速高，體積小，功率密度大等優點，符合當前低碳經濟發展需要，已成為電機領域的研究熱點之一［1－3]。對于采用磁力軸承支承的高速電機轉速一般在30 000 r/min以上，在高速旋轉機械中，轉子振動逐漸成為制約電機正常運行的瓶頸。電機轉子振動的來源主要包括偏心產生的離心力和不平衡磁拉力。當這兩種激勵的頻率達到或接近轉子的固有頻率時，轉子的振動將會加劇產生共振。因此，預測電機的不平衡響應特性對于電機的高速可靠運行是非常有必要的。

對于電機不平衡響應的研究應考慮不平衡磁拉力UMP(Unbalanced Magnetic Pull)的影響。對于不平衡磁拉力的計算已逐步完善，曲鳳波［4]和姜培林［5]分別采用不同的方法得到了不平衡磁拉力的近似非線性計算式;文獻［6] 給出了UMP的非線性表達式，建立了電磁振動的非線性系統方程。本文采用有限元及Newmark積分法計算轉子在不平衡力作用下非線性響應，以額定轉速60 000 r/min高速電機樣機振動實驗驗證計算方法的正確性。通過機組振動實驗分析軸系振動產生的原因，提出減小振動的措施。

1 轉子不平衡力響應求解

作用在轉子上的合外力包括UMP和轉子質量偏心造成的不平衡離心力，則系統的運動方程為:

假設t+Δt時刻的速度和位移為:

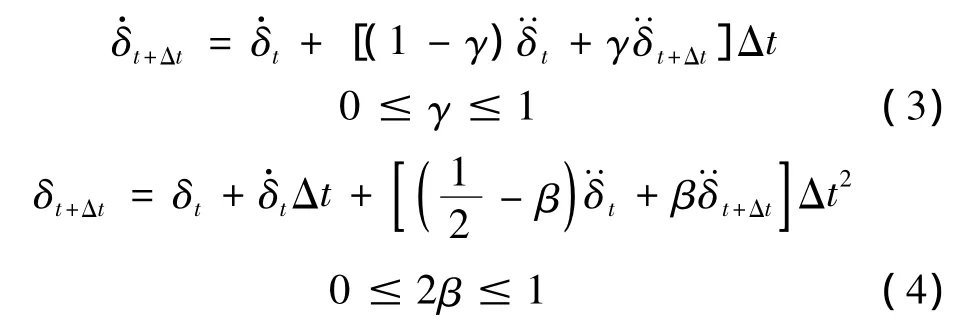
對式(2)～式(4)構成的方程組求解，即可得t+ Δt時刻的位移 δ、速度和加速度。Δt是

t+Δt時間步，γ和 β是 Newmark參數，選擇 γ =0.5，β =0.25，保證積分過程無條件穩定［7]。

2 單轉子不平衡響應分析

本文研究的高速電機轉子采用磁力軸承支承，能夠實現振動的主動控制，且磁力軸承轉子系統為剛性轉子，正常運行情況下轉子的質量偏心量較小。本文計算不同轉速下轉子不平衡力對轉子系統振動的影響。

2.1 10 000 r/min轉子振動響應分析

計算n=10 000 r/min轉子只受離心力(不考慮UMP)作用下的振動響應，圖1為轉子在y方向振動響應及頻譜。從圖1中可知，只受離心力作用下轉子產生基頻(167 Hz)振動。

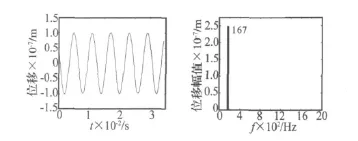
圖1 n=10 000 r/min時離心力作用下的振動響應及頻譜Fig.1 Vibration response and spectrum acted by centrifugal force，n=10 000 r/min

圖2 為轉子只受UMP作用下y方向的振動響應及頻譜。UMP產生的諧波次數與定轉子槽數、電機的極數有關。高速電機轉子為2極，對于兩極電機由于偏心的存在，其UMP在y方向上存在直流分量［8]，且使轉子振動位移增大(見圖2)。高速電機轉子沒有齒槽，定子12槽，UMP含有齒槽諧波且諧波占有很大的比重，必須考慮高頻諧波對轉子振動的影響。從圖2中可以看出，UMP中的10次諧波(1 667 Hz)與轉子的1階彎曲模態的固有頻率很接近(見圖6)，因此引發轉子的彎曲共振。UMP的2次諧波成分，由于幅值比較大，頻率比較低，因此引起轉子2倍頻的振動也比較明顯。轉子雖然受到12次諧波作用，但由于其激振頻率遠離轉子固有頻率且頻率較高，因此其產生的振動較小。

圖2 n=10 000 r/min時UMP作用下的振動響應及頻譜Fig.2 Vibration response and spectrum of rotor acted by UMP，n=10 000 r/min

電機實際運行時，轉子受到UMP和質量偏心離心力的共同作用。圖3為轉子在UMP和質量偏心離心力共同作用下y方向的振動響應和頻譜圖。由頻譜圖可以看出，質量偏心離心力產生的基頻振動是轉子振動的主要來源，其次是UMP產生的10次諧波和2次諧波，考慮UMP后振動有所增加。

2.2 60 000 r/min轉子振動響應分析

圖4為n=60 000 r/min時轉子在UMP和質量偏心離心力共同作用下y方向的振動響應及頻譜圖。轉速增加后，質量偏心離心力是增加的，但其響應是減小的［9]。而UMP大小不變，但頻率卻是隨轉速增加而增大的，且都是高頻成分，所以隨著轉速的上升，UMP的2倍頻及高次諧波振動將迅速減弱，所以轉速越高UMP的作用越小。

驅動層介于系統層和硬件設備之間，提供應用程序訪問硬件設備資源的接口，同時也為存儲軟件提供了基礎環境和接口。linux系統將設備分為3類：字符設備、塊設備、網絡設備。考慮到安全存儲的硬件加解密設備與塊設備、網絡設備特性的差異，而與面向流的字符設備類似，驅動層在采用字符設備的基礎上提供相應的庫文件供應用程序實現加解密功能[15]。

2.3 仿真計算與實驗結果比較

離心力作用下不同激振頻率仿真計算的頻譜見圖5。計算轉子頻段為［105 Hz，2 000 Hz] 。圖6為轉子激振實驗得到的轉子振動模態及固有頻率。仿真計算表明在1 668 Hz出現共振，這與轉子激振實驗的1階彎曲模態固有頻率相一致［10]，驗證了仿真計算的正確性。

3 機組振動實驗

高速永磁電機機組由兩臺2極3相額定功率75 kW、額定轉速為60 000 r/min的高速永磁同步電機用聯軸器耦聯而成，其中一臺電機由變頻電源供電作電動機，另一臺作發電機，電動機、發電機定子均為環形繞組，定子內徑66 mm，轉子外徑64 mm，永磁體長度135 mm，定子齒數分別為12槽和24槽。

機組振動實驗分別利用兩臺電機磁力軸承的渦流傳感器測量轉子的動態特性;由兩對壓電式加速度傳感器監測兩臺電機機體的振動特性。圖7、圖8為高速電機實驗系統及機組。

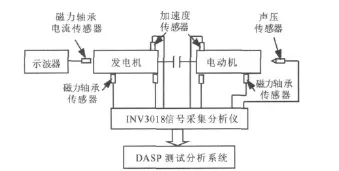
圖7 電機振動及噪聲測試系統Fig.7 Test system of noise and vibration of machine

圖8 高速電機機組Fig.8 High-speed motor unit

3.1 軸系軸心軌跡分析

圖9 為軸系中發電機靠近聯軸器端不同轉速下的軸心軌跡。圖9(a)為轉子升速到15 000 r/min軸心軌跡，是以工頻為主的橢圓形軌跡。隨著轉速增加，當轉速達到30 000 r/min時，軸心軌跡如圖9(b)，此時除了工頻以外，出現了另外一個非同頻振動頻率，導致系統偏離原先穩定的平衡點，軸系出現渦動現象。當轉速繼續增加到33 024 r/min(圖9(c))，渦動軌跡亦繼續擴大引起強烈振動。這時不平衡量稍有增加或稍有擾動，系統就會失穩。出現線性失穩之后，系統會進入新的非線性平衡點(圖9(d))，轉速有所降低。繼續增速系統出現混沌狀態(圖9(e))。圖9(f)為發電機末端即遠離聯軸器端軸心軌跡，軸心軌跡呈“8”字形，說明機組兩轉子存在不對中現象。

3.2 軸系振動頻譜分析

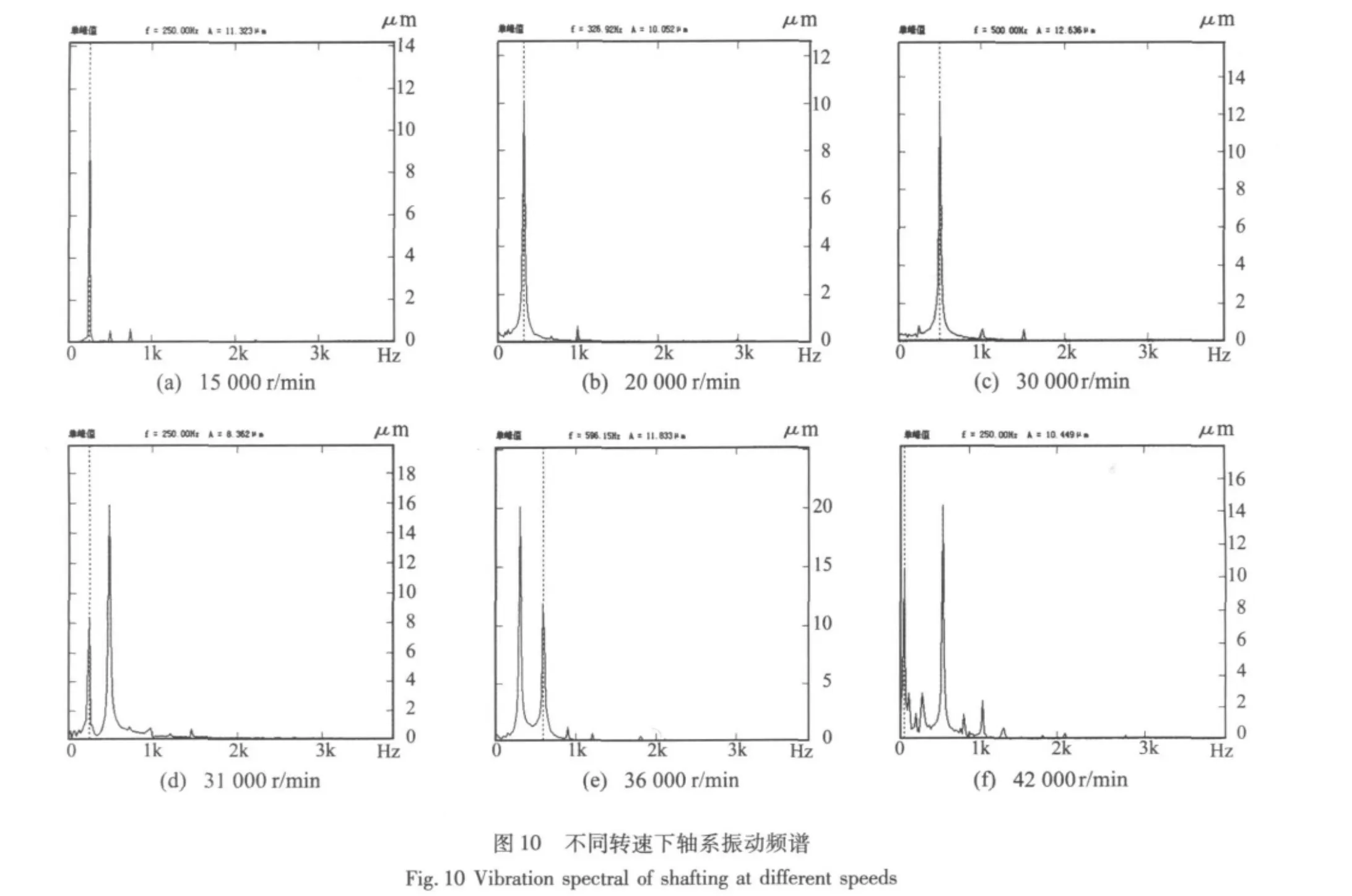
轉速譜陣圖是轉子振動特性曲線中最基本的分析曲線，是判斷旋轉機器故障的最常用方法。圖10為不同轉速下軸系振動頻譜。轉速為15 000 r/min時(圖10(a))，轉子主要為由質量不平衡力引起的基頻振動，其次為2倍、3陪頻分量。軸系不對中及轉子與定子氣隙不均勻均能誘發較大的2倍頻振動，氣隙不均勻誘發的2倍頻振動隨勵磁電流增大而增大。轉速為20 000 r/min時，軸系主要為基頻和3倍頻振動(圖10(b))，即隨著轉速的提高電磁力的作用減小而聯軸器不對中產生的振動略有增加。轉速升到30 000 r/min時開始出現半頻渦動(圖10(c))，隨著轉速的升高，半頻渦動幅值增大(圖10(d))，出現半頻振蕩(圖10(e))，轉速繼續升高，振動頻譜成分更復雜，出現分數倍頻的非線性振動，此時半頻振動幅值超過基頻振動幅值。

對于軸系出現的半速渦動的非線性振動現象，分析可能的原因:① 磁力軸承支承的非線性剛度;②連接兩電機的膜片聯軸器的內摩擦力。根據對軸系固有頻率的計算，當軸系轉速達到30 000 r/min時，軸系為柔性轉子，其1/2(250 Hz)階次諧波振動與軸系第4階固有頻率(247.5Hz)接近，轉子的自激振動轉化為1/2階次諧波共振，并且振動頻率始終等于固有頻率，不隨轉速變化而變化，這種進動將在一個轉速范圍內保持著，其振動幅值超過基頻幅值。

根據振動分析結果提出如下改進措施:可通過改變聯軸器結構尺寸即改變其徑向剛度，以減小內摩擦力，或選擇其它柔性聯軸器，以消減或排除這種自激振動。另外，徑向磁力軸承的承載能力不足，在外部擾動力作用下會限制磁力軸承系統性能的提高［11]，針對轉子的非線性強干擾力、軸系轉子不對中等問題，在控制器設計過程中，可以通過加大控制器剛度解決。即在低速下使用高剛度控制器，當電動機轉子運行到一定轉速，電動機干擾力對轉子運行影響下降時，將控制器切換到一個低剛度的控制器。此時，轉子系統的剛性臨界轉速將顯著下降，并且已經落到轉子同步頻率之下，即轉子已經實現了超越剛性臨界轉速運行，可以繼續穩定地升速。

3.3 機座振動分析

轉速33 000 r/min時對定子齒數z1=12的電動機進行機座振動測試。電機正常工作時離心力使轉子產生與電源基波頻率相同基頻的振動，徑向電磁力波由二倍頻及定、轉子齒槽引起的一系列高頻諧波組成，轉子靜、動偏心及電源諧波等因素同樣對振動產生很大影響。徑向力波的主要頻率成分組成如下［12]:

(1)轉子旋轉諧波頻率:f=2kpfr=2×k×1×550=1 100，2 200，…，Hz，k=1，2，3，…。

(2)定子齒槽諧波頻率:f=k1z1fr=k1×12×550=6 600，13 200，…，Hz，k1=1，2，3，…。

(3)轉子不對稱諧波相互作用頻率:f=jfr/p=j×550=550，1 100，…，Hz，j=1，2，3，…(j為轉子不對稱階數，j=1為轉子動偏心)。

(4)定子不對稱諧波相互作用頻率:f=2bfr=2×b ×550=1 100，2 200，…，Hz，b=1，2，3，…。

(5)定、轉子不對稱諧波相互作用頻率:

f=jfr/p±2bfr=(j±2b)×550=550，1 100，1 650，2 200，…，Hz，j=1，2，3，…，b=1，2，3…。

圖11為33 000 r/min負載下機座振動頻譜圖，測量位置為前后軸承處的水平和垂直方向。加速度頻譜中最高的五個峰值依次為:550 Hz、5 500 Hz、3 300 Hz、1 100 Hz和6 050 Hz。由圖11可知，電機的振動主要為離心力產生基頻振動及由于轉子動偏心產生的10倍頻的振動;其次是2倍頻的振動，還有動偏心及定、轉子不對稱引起的6倍頻、11倍頻的振動。由于轉子無槽，沒有轉子齒槽諧波，定子齒槽諧波的影響也較小。這與仿真結果(見圖3)是一致的。

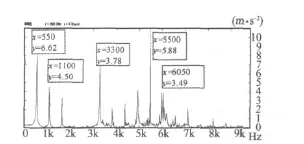
圖11 轉速33 000r/min負載時機座振動加速度頻譜Fig.11 Vibration acceleration spectrum of base at rated 33 000 r/min and at load

4 結論

用有限元方法及Newmark積分法計算轉子在機械、電磁等不平衡力作用下的振動響應。研究表明，2極電機UMP由2倍頻分量和一系列的高頻諧波分量組成。轉子轉速提高，質量偏心引起的轉子基頻振動占主要成分，UMP作用下產生的2倍頻和高頻諧波振動減弱;高速電機機組軸系的振動主要為由質量不平衡力引起的基頻振動，其次為2倍、3陪頻分量振動。機座的振動主要為基頻振動及由于UMP產生的10倍頻振動，其次是2倍頻振動。

［1] 周 強，劉 闖，朱學忠，等.超高速開關磁阻電動機設計［J] .中國電機工程學報，2009，29(9):87－92.

［2] 王鳳翔.高速電機的設計特點及相關技術研究［J] .沈陽工業大學學報，2006，28(3):258－264.

［3] Pang Y，Zhu Z Q，Howe D.Optimal split ratio for permanent magnet brushless machines［C] .Beijing:ICEMS’2003，I:128－ 131.

［4] 曲鳳波，孫玉田，曲大莊.水輪發電機的不平衡磁拉力［J] .大電機技術，1997，4:1－3.

［5] 姜培林，虞 烈.電機不平衡磁拉力及其剛度的計算［J] .大電機技術，1998，4:32－34.

［6] 姚大坤，鄒經湘，黃文虎.水輪發電機轉子偏心引起的非線性電磁振動［J] .應用力學學報，2006，23(3):334－337.

［7] Guo D，Chu F，Chen D.The unbalanced magnetic pull and its effects on vibration in a three-phase generator with eccentric rotor［J] .Journal of Sound and Vibration，2002，254(2):297－312.

［8] 方 程.高速永磁電機轉子特性分析及結構優化設計［D] .沈陽:沈陽工業大學碩士論文，2010.

［9] 東北大學，北京科技大學編.工程力學(運動學和動力學)［M] .北京:高等教育出版社，2008.

［10] 王天煜，王鳳翔，方 程.高速電機轉子臨界轉速計算與振動模態分析［J] .遼寧工程技術大學學報，2009，28(5):805－808.

［11] 張 剴，戴興建，張小章.強非線性條件下的磁軸承高速電動機［J] .機械工程學報，2007，43(8):202－206.

［12] 陳永校，諸自強，應善成.電機噪聲的分析和控制［M] .杭州:浙江大學出版社，1987.