基于二階段抽樣的雙重抽樣框估計量設計

賀建風

（仲愷農業工程學院 統計系，廣州 510225）

0 引言

傳統抽樣調查設計及其估計理論一般基于單一抽樣框的假定。然而，隨著社會經濟的飛速發展，城市化進程的推進與產業政策的轉移使得人口流動與生產單位轉移變得比以往任何時期都要頻繁，很難建立覆蓋所有目標單位的單一抽樣框，有時即使可以建成，建設費用也一定是高昂的，或者需要很長的時間才能完成，建成后還得耗費大量資源對其進行不斷地更新與維護，這不符合抽樣調查成本低、時效性強的原則。有一種方法可以彌補單一抽樣框覆蓋不完全問題，那就是采用雙重抽樣框（即兩個相互獨立的抽樣框），使他們聯合起來能夠完全覆蓋目標總體，當然這些抽樣框應該是現有的資料，或者能夠輕易構建起來，使提高調查精度的同時還可以節約調查的固定成本。

國外對于雙重抽樣框的理論研究起源于上世紀60年代。Hartley(1962，1974)對雙重抽樣框的估計問題進行了開創性研究[1]，隨后 Fuller and Burmeister(1972)，Bankier(1986)，Kalton and Anderson(1986)等人在此基礎上對雙重抽樣框的估計問題進行了拓展[2][3]，但是這些研究僅局限于單一階段抽樣，對于在雙重抽樣框抽樣情形下的二階段抽樣估計量研究的甚少，其中Casady,Snowden,and Sirken（1981）將Hartley 提出的基于雙重抽樣框的估計方法應用于電話名錄框與區域框組合抽樣設計的分層多階段抽樣[4]，B.C.Saxena,P.Narain,A.K.Srivastava（1984）探討了雙重抽樣框下的二階段抽樣估計問題，但是只考慮了次級抽樣單元在各域的單位調查成本相同的情形[5]。在國內，由于行政分級的政治模式，多階段抽樣調查成為實際中應用較廣泛的一種調查手段（尤其是政府調查項目）。國內理論界對于多階段抽樣的研究僅局限于單一抽樣框的前提，對于雙重抽樣框的情形未曾涉及。基于此，本文擬引進國外相對豐富的雙重抽樣框估計理論，研究國內目前流行的多階段抽樣調查，將多階段抽樣擴展到雙重抽樣框的情形，以求彌補國內在這一領域的空缺。為了分析問題的簡便及計算的簡單可行，本文僅對雙重抽樣框下的二階段抽樣調查進行研究，對于更多階段的抽樣調查情形可以按照本文的思路進行推廣。

1 符號及含義

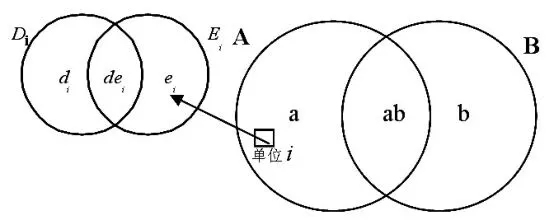
圖1 雙重抽樣框的一般結構

在二階段的抽樣中，假定每個階段都面臨著從雙重框中抽選調查單元。設第一階段抽樣有兩個存在相互重疊部分的抽樣框A與B共同組成目標總體，并記NA與NB分別為抽樣框A與B中的總體單位個數，nA與nB為獨立取自抽樣框A與B的樣本數。從總體中抽取的初級抽樣單元能夠被分入三個子域（見圖1），即域a，域b和域ab。

域a：包含來自于抽樣框A而不在抽樣框B中的總體單位，記Na為總體單元個數；

域b：包含來自于抽樣框B而不在抽樣框A中的總體單位，記Nb為總體單元個數；

域ab：包含來自于抽樣框A與B公共部分的總體單位，記Nab為總體單元個數。

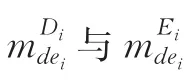
2 總體總值估計量

Hartley's(1962)提出簡單隨機抽樣情形下的總體總量事后分層估計量：

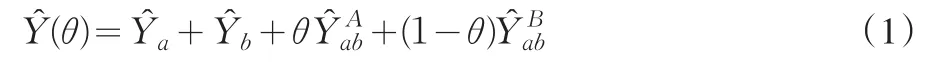
其中是域a的總體總值估計量，是域b的總體總值估計量，是域ab中來自A抽樣框的總體總值估計量，是域ab中來自B抽樣框的總體總值估計量，θ為抽樣權重系數，且0≤θ≤1。

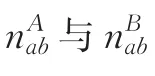
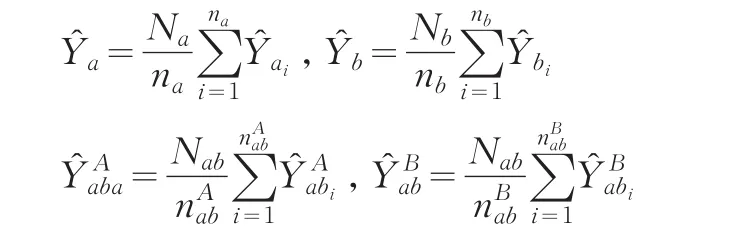
類似（1）式，第i個初級抽樣單元的總體總量事后分層估計量為：

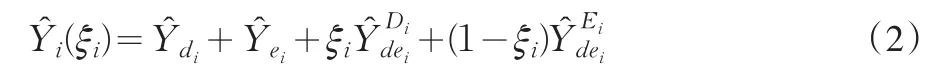
將（2）式代入第一階抽樣下各子域的總體總值估計量公式中，再代入式（1）可得：

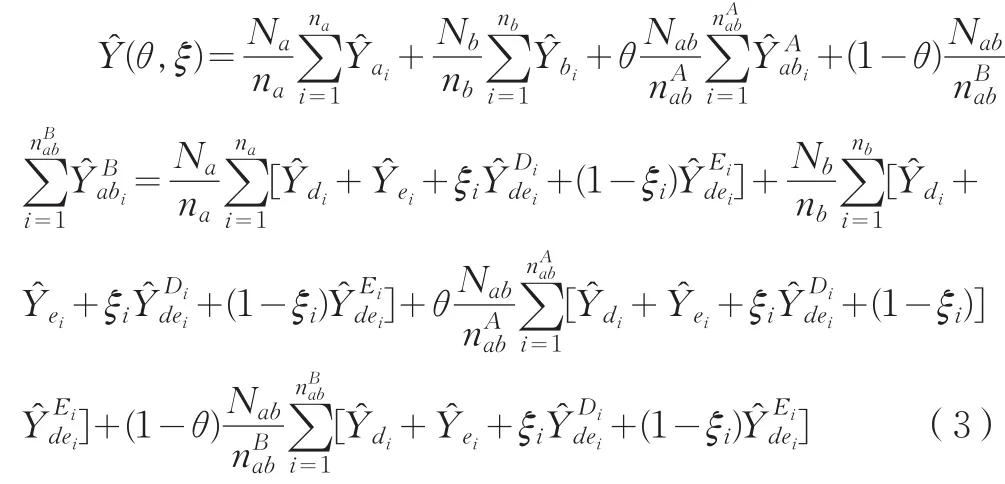
3 總值估計量方差和方差的無偏估計

由于從兩個抽樣框選取樣本是相互獨立的，所以來自A抽樣框的統計量與來自B抽樣框的統計量之間的協方差為0，即：

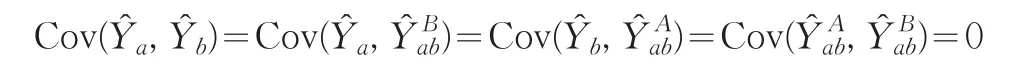
所以（1）式中總體總值估計量的方差可以表示為：

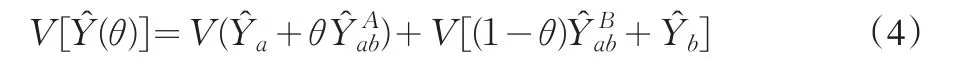
對于每個抽樣框的兩個子域進行事后分層，估計量的方差接近于：

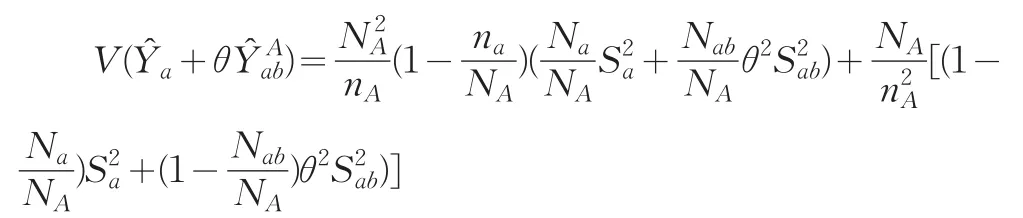
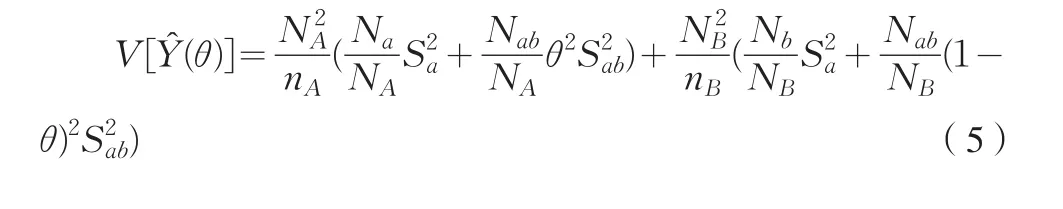
根據式（5）估計量(θ)的方差，利用二階段抽樣的估計量方差公式可以推出（3）式估計量(θ,ξ)的方差為：

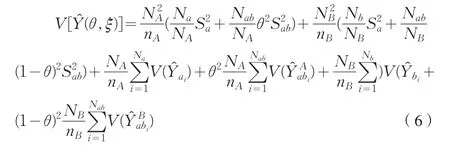
接下來，可以給出估計量方差的無偏估計，其具體形式如（8）式：

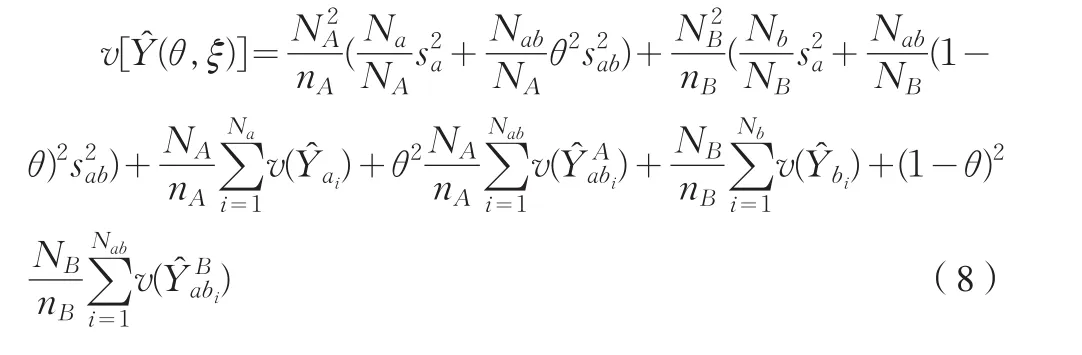
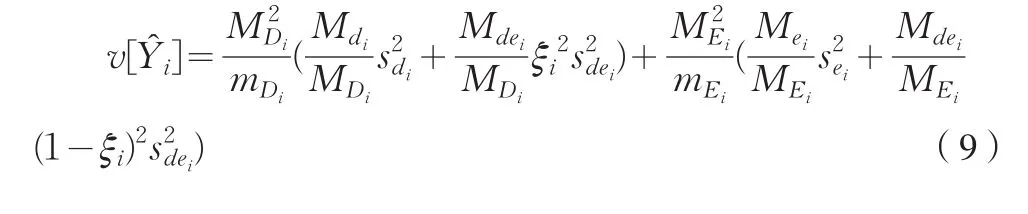
4 結束語

本文打破了傳統抽樣調查僅基于單一抽樣框分析的束縛，引進了在實際中成本更低廉、覆蓋面更廣的多重抽樣框調查新思路；針對雙重抽樣框下的二階段抽樣估計理論進行了研究，給出了總體總值估計量及其估計量方差，并給出了方差的無偏估計。本文的重要意義在于為二階段抽樣中采用雙重抽樣框提供理論支持。

本文的研究展望有如下幾點：其一，本文的研究僅基于所有階段以及各抽樣框的調查均為簡單隨機抽樣的情形，更進一步的研究需要將這一估計方法拓展到一般類型抽樣調查的場合；其二，對于多重抽樣框以及多階段的情形本文并未展開分析，感興趣的讀者可以在本文的基礎上進行拓展，但估計量的計算將更為繁瑣；其三，本文考慮的是二個階段均為雙重抽樣框的情形，并且假定所有雙重抽樣框的結構均為圖1所示，對于某階段為單一抽樣框以及雙重抽樣框的結構為完全重疊或某抽樣框包含另一個的情形而言，其估計量的計算比本文更簡單。限于篇幅，這里不再贅述。

[1]Hartley H.O.Multiple Frame Surveys[C].In Proceedings of the Social Statistical Section,ASA,1962.

[2]Hartley,H.O.Multiple-Frame Methodology and Selected Applications[J].Sankhya,Ser.C,1974，（36）.

[3]Fuller,W.A.,Burmeister,L.F.Estimators for Samples Selected from Two Overlapping Frames[C].In Proceedings of the Social Statistics Section,American Statistical Association,1972.

[4]Casady,R.,Snowden,C.,Sirken,M.A Study of Dual Frame Estimators for the National Health Interview Survey[C].Proceeding of the Survey Research Methods Section,American Statistical Association,1981.

[5]B.C.Saxena,P.Narain,A.K.Srivastava.Multiple Frame Surveys in Two Stage Sampling[J].The Indian Journal of Statistics，1984，(4).