客運專線32 m預制簡支箱梁靜載試驗研究

張洪雨，盧文良，賈 桐

(北京交通大學 土木建筑工程學院，北京 100044)

預制整孔簡支箱梁以抗扭剛度大、受力明確、建設速度快、質量有保證、建成后的橋梁維養工作量小以及低噪聲等優勢，在鐵路客運專線中被廣泛采用。箱梁質量直接影響整條線路的狀態，為預防施工事故，保證橋梁建成后正常運行，應采取科學合理的措施對箱梁質量加以控制。對實橋進行動靜載試驗是檢驗橋梁性能的有效評定手段［1-3］，在眾多控制箱梁質量的措施中，靜載試驗是檢驗箱梁性能的主要方法，通過靜載試驗可檢驗箱梁的剛度和抗裂性是否滿足設計要求。制梁場在箱梁生產初期和生產過程中，應根據相關規范的要求對箱梁進行靜載試驗，以確保箱梁的質量安全可靠［4-5］。靜載試驗可采用自平衡或加載框架方式對梁進行加載，本文針對目前廣泛采用的自平衡加載方式進行研究。

1 靜載試驗方案

試驗梁為32 m預應力混凝土簡支箱梁(通橋(2008)2322A-Ⅱ)，梁長32.6 m，支座中心距縱向(計算跨徑)31.5 m、橫向4.5 m，梁高3.05 m，頂板寬12 m，底板寬5.5 m，單片箱梁質量900 t。試驗采用自平衡加載方式，加載過程中對箱梁分等級多點同步加載，測試箱梁在荷載作用下的撓度值，并觀測梁體有無裂縫出現及裂縫的擴展情況，通過對試驗數據分析處理，根據規范及設計要求判斷梁體質量是否安全可靠。

1.1 試驗測試設備

1)試驗臺座

靜載試驗臺座由2片鋼縱梁、2片上枕梁、2片下枕梁及4組拉桿組成。鋼縱梁與上枕梁由多組耳板連接，上下枕梁由4組拉桿相連。每組拉桿由6根 φ32的精軋螺紋鋼組成。試驗梁置于上下枕梁之間，通過油泵和千斤頂對試驗梁進行加載試驗。試驗臺座應能確保試驗梁跨度、支承方式和加載狀態符合試驗加載要求，且具有足夠的強度、剛度和穩定性。現場試驗臺座如圖1所示。

圖1 試驗臺座

2)其他設備

除試驗臺座外，試驗還需用千斤頂、油泵、標準油壓表或壓力傳感器等加力設備和計量儀器。試驗所用計量設備、儀器、儀表、鋼卷尺等均需經法定計量檢定部門檢定合格，且在有效期內使用。

1.2 試驗加載測試

根據規范，32 m箱梁采用五集中力四分點加載方式，跨中設一集中荷載，其余在其左右對稱布置，各點縱向間距為4 m，如圖2所示。加載分兩個循環進行，以加載系數K表示加載等級，加載系數K是加載試驗中梁體跨中承受的彎矩與設計彎矩之比，通過梁體所受彎矩反算得到加載荷載。試驗準備工作結束后梁體承受的荷載狀態為初始狀態;基數級下梁體跨中承受的彎矩指梁體質量與二期恒載質量對跨中彎矩之和。

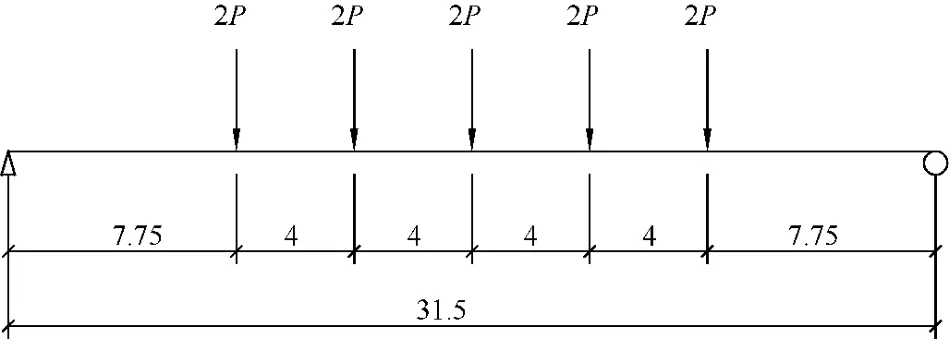
圖2 加載圖式(單位:m)

第一循環最大加載荷載為設計荷載，第一加載循環兼有試壓作用，消除試驗中加載設備、梁體及支座等相互之間潛在的不密實因素，第二加載循環在第一加載循環基礎上進行，最大加載荷載為1.20倍設計荷載，是檢驗梁體抗裂性的主要過程。第一與第二加載循環都應嚴格按照規范及設計要求進行，其結果均為梁體質量判定的依據。以加載系數K表示加載等級的第一與第二加載循環程序見表1。

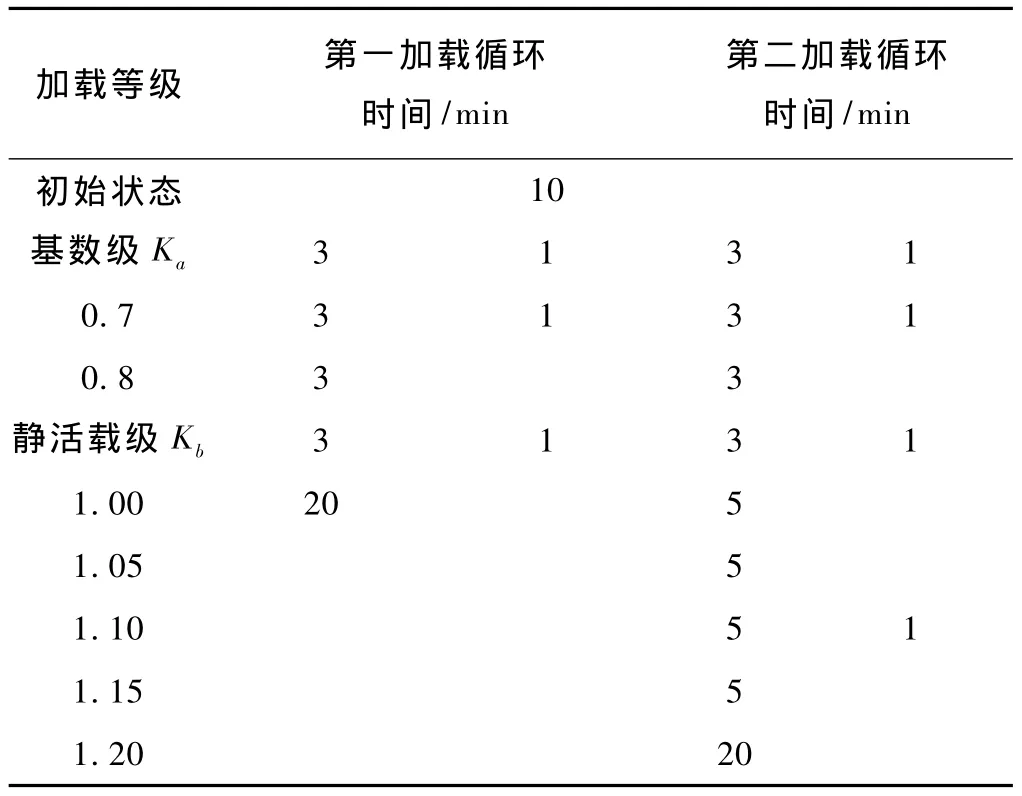
表1 加載程序

每級加載后均應仔細檢查梁體下緣和梁底有無裂縫出現。如發現裂縫，應標注裂縫位置，量測裂縫寬度并注明荷載等級。每級加載后均應測量梁體跨中和各支座中心截面兩側豎向位移變化，以同一截面的兩側平均值作為相應截面的豎向位移量或支點沉降量。跨中截面豎向位移量減去支座沉降影響量即為該級荷載下的實測撓度值。

1.3 評定標準

1)梁體剛度

通過實測靜活載撓度f實測大小判斷梁體剛度是否合格，合格評定標準為

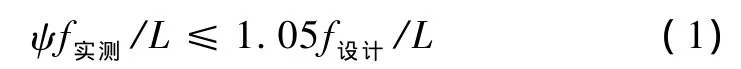
式中，L為箱梁的計算跨徑，為31.5 m;ψ為等效荷載加載撓度修正系數，為0.998 7。

2)梁體抗裂性

在K為1.20加載等級下持荷20 min，梁體下翼緣側、底面未發現受力裂縫或下翼緣側面的受力裂縫未延伸至梁底邊，則梁體抗裂性合格。

2 靜載試驗結果分析

本文收集了12片32 m預制簡支箱梁靜載試驗的數據，同時針對各片梁的加載情況，用Midas軟件進行了撓度計算。通過試驗值與理論計算值對比分析，對試驗梁的整體狀況做出評價。

2.1 實測數據及分析

按照前述試驗方法對12片梁進行靜載試驗，撓度實測值見表2，表中Ka代表基數級，Kb代表靜活載級，靜活載(即ZK活載)撓度值為靜活載級撓度值減去基數級撓度值，撓度—荷載曲線如圖3所示。對試驗靜活載撓度值進行統計分析，平均值為4.81 mm，撓跨比為1/6 549，標準差為0.369，變異系數為0.077。靜活載跨中撓度設計值為5.98 mm，撓跨比為1/5 268。

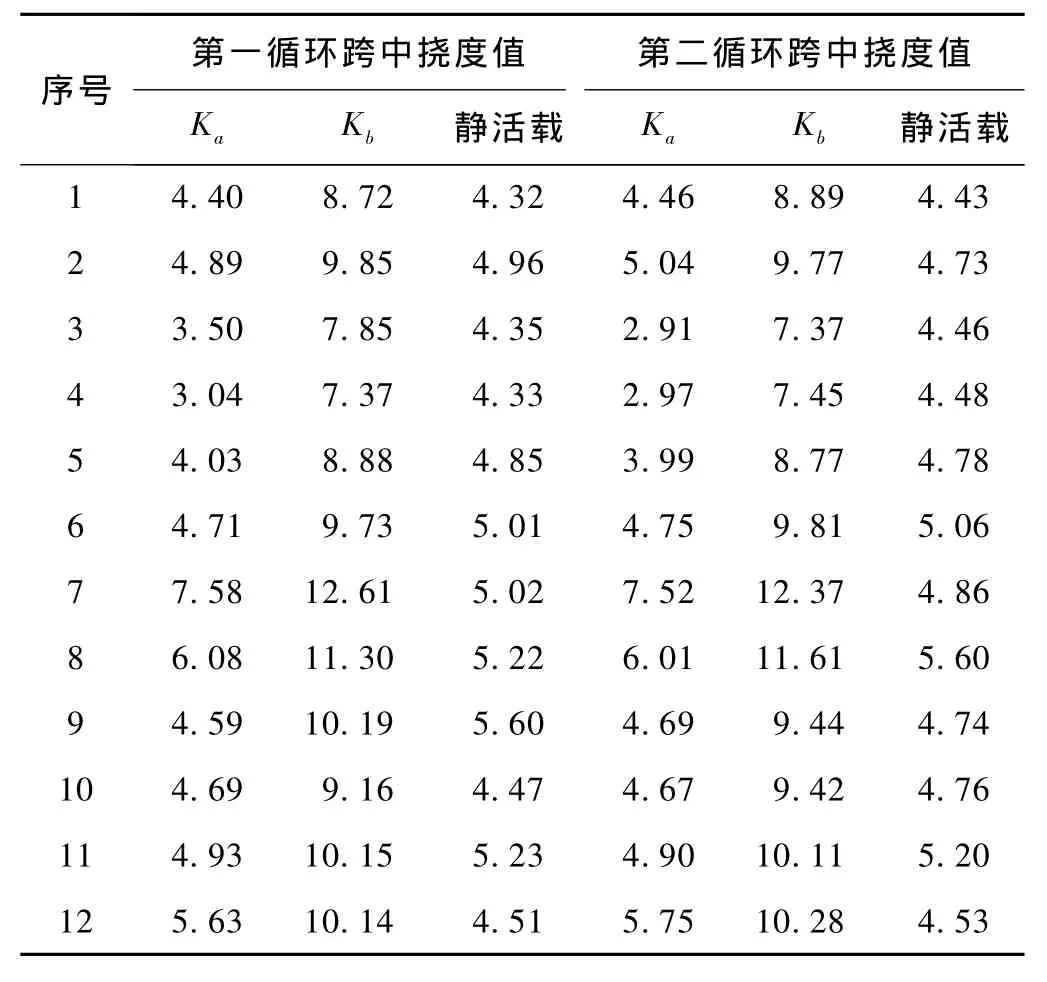
表2 實測跨中撓度值 mm

由圖3可以看出各片梁撓度值與荷載基本上均為線性關系，說明梁體發生的變形為彈性變形。不同梁在同一級荷載下撓度值變化幅度稍大，是由于本文12片32 m簡支箱梁靜載試驗的數據取自不同的梁場，梁體在彈性模量、二期恒載和試驗設備等方面有所不同。靜活載撓度值相差不大，彈性模量差異是引起同一荷載下各梁撓度值不同的主要原因。試驗結果均滿足設計要求，梁場在生產技術和產品質量方面滿足要求。試驗梁第二加載循環，在Kb為1.20加載等級時對應圖3第二循環中最后一點，此時持荷20 min，試驗梁下翼緣底部邊角及梁底面均未發現受力裂縫，表明梁體抗裂性滿足規范及設計要求。由圖3還可以看出，1.20倍設計荷載時梁體撓度值與荷載基本保持線性關系，說明梁體依舊處在彈性變形階段，梁體質量安全可靠。

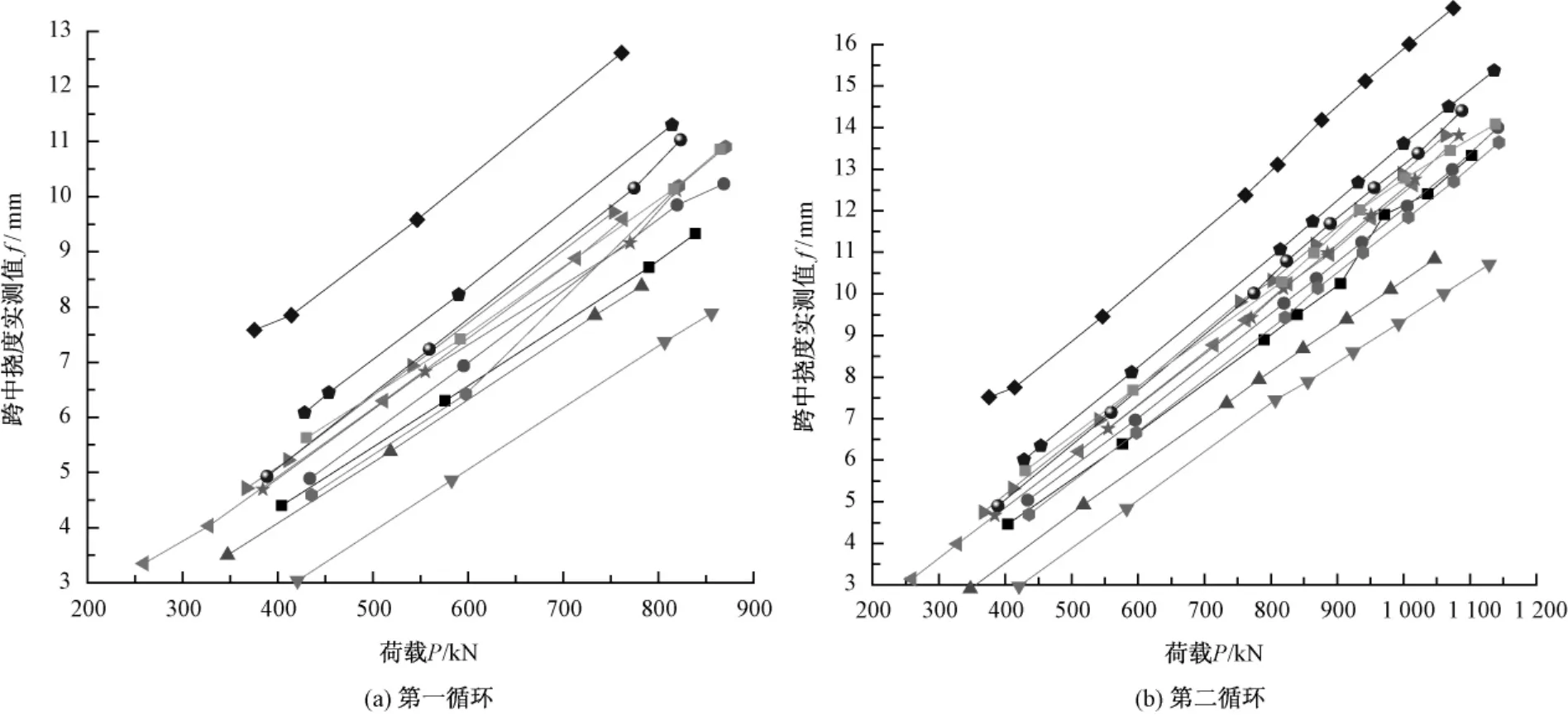
圖3 試驗梁跨中f—P關系曲線

2.2 理論計算

根據箱梁設計及試驗參數建立Midas有限元計算模型，如圖4所示，按照靜載試驗加載圖式計算的箱梁撓曲示意圖如圖5所示。采用Midas對各試驗梁進行計算，得到各片梁在各個加載級別下的撓度值，同時采用傳統梁理論［6］計算梁體跨中撓度值，計算結果見表3。由表3可以看出，不同梁體在靜活載下撓度值大體一致，按傳統梁理論計算靜活載跨中撓度值約為4.73 mm，撓跨比為1/6 660;有限元法計算靜活載跨中撓度值約為4.97 mm，撓跨比為1/6 338。

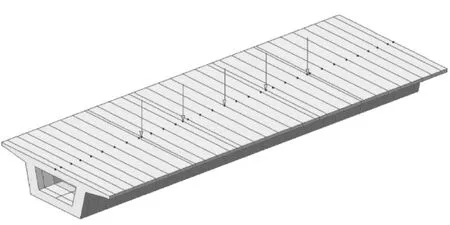
圖4 箱梁有限元模型

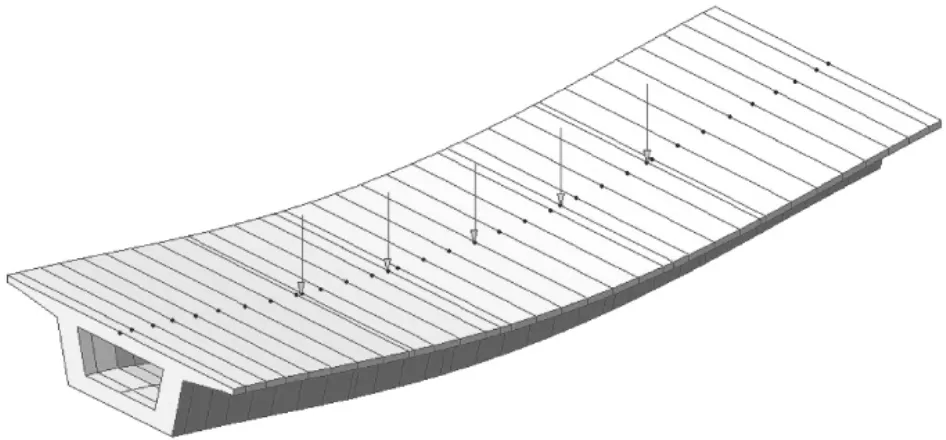
圖5 箱梁加載后撓曲示意

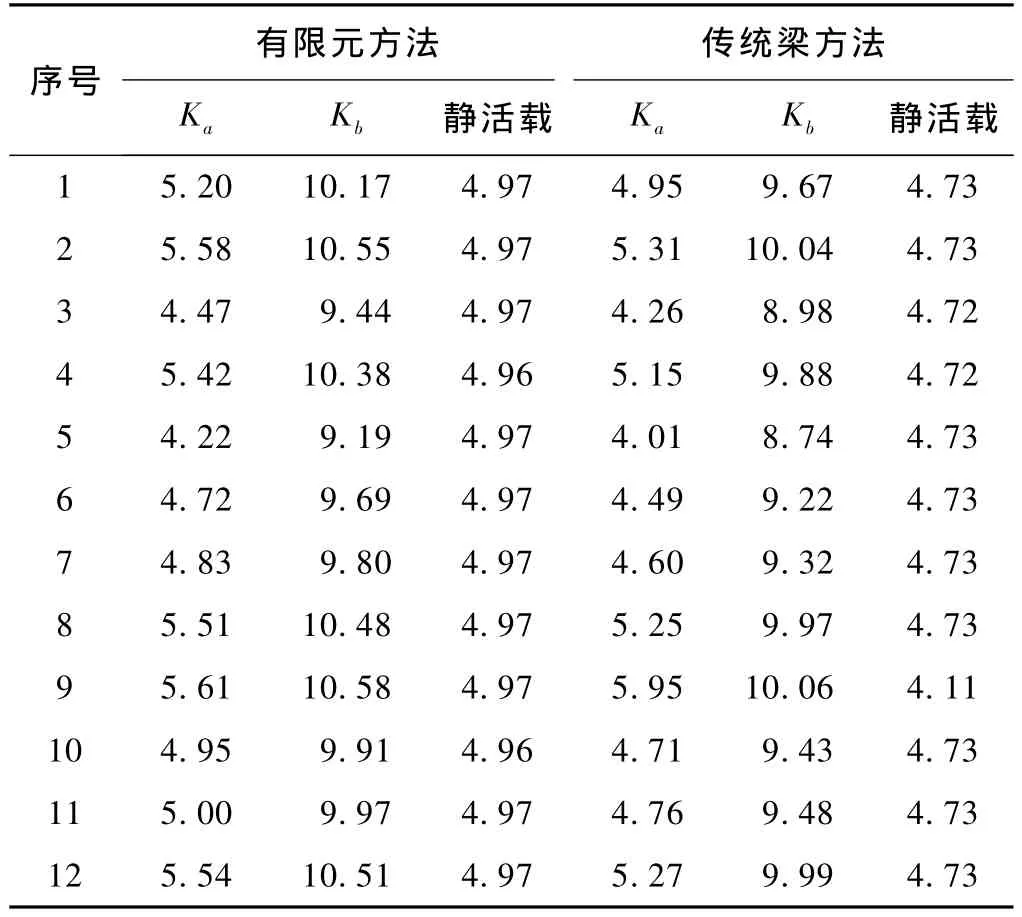
表3 跨中撓度計算值 mm

3 結論

通過對靜載試驗結果的分析，可得以下結論:

1)梁體跨中撓度實測值與計算值接近，與設計值相比有一定安全儲備，說明梁體剛度可靠，靜載試驗方案合理。

2)對于同一片梁，第一與第二加載循環在同一級荷載下，撓度值近似相等，說明梁體在試驗荷載下發生的變形是彈性變形。

3)不同梁在同一級荷載下撓度數值變化幅度稍大是由于梁體在彈性模量、二期恒載和試驗誤差等多方面不同引起的。

4)試驗梁第二循環加載至1.20倍設計荷載時，梁體撓度值與荷載保持線性關系，梁體下翼緣底部邊角及梁底面均未發現受力裂縫，說明梁體依舊處在彈性變形階段，梁體抗裂性滿足規范及設計要求。

［1］宋一凡.公路橋梁荷載試驗與結構評定［M］.北京:人民交通出版社，2002.

［2］荊龍江，王志堅，馬林，等.鐵路32 m預應力混凝土簡支梁靜載彎曲抗裂試驗［J］.鐵道建筑，2010(5):1-3.

［3］王彬.城市立交橋匝道曲線梁靜動載試驗［J］.長安大學學報(自然科學版)，2004，24(5):48-50.

［4］中華人民共和國鐵道部.鐵科技［2004］120號 客運專線預應力混凝土預制梁暫行技術條件［S］.北京:中國鐵道出版社，2004.

［5］中華人民共和國鐵道部.TB/T 2092—2003 預應力混凝土鐵路橋簡支梁靜載彎曲試驗方法及評定標準［S］.北京:中國鐵道出版杜，2003.

［6］孫訓方.材料力學［M］.北京:高等教育出版社，2002.