基于垂向振動的車體加速度分析

張 馨，李 會

(1.唐山軌道客車有限責任公司，河北唐山 063035;2.大連交通大學，遼寧大連 116028)

隨著鐵路貨運向重載方向發展，我國大秦線路開行了2萬t重載列車。C80B型敞車為大秦線專用運煤敞車，運營過程中車體鋼結構過早地出現破損問題，車體關鍵部位的疲勞開裂現象明顯增加，如:車體枕梁內側、上心盤頂面與中梁內側頂面、側柱與側板相交處等關鍵部位出現裂紋，其主要原因為車輛運行過程中的振動造成的疲勞破壞。車輛振動時的大部分能量集中在低頻振動，也就是車體浮沉、滾擺、點頭、搖頭等基本形式的典型振動組合的復雜振動。這就有必要考慮車輛運行過程中的典型振動對車體動態性能的影響。

從目前研究情況看，對車輛垂向力的研究大多單純停留在靜態分析水平，很少考慮車輛的典型振動對車體動響應的影響問題。車輛在實際運行中主要受軌道不平順的激勵，是產生車輛各種振動的主要根源。軌道垂向不平順會引起車輛的點頭振動和滾擺振動，同時又會引起輪重波動，不但增大輪軌垂向力和車體垂向加速度，而且影響線路的穩定性，降低運行的平穩性與安全性。車輛的運行平穩性就是指車輛在鋼軌上運行時的平穩程度。車輛的運行平穩性通常用“平穩性指標”或“振動加速度”來評定。因此，從垂向激勵引起的典型振動入手，采用結構動力學理論和有限元分析技術，建立C80B型敞車整車有限元模型，以軌道垂向不平順作為動力學邊界條件，模擬計算車輛在不同軌道激勵頻率下發生的典型振動，并進行動響應計算，獲得車體關鍵部位的動響應時間歷程，分析車體關鍵部位的加速度。然后根據波長和頻率的對應關系，通過改變激勵波長設計不同頻率的軌道不平順，進一步探討軌道激勵頻率對車輛運行穩定性的影響。

1 建立模型

1.1 建立整車有限元模型

由于分析的是整車的振動特性，需要設計適當的軌道載荷激勵作用于輪對使車輛發生典型振動，因此需要建立包括車體和轉向架在內的整體結構模型。建立C80B型敞車模型包括轉向架及車體底架、側墻、端墻等結構。轉向架采用四面體實體單元來模擬，車體底架、側墻、端墻等結構均使用四邊形薄殼單元來模擬，劃分有限元網格為37 626個，節點為25 323個。整車有限元模型見圖1。

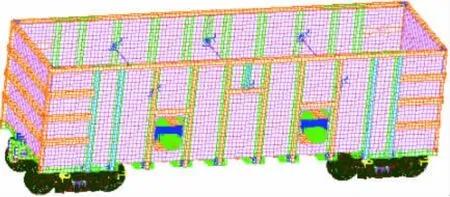
圖1 C80B型敞車整車有限元模型

1.2 載荷模型

車輛振動時的大部分能量集中在低頻振動，這種振動是由基本的典型振動組合而成的復雜振動。在進行模態分析的基礎上，確定了軌道激勵頻率的范圍，激勵頻率選擇在0.5～4 Hz的12個頻率。軌道不平順的函數形式用具有代表性的正弦函數作為激勵［1］。通過改變激勵頻率，用12個不同頻率的正弦激勵作為軌道激勵作用于輪對，進行動響應分析得到哪些頻率對車體的動應力有影響。軌道不平順的波形、波長、幅值、速度及線路狀態是設計軌道激勵的關鍵因素。軌道波形見圖2。

圖2 軌道波形

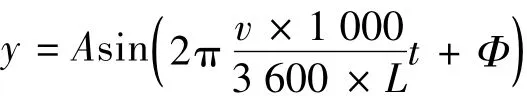
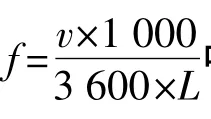
式中:y為波形;A為軌道不平順的幅值;v為通過速度，取120 km/h;Φ為軌道不平順的相位，兩股鋼軌取同相位;t為時間，設為60 s;L為軌道不平順的波長。

幅值、速度及線路狀態的確定:假設軌道狀態為長度2 000 m的直線軌道，貨車車輛(C80B)以速度v=120 km/h在單一諧波不平順激擾作用下行駛，根據我國《鐵路線路維修規則》［2］，軌道不平順值的最小極限值IRmin=4 mm，最大極限值為IRmax=9 mm。根據京滬線下行軌檢車采樣數據測得，經過約5萬t運量，實測軌道平均下沉4.41 mm［3］。所以本文假設軌道高低隨機不平順幅值A在0～5 mm范圍內變化。

軌道上存在著各種波長的不平順，從數十毫米到數米甚至數十米，甚至超過百米的波長都存在，本文參考貨車不平順的不利波長為10～20 m［4］。由頻率公

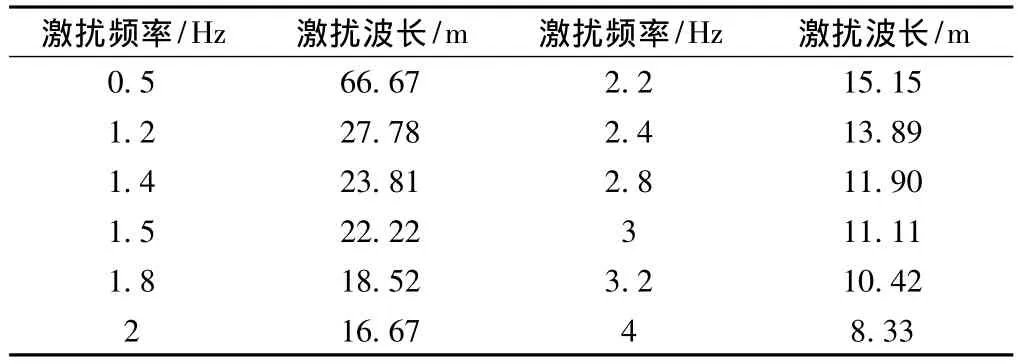
表1 軌道激擾頻率波長關系

綜上所述，根據表中頻率和波長的關系設計波形，會得到12組不同頻率的軌道激勵模式，按照模擬車輛點頭和滾擺振動的線路形式分別作用于對應的輪對，進行動響應計算，即可獲得車體關鍵部位的動響應，進行動響應分析。

2 振動過程動響應分析

模擬車輛在設計的典型線路上運行，考察設計線路上車體的主要振動形式，討論振動過程中車體的彈性表現，分析車輛振動過程不同振動形式對車輛穩定性的影響，探討軌道激勵波長對運行穩定性的影響。

2.1 確定振動形式

模擬的軌道激勵的目的是使車體發生垂向典型振動，為了驗證振動形式，查看振動過程位移時間歷程對應的位移云圖，圖3為不同頻率的軌道不平順線路行駛，模擬的2種軌道形式下的車體位移云圖。

圖3 振動過程位移云圖

從位移云圖3可知，模擬的軌道激勵使車體發生了滾擺和點頭振動，說明設計的激勵模型是可行的。

2.2 車體加速度分析

加速度是評定車輛運行穩定性的重要指標，下面對2種振動過程的加速度進行分析，探討不同的垂向振動對車輛運行穩定性的影響。圖4為點頭振動過程中車體枕梁處節點加速度時間歷程。

由圖4可以看出，車體枕梁加速度曲線成周期變化，隨著激勵頻率的升高，周期數量增多，加速度幅值增大。頻率為1.5 Hz時，加速度最大值為1.7 m·s-2;頻率為2.4 Hz時，加速度最大值為6 m·s-2;根據貨車運行品質標準及評定，車體垂向加速度小于2 m·s-2時為優等;在2.0～3.5 m·s-2為良好;在3.6～4.5 m·s-2為滿意;在4.6～6.5 m·s-2為容許;6.5 m·s-2時不能長期運用，屬于強度不利的條件;大于7.0 m·s-2時長期運用存在危險，有損車輛強度。上述2個激勵頻率產生的加速度均在可以接受的范圍，沒有達到破壞的程度，對車體來講是安全的。但是激勵頻率在2.4 Hz時，加速度6 m·s-2有些高，應該引起注意，說明此頻率的激勵對車體的影響很大。下面進一步探討2種振動過程車體枕梁、底架中心點、底架角點加速度與激勵頻率的關系，圖5為車體枕梁節點加速度絕對值與激勵頻率在2種振動下的數值關系圖。

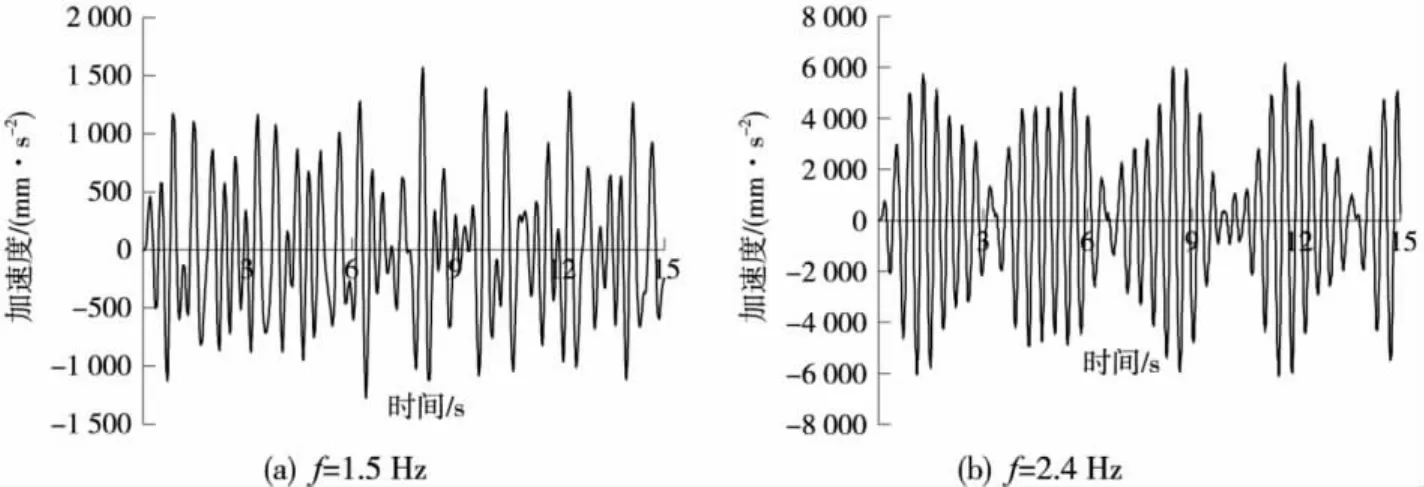
圖4 點頭振動枕梁節點加速度

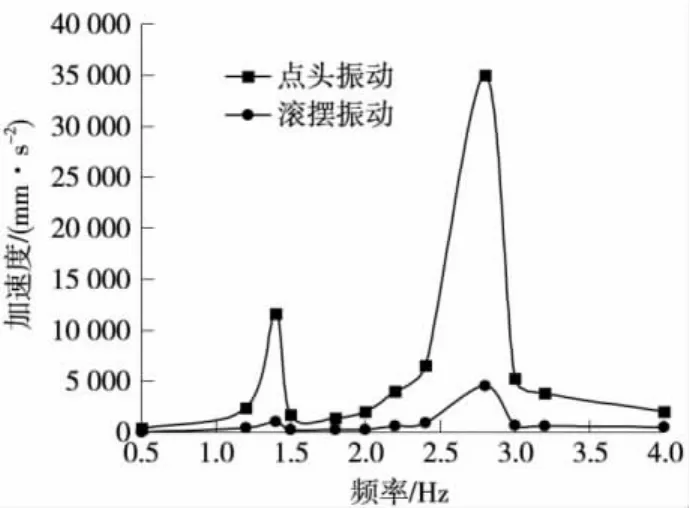
圖5 枕梁節點加速度-頻率關系

由圖5可知，2種振動過程，車體枕梁加速度隨著激勵頻率的升高幅值增大，加速度曲線隨頻率的變化趨勢相近，均在1.4、2.8 Hz時出現峰值，加速度最大值出現在2.8 Hz。點頭振動的最大加速度為36 m·s-2，已經大大超出安全范圍，車體在此條件下屬于危險運行，對車體強度破壞很大。滾擺振動最大加速度為4.8 m·s-2，沒有超出安全范圍，貨車運行品質評定為容許。激勵頻率在1.2～1.5 Hz、2～3.0 Hz時加速度上升明顯，這幾個頻率對車體強度影響非常大，車體枕梁加速度對這幾個激勵的頻率比較敏感。圖6、圖7為車體底架中心節點和底架角點加速度-頻率關系。

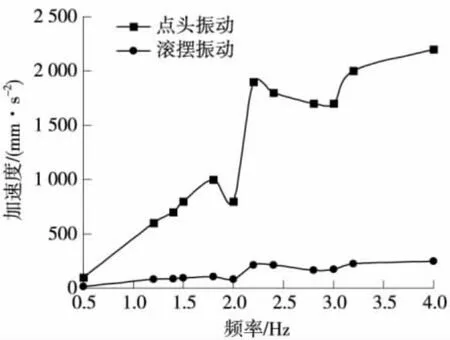
圖6 底架中心節點加速度-頻率關系

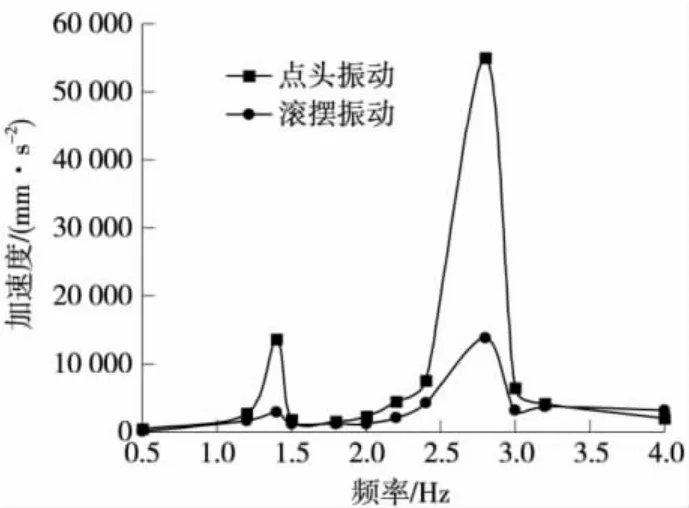
圖7 底架角點加速度-頻率關系

由圖6、圖7可知，車體不同部位的加速度與激勵頻率變化關系基本接近，各部位加速度幅值不同，點頭振動加速度幅值在考察頻率范圍內均大于滾擺振動加速度的幅值，2種振動加速度幅值隨激勵頻率的變化趨勢基本一致。2種振動情況下，車體關鍵部位加速度幅值隨著激勵頻率的升高增大。點頭振動車體中心加速度最大值出現在4 Hz，最大加速度為2.4 m·s-2，沒有超出安全范圍，貨車運行品質評定為良好。車體底架角點加速度最大值出現在2.8 Hz，最大加速度為58 m·s-2，已經大大超出安全范圍，車體在此條件下屬于危險運行，對車體強度破壞很大。滾擺振動中心點加速度最大值出現在4 Hz，最大加速度為0.24 m·s-2，沒有超出安全范圍，貨車運行品質評定為優等。車體底架角點加速度最大值出現在2.8 Hz，最大加速度為15 m·s-2，超出安全范圍。上述情況是模擬軌道理想化的情景，在實際中不可能出現，但是在1.2～1.5 Hz、2～3.0 Hz的激勵是特別需要注意的，即在速度為120 km/h時，11.11～16.67 m、22.22～27.78 m的軌道波長是需要注意避免的。

3 結論

從模擬車輛發生垂向振動入手，對振動過程車體的加速度進行分析。通過改變軌道激勵頻率的方式，探討車體關鍵部位加速度與激勵頻率的關系，得出以下結論。

(1)設計的軌道載荷達到預想結果，車體點頭和滾擺振動發生。

(2)2種振動對車體加速度的影響不同。點頭振動對加速度的影響比滾擺振動劇烈得多。結合實際車體破損情況，車輛在線路運行過程可能發生點頭振動比較多。

(3)車輛發生垂向振動時，車體加速度隨激勵頻率升高幅值增大，周期數增多。頻率在2.0～3 Hz時對車體加速度影響很大，激勵頻率在2.8 Hz時對車體的影響最大，加速度達到最大值，是與車輛自振頻率耦合的結果，在設計中要考慮避免這種頻率的激勵。

［1］翟婉明.車輛-軌道耦合動力學［M］.北京:科學出版社，2007:12-73.

［2］練松良，黃俊飛.客貨共運線路軌道不平順不利波長的分析研究［J］.鐵道學報，2004，26(2):111-115.

［3］嚴雋耄.車輛工程［M］.北京:中國鐵道出版社，2003:405-451.

［4］魯寨軍，田紅旗，周 丹.270 km/h高速動車模態分析［J］.中國鐵道科學，2005，26(6):18-23.

［5］王福天.車輛系統動力學［M］.北京:中國鐵道出版社，1994:89-102.