基于窮盡熵優化的混沌圖像加密

寧 磊， 王振永， 楊明川

(哈爾濱工業大學 通信技術研究所，哈爾濱 黑龍江 150001)

0 引言

隨著世界范圍的數字圖像傳輸的迅速發展，安全問題成為了人們關注的重要問題。許多諸如電纜電視，軍用圖像數據庫，生物測量鑒定系統以及在線個人照片相冊要求具有魯棒安全性的系統來存儲和傳輸數字圖像。

傳統的密碼學算法諸如DES、IDEA和RSA算法不能很好的適用于快速通信應用。而混沌的顯著特點是對初始值的敏感依賴性，這使得混沌系統成為密碼學方案的一個有前景的另一種選擇。基于混沌的加密處理在 1989年[1]被首次提出，從那時開始，許多基于混沌系統的其他方案相繼被提出。

許多密碼學系統的安全性都是基于隨機數發生器。產生隨機序列的發生器能夠歸納為2大類：真實隨機數發生器和偽隨機數發生器。真實隨機數發生器具有非確定信源的優勢，比如隨著放射性延遲時間殆盡的熱射噪聲源，混沌電路以及半導體容量管理數量等。偽隨機數發生器通過系統模型產生隨機數，產生的隨機數隨機性較弱，容易攻克。近年來，數字電路的廣泛發展使得后者實現的成本變得低廉。這就需要找到一種增強偽隨機數發生器偽隨機性能的方法。

圖像加密的思想可歸結為3大類：象素置亂法[2]、位置置亂法[3]和前2類方法的結合[4]。其中象素置亂就是將某個序列與象素值進行某種相關運算，如異或運算。解密過程也很簡單，只要用原始序列與加密圖像的象素值進行相關逆運算即可。

我們知道作為加密序列，不僅窮盡步長要大，而且窮盡過程的每個組成部分中的序列長度要盡量相等。為此，提出用窮盡熵來衡量序列的類隨機性強弱，選擇經過熵選擇即優化后的混沌序列采用象素置亂法對圖像進行加密。最后，安全分析表明此加密方案具有對抗已知統計性攻擊的魯棒性。

1 序列的窮盡熵

序列窮盡熵的概念是建立在序列的生成和再生的基礎上提出的。序列的生成和再生是不同的。再生是序列自我的簡單復制過程，而序列的生成中復制序列的最后一個序列值是可以變化的。具有強偽隨機性的序列，不僅窮盡步長要大，而且窮盡過程的每個組成部分中的序列長度要盡量相等。文獻[5]提出了一種利用窮盡熵衡量序列隨機性強弱的方法。將序列的各個窮盡部分(包括最后一個不是窮盡的組成部分)在整個序列中占的比率近似地看作其出現的概率 ，然后用式(1)：

來計算整個序列的類隨機性強弱。由序列窮盡的概念和最大熵定理可知，序列窮盡步長越長，各窮盡組成部分的概率越是近似相等，則整個序列的窮盡熵越大，序列的類隨機性也就越強。

例如：

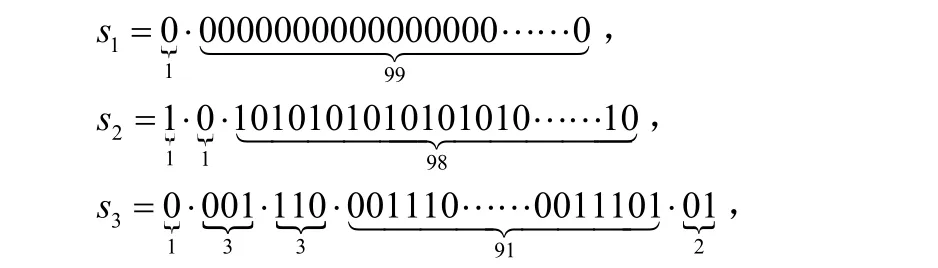
根據表達式（1），序列S1,S2,S3的窮盡熵分別為 0.0243哈特、0.0486哈特和0.1826哈特。窮盡熵越大，序列攜帶的信息越多，進而序列的隨機性就越強。

2 混沌序列的產生

混沌系統模型有很多種，我們選擇比較典型的 Lorenz混沌系統作為混沌序列發生器，它的數學表達式如下：

在表達式（2）中，a、b和c是系統參數，當a=10、b=8 3和c=28時, 保證 Lyapunov 指數λn＞0。系統處于混沌狀態。

Lorenz系統可以產生三維混沌實序列，我們只取其中一維。由于其產生的是隨機實數，作為加密序列，還需要對混沌序列進行二值量化。文獻[6]提出了很多種量化方法，為了方便，將利用表達式（3）將實數序列映射到[- 0.5,0.5]之間，然后通過表達式（4）獲取二值序列。

在上述表達式中，bn是由Lorenz系統產生的混沌序列，int(bn)是對序列bn取整運算，Bn是量化后的二值序列。

3 熵優化的混沌序列及圖像加密

3.1 序列性能測試

候選的加密序列必須具有較強的偽隨機性。首先通過Lorenz系統產生原始的混沌序列，二值量化后，分成N組，通過計算窮盡熵，選擇熵最大的一組作為測試序列。該序列的自相關和互相關特性如圖1所示。

我們可以看出，其自相關函數接近δ函數，互相關函數接近零函數，這種良好的相關性，是對圖像進行加密的前提。

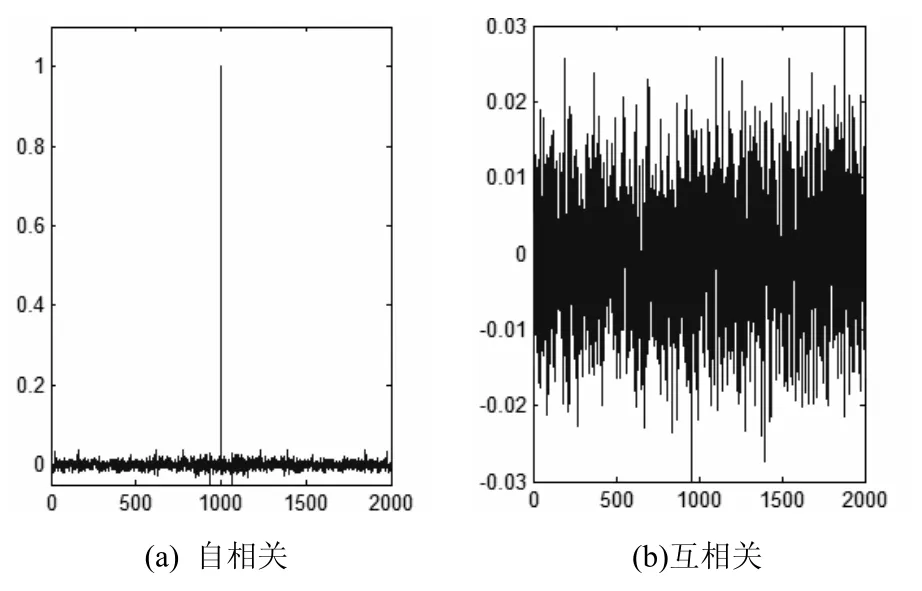
圖1 混沌序列的相關性分析

3.2 加密和解密方案

所提出的基于異或函數的圖像加密和解密方案在MATLAB中予以實現。該方案包括以下步驟：

①該方案首先找到明文圖像的大小為M×N，此處M表示圖像的行數，N表示圖像的列數，這些像素點被按照從左到右從上到下的順序排列，由此得到一個該圖像的數據集，其中的每項都是像素點的一個十進制灰度值（從0到255），然后將每個十進制數值轉換成等價的二進制數，最終得到一個一維矩陣B。

②矩陣A_candidate(n)是基于Lorenz混沌系統產生的二值序列，n代表候選序列的組數，利用窮盡熵的定義選擇熵最大的一組作為優選混沌序列A。

③將A和圖像矩陣B經過異或運算得到了第三個矩陣C，即C=A⊕B。

④這樣得到的矩陣 C通過第一步的相反過程轉換為一個加密編碼后的圖像，作為密文進行傳輸；

對于圖像的解密我們再次采用異或函數進行運算，即C⊕B=A。在圖2中我們可以看到大小為131× 131的Lena明文圖像，以及采用以上方案得到的加密后的密文圖像和解密后的明文圖像。

圖2 圖像加密恢復過程

4 安全性分析

一個好的加密方案應該具有魯棒性抵抗所有的密碼分析，統計性和窮舉攻擊。文章完成了所提出的圖像加密方案的一些安全性分析—柱形統計圖分析和2個相鄰像素的相關分析。

4.1 柱形統計圖分析

香農提出擴散和混淆的兩種方法用來防止統計性攻擊[7]。明文Lena圖像和所提出方案獲得的加密圖像的柱形統計圖如圖 3所示。比較柱形統計圖我們可以看出加密圖像的灰度值呈現均勻分布，其和明文圖像的柱形統計圖具有明顯不同。所以，加密后的圖像對于任何的統計性攻擊都具有安全性。

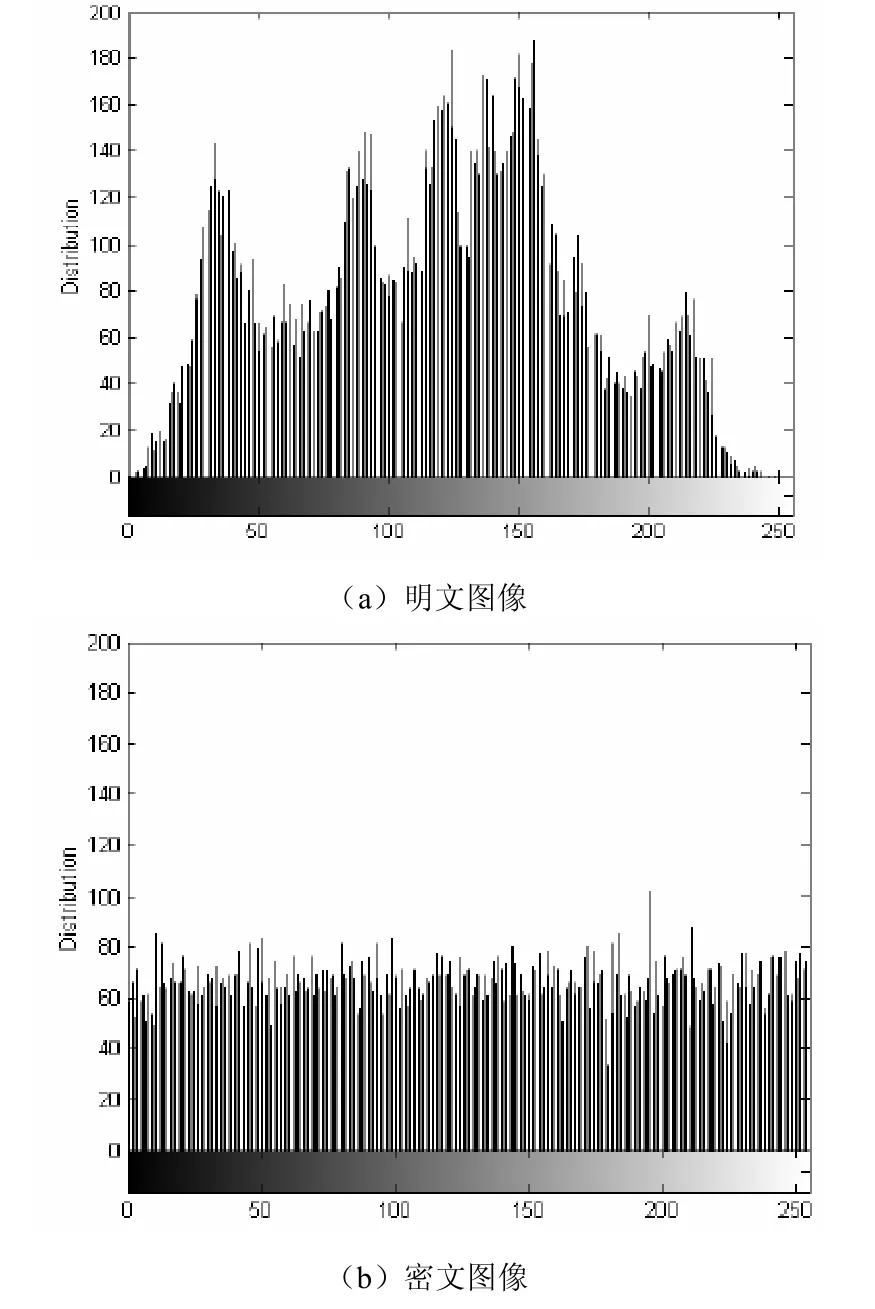
圖3 圖像柱狀統計

4.2 2個相鄰像素的相關分析

對于任意一個圖像，每個像素點無論在水平方向，垂直方向或者對角方向都與其相鄰的像素點高度相關。為了測試在明文圖像中像素點的相關性，以及在加密圖像中像素點的相關性，我們利用以下公式計算了每個像素對的相關系數γ[8]。

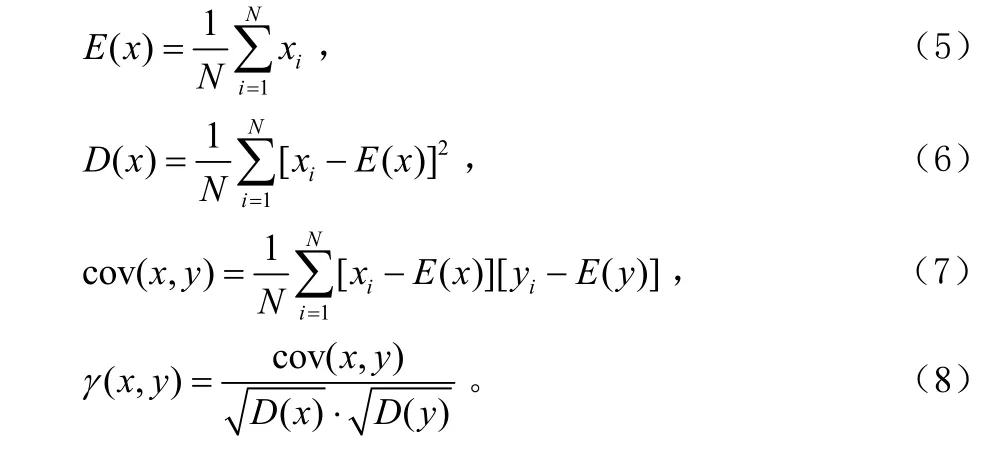
這里x和y是圖像中2個相鄰像素點的灰度值，N是像素點相鄰像素對的總個數。在明文圖像和密文圖像中的2個水平相鄰像素點的相關性如圖4所示。

在表1中我們發現密文圖像的在任意方向的相關系數都近似等于零，所以密文圖像具有很小的關聯性。

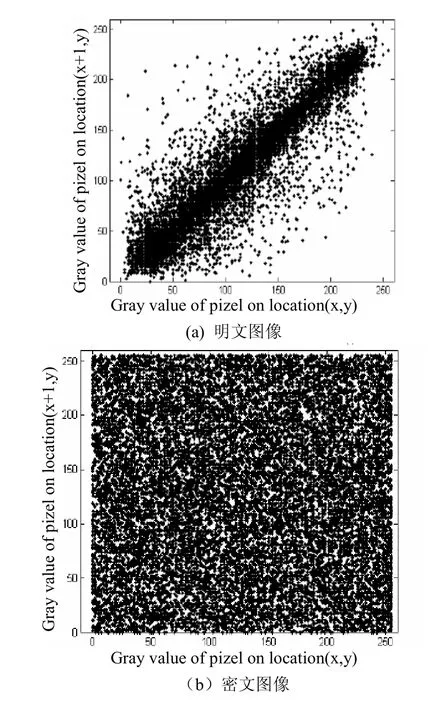
圖4 圖像中相鄰兩像素的相關

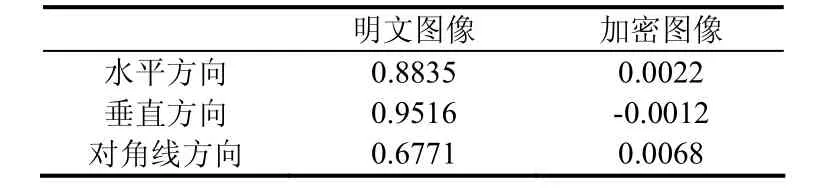
表1 兩種圖像中兩相鄰像素的相關系數

5 結語

文章提出了一種基于窮盡熵優化的混沌圖像加密方案。通過利用窮盡熵來度量序列的類隨機性強弱，選擇熵最大的一組混沌序列對圖像進行加密。最后，安全分析表明此加密方案具有對抗已知統計性攻擊的魯棒性。

[1]MATTHEWS R. One the Derivation of a Chaotic Encryption Algorithm[J]. Cryptologia, 1989(08):29-42.

[2]陳永紅，黃席樾. 一種混沌系統的設計及其在圖像保密變換中的應用[J].計算機應用, 2004,10（26）:52-55.

[3]唐林山，江成順. 一種結合混沌的熱流密碼圖像加密算法[J].計算機工程與應用,2007,43（03）:37-39.

[4]閔連權. 基于雙置亂的圖像加密算法[J].測繪科學, 2006,31（03）:71-73.

[5]FENG M. Analysis on Random-like Property of Chaotic Motions with Exhaustive Entropy[C]. Automation and Logistics, 2007 IEEE International Conference on, 2007: 2420-2425.

[6]KOHDA T, TSUNEDA A. Statistics of Chaotic Binary Sequences[J].IEEE Transactions on information theory,1997,43(11):104-112.

[7]SHANNON E. Communication Theory of Secrecy System[J]. J. Bell Syst. Tech., 1949(28):656-715.

[8]CHEN G R, MAO Y B, CHARLES K. A Symmetric Image Encryption Scheme based on 3D Chaotic Cat Maps[J]. Chaos, Solitons and Fractals, 2004(21):749-761.