非線性函數法研究曲率對彎箱梁橋的影響

宋國華，霍 達，羅 玲，3，王東煒

(1.鄭州大學 土木工程學院，湖南 鄭州 450001;2.北京工業大學 建筑工程學院，北京 100022;3.北京市市政工程設計研究總院，北京 100045)

彎橋和直橋相比，最大的不同點主要在于曲率所引起的彎扭作用的耦合。一般而言，這種彎扭聯合作用，隨著曲率和橋寬的減小而減小。

研究表明，圓心角、曲率半徑、弧長、橋面寬度以及彎扭剛度比等，是區分曲梁、直梁受力特征的主要因素［1］。除了影響直線橋受力特性的因素，如跨長、抗彎剛度外，與彎橋有關的主要因素還有圓心角。主梁的彎曲程度是影響彎橋受力特性最重要的因素，能全面反映主梁彎曲程度的參數是圓心角，它是跨長與半徑的比值，反映了與跨徑有關的相對彎曲關系。如果橋梁跨長一定，主梁圓心角的大小就代表了梁的曲率，圓心角越大，曲率半徑就越小，所顯示的彎橋的受力特點就越明顯［2］。

本文主要研究橋長L和圓心角φ對二等跨連續彎箱梁橋的結構反應的影響。提出以梁格系法為理論基礎編制的“斜彎坡及異形空間分析軟件系統3DBSA”為結構計算分析工具，以 Matlab為數據處理工具，用非線性函數法建立變截面兩跨彎箱梁橋受力性能與圓心角及橋長間的顯示函數關系。

1 模型建立

研究參數有圓心角 φ、橋長L，它們的取值范圍如下:

1)φ:30°，60°，90°，120°，150°。

2)L:50，70，80，100，130，150 m。

這樣共建立6×6=36個模型。

1.1 截面特性

選用單箱單室截面，上寬9．0 m，下寬5.0 m，兩翼板寬度各為2.0 m，頂板厚0.20 m，底板厚0.35 m，兩側上翼緣板根部厚0.30 m，端部厚0.15 m，直線過渡。橋梁跨中高度取為單跨長的1/40，支座高度取為單跨長的1/18，其它截面高按二次插值生成。各模型的支座截面高度和跨中截面高度的取值見表1。圖1、圖2分別列出了圓心角 φ=90°，橋長 L=130 m模型的支座截面和跨中截面。

圖1 支座截面(單位:mm)

1．2 收縮徐變

按文獻［3］規定，取混凝土加載齡期τ=10 d。各模型的收縮徐變參數的取值見表1。

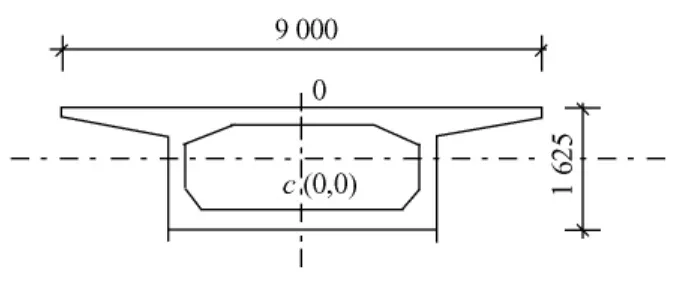
圖2 跨中截面(單位:mm)

表1 收縮徐變參數及截面高度

1.3 活載

取汽車—超 20級，掛車—120，人群荷載為 3.5 kN/m2，縱向加載步長 1.0 m，橫向加載步長 0.5 m。左右車道數均為1，單列系數1，行車時速80 km/h。

1.4 荷載組合

按規范規定取正常使用極限狀態和承載能力極限狀態下的荷載組合，共有8種。模型建立其它相關內容參見文獻［4］。圖3為圓心角 φ=90°，橋長 L=130 m的模型在施工階段4，即收縮徐變完成后的結構分析簡化模型。

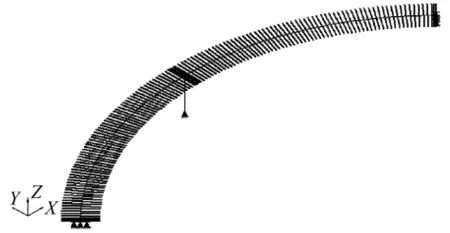
圖3 結構分析簡化模型

1.5 模型計算

包括4部分:數據處理，施工計算，活載計算及荷載組合。由軟件3D-BSA計算。

所關心的結構反應包括分別在正常使用極限狀態和承載能力極限狀態下控制截面的內力和局部坐標系下自重作用的位移，以及組合1和組合2工況下支承單元的反力。因為上述內力為截面的配筋內力，上述位移最能反映結構變形受參數的影響情況，而支承反力反映了支承本身受φ，L兩個參數影響的變化情況。

2 非線性函數法數據處理

Matlab中的函數lsqnonlin()是一個可以方便地擬合出多變量公式的函數，它解決的是非線性最小二乘問題，包括非線性數據擬合問題。lsqnonlin()要求用作者定義的函數來求解向量定義的函數。x=lsqnonlin(fun，x0)以輸入初始點 x0開始，求出 fun中所列函數的平方和的最小值。fun返回的是這些值所組成的向量{x}。本文擬合的數值是各種橋梁結構反應，包括內力、位移和支座反力。

該方法的優點是:可以擬合多變量公式，并能整體考慮所有變量的影響。缺點是:需要提前預設所需擬合公式的形式并輸入各變量的初始點。另外，如果變量較多，擬合效果不夠理想時，需多次調整初始變量值，以達到能滿足要求的較優點(極值點)，這是一個優化的過程。本文所確定的擬合標準，是擬合值與原值相差不超過10%。

本文擬合出的結構反應與橋長及圓心角之間的函數關系為:x1φx2Lx3+x4，見表 2。通過分析 x1，x2，x3和x4之間的符號變化就可以確定結構反應與橋長及圓心角的增減關系。分析后可以發現:

1)當x2=0或x2≈0時，不受圓心角影響，或影響很小，可忽略不計。

2)當x3=0時，不受橋長影響。

3)當x1x2＞0時，隨圓心角的增大而增大。如x3＞0，則增大程度隨橋長的增大而增大;如x3＜0，則增大程度隨橋長的增大而減小。

4)當x1x2＜0時，隨圓心角的增大而減小。如x3＞0，則減小程度隨橋長的增大而增大;如x3＜0，則減小程度隨橋長的增大而減小。

5)當x1x3＞0時，隨橋長的增大而增大;如 x2＞0，則增大程度隨圓心角的增大而增大;如x2＜0，則增大程度隨圓心角的增大而減小。

6)當x1x3＜0時，隨橋長的增大而減小。如 x2＞0，則減小程度隨圓心角的增大而增大;如 x2＜0，則減小程度隨圓心角的增大而減小。

將符合以上條件的反應項目列于表3。

下面分析所擬合結果的可靠性，通過對Qymax(承)的擬合值與原值之差相對于原值的比值作一例子，比值結果見表4。

由表4可知，比值結果均在10%以內，說明用非線性函數法擬合彎箱梁橋結構反應與圓心角及橋長的關系還是可行的，結果也比較可靠。

通過以上分析可得如下結論:

1)所有結構反應均受到橋長的影響，不可忽略。

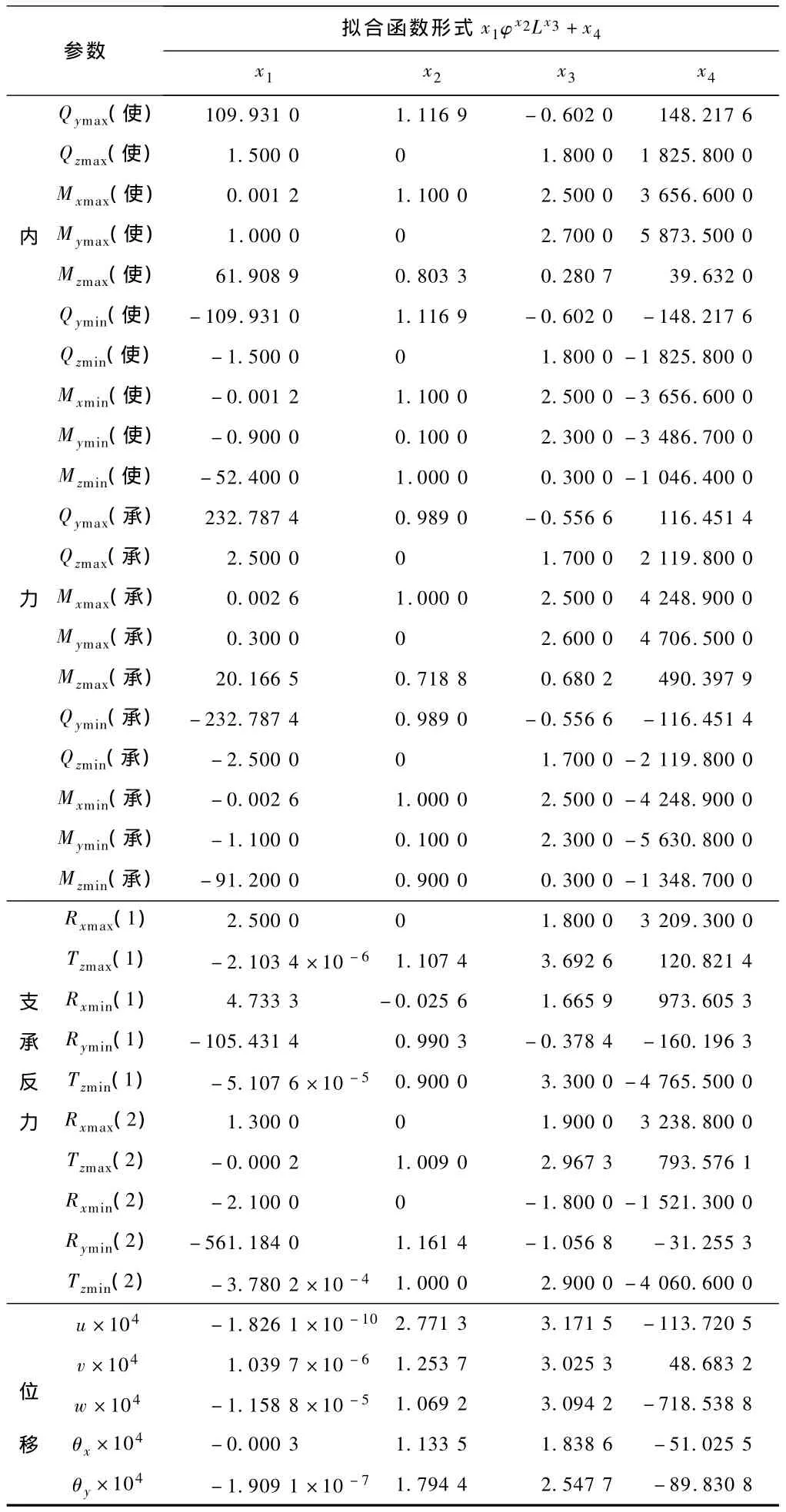
表2 結構反應與橋長及圓心角的擬合函數關系力:kN;位移:m

2)在直梁橋設計計算中存在的主要內力，如Qz，My以及支承反力Rx受圓心角φ影響很小，在彎橋設計中可以不考慮圓心角的影響，而取橋梁中心線長度為跨長來計算彎橋中的內力Qz，My及反力Rx。

3)因曲率存在而使彎橋中產生的附加內力，如Qy，Mx，Mz，支承反力 Ry，Tz及各項位移受圓心角 φ 影響較大，設計時必須考慮圓心角的影響。

表3 各種結構反應受圓心角及橋長影響的分類

表4 Qymax(承)的擬合值與原值之差相對于原值的比值

4)內力 Nx、位移 θz及支承反力 Rymax絕對值均很小，可忽略不計。

3 結論

1)通過統計分析和數值模擬的方法擬合出橋梁結構反應與圓心角及橋長間的顯示函數關系，方法可行，結果可靠。

2)用非線性函數法擬合的橋梁結構反應，可以用其變量間的符號關系表達出結構反應受變量影響的增減性。

［1］邵榮光，夏淦．混凝土彎梁橋［M］．北京:人民交通出版社，1994．

［2］CHAN T H T，YUNG T H．A theoretical study of force identification using prestressed concrete bridges［J］．Engineering Structures，2000(23):1529-1537．

［3］中華人民共和國交通部．JTG D62—2004 公路鋼筋混凝土及預應力混凝土橋涵設計規范［S］．北京:人民交通出版社，2004．

［4］宋國華，羅玲，王東煒．偏心支承對120°圓心角雙跨彎箱梁橋的影響［J］．橋梁建設，2005(4):44-47．