基于Pareto最優解的零件制作方向優化研究

劉厚才， 廖艷春

?

基于Pareto最優解的零件制作方向優化研究

劉厚才， 廖艷春

（湖南科技大學機電工程學院，湖南湘潭 411201）

分析了快速成型工藝中零件制作方向對制件表面質量、所需支撐面積和零件制造時間的影響，分別建立了它們的優化數學模型。采用了基于Pareto最優解的多目標優化遺傳算法NSGA－II進行優化計算，通過與單目標優化方法求得最優結果的對比，表明用多目標優化方法進行零件制作方向的優化計算，不僅可以求出比單目標方法更優的解，而且通過一次優化計算就可得到多個較優的零件制作方向。

計算機應用；快速成型；多目標優化；零件制作方向；Pareto最優解

在快速成型技術的制造過程中，零件的制作方向是一個非常重要的工藝參數，它直接影響制件的表面質量、支撐結構、制作時間等指標，并最終影響著零件的制作成本。在當前許多商品化的快速成型系統中，零件的制作方向仍然靠用戶人工選擇，這樣，零件制作方向的選擇在很大程度上取決于用戶的經驗和主觀技巧。對于形狀和結構較簡單的零件一般憑直覺或經驗比較容易確定一個較好的零件制作方向，但是對于形狀和結構較復雜的零件就很難憑直覺或經驗選出一個較優的零件制作方向，而且大多數用戶不具備這種能力。為了解決這個問題，國內外研究人員通過采用不同的方法對零件制作方向與這些指標的關系進行過理論分析與研究，建立零件制作方向的優化數學模型，并對優化模型進行數值求解，以實現對任意形狀和結構零件制作方向的自動優化方法。零件制作方向的優化是一個多目標優化問題，目前有關零件制作方向的優化研究要么進行的只是單目標優化研究，要么就是先通過線性加權法將多目標優化問題轉化為單目標優化問題，再采用單目標優化方法求最優解。這是一種先決策后搜索的尋優模式，本質上仍然屬于單目標優化，其存在如下明顯的不足：第一，目標權重作為決策者的一種偏好信息，一般很難預先確定；第二，每次計算只能產生一個最優解，且優化結果對權重系數的分布很敏感；第三，決策者往往希望提供多種方案以供選擇，而該方法只能提供唯一解。為此，本文將基于Pareto最優原理的多目標優化方法用于快速成型工藝中零件制作方向的優化研究，為零件制作方向的優化研究提供了一種新思路，該方法經過一次優化計算就可以獲得各目標在不同權重分配情況下零件制作方向的多個最優解的集合（即Pareto最優解集）。該方法更好地反映零件制作方向多目標優化的實質，可以實現了真正意義上的零件制作方向的多目標優化。

1 多目標的優化模型

根據已有的研究成果可知，在快速成型加工過程中受零件制作方向影響最大的主要是3個指標：零件的表面質量、零件所需的支撐和零件的制作時間。本文也選用這3個指標作為對快速成型工藝中零件制作方向進行優化的目標。

1.1 以表面質量為目標的優化模型

在快速成形技術中，零件的制造過程是先對三維模型進行二維離散，然后再用二維離散數據堆積成三維實物，因此，在零件的傾斜表面上會留下大量的呈樓梯狀臺階，這在快速成形技術中被稱為臺階效應(staircase effect)，是由快速成形的固有成形原理帶來的。臺階效應會導致實際的零件表面與期望的零件表面存在一定的體積誤差。易知通過減少因臺階效應產生的體積誤差，可以提高零件的表面質量，因此以零件表面質量為優化目標可以通過選擇一個零件制作方向，使因臺階效應產生的體積誤差最小來實現。

在快速成形工藝中，零件模型的接口文件一般都是采用STL文件格式，STL文件是通過用三角形面片的方法來逼近模型表面。假設用表示第個三角形面片的外法線方向的單位矢量，A表示該面片的面積，表示與之間的夾角，面片的3個頂點坐標為：P(x,y,z), P(x,y,z)，P(x,y,z)。是選定的在模型坐標系下零件制作方向的單位矢量，是零件制作方向與軸之間的夾角，是零件制作方向在平面上的投影與軸之間的夾角，則有。

以零件表面質量為目標的優化模型可表述如下

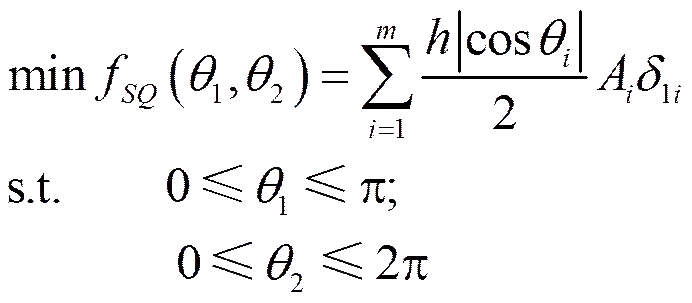
式中為零件模型的三角面片的個數

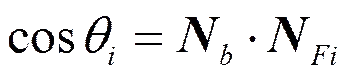
1.2 以支撐為目標的優化模型

快速成型工藝中，在零件的懸空部位下面一般需要設置支撐。本文在進行制作方向優化時只考慮支撐面積，且只計算外法線朝下的三角形面片的面積。因此，以減少支撐為優化目標的模型如下

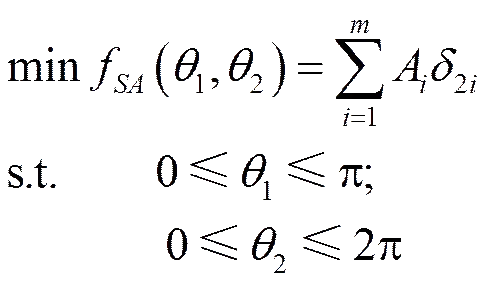
1.3 以制作時間為目標的優化模型

在快速成型工藝中，通過降低零件在z軸方向上的高度可以大大減少零件的切片層數，進而可以較多地減少制作時間。因此，減少零件的制作時間可以通過使零件在制作方向上的高度最小來實現。

設P(x,y,z)是零件模型中某一三角形面片的一個頂點的坐標，該頂點用向量表示為[x,y,z]，=1，2，…，，是零件模型中頂點的個數。則以制作時間為優化目標的模型可表示如下

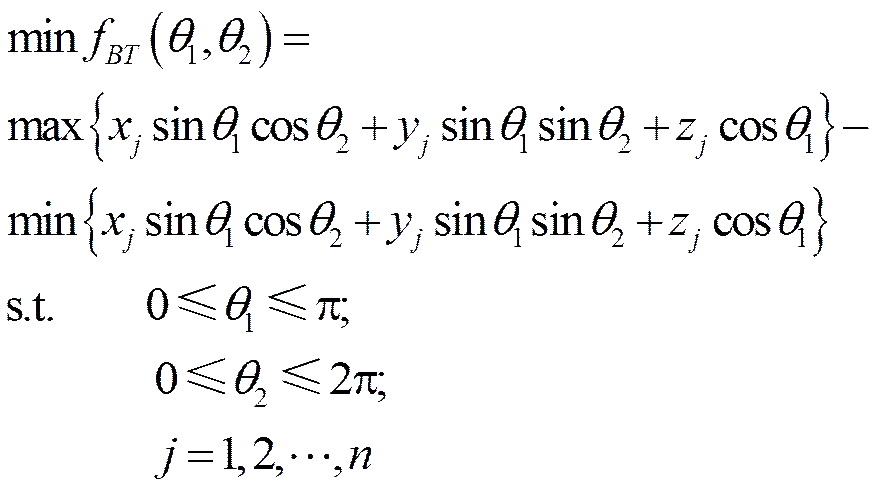
2 優化模型的求解

2.1 求解方法

關于優化問題的求解主要有兩類方法：解析法和直接法。解析法只適用于優化的目標函數及約束有明確的解折表達式的情況。直接法則是用直接搜索的方法，經過若干次迭代計算來搜索目標函數的最優解，直接法主要適用于目標函數較復雜或目標函數不能通過變量明確表示的情況。由優化目標模型式(1)、式(2)和式(3)可以看出，對這三個優化模型的求解只能采用直接法。

基于模擬生物進化過程的遺傳算法，是一種自組織全局優化的概率搜索算法，具有群體學習功能、自適應進化等特點，而且能夠在單一種群中并行地處理一組解的集合，是求解多目標優化問題的有效方法。將Pareto最優原理與遺傳算法相結合形成的求解多目標優化問題的方法稱為多目標遺傳算法。多目標遺傳算法是在基本遺傳算法的基礎上發展來的，為了適應多目標優化問題求Pareto最優解的需要，算法中除了有基本遺傳算法中的選擇、交叉和變異算子外，還增加了種群分級排序、小生境處理和精英保留3個算子。迄今為止，研究人員已經提出了多種多目標遺傳算法，其中比較突出有第二代非支配排序遺傳算法(NSGA-II)，該算法具有穩定的收斂性和較好的全局最優解搜尋能力，已成為了目前求解多目標優化問題的標準算法之一。本文就采用NSGA-II算法來進行零件制作方向的多目標優化求解。

2.2 求解算法的流程

基因編碼方法采用二進制編碼方式，取求解精度0.1o，初始種群的產生采用隨機產生方式。種群分級排序、小生境處理、選擇、雜交、變異和精英保留算子采用NSGA-II算法。算法的終止條件設定為進化的代數達到設定的最大的代數，求解算法的流程如圖1所示。

圖1 求解算法流程

3 優化實例分析

根據上述的算法原理，在Windows XP操作平臺上用Visual C++ 6.0編寫了快速成型工藝中零件制作方向的自動優化計算程序。為了檢驗優化的效果，本文選用了如圖2所示的2個模型樣件進行測試，圖2(a)是一導軌滑塊模型，由60個三角形面片組成，圖2(b)是一個螺旋槳模型，由16992個三角形面片組成。圖2(a)取自文獻[2]，是零件制作方向優化研究中常用的模型，文獻[14-17]通過單目標優化方法求得它的最優制作方向如圖3所示，其中方向1是以表面質量為目標的最優制作方向，方向2是以減少支撐為目標的最優制作方向，方向3是以制作時間為目標的最優制作方向。

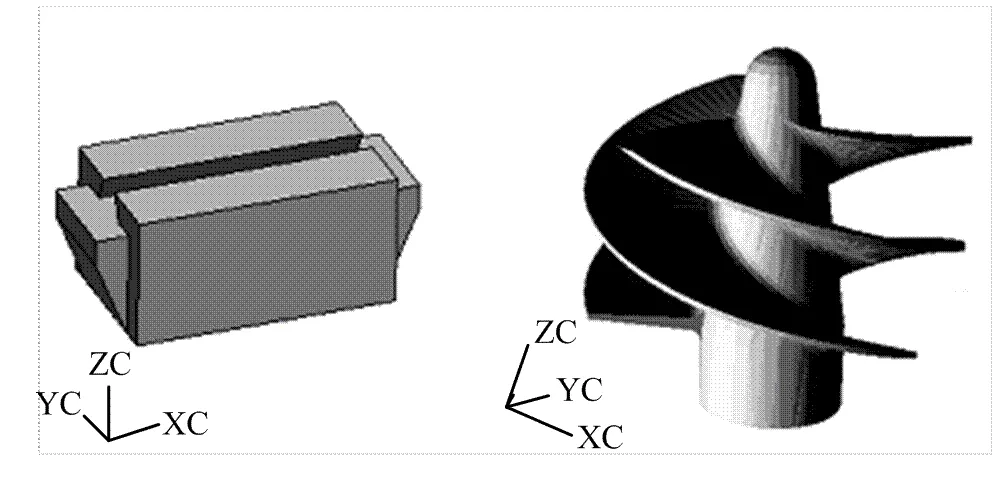
(a) (b)

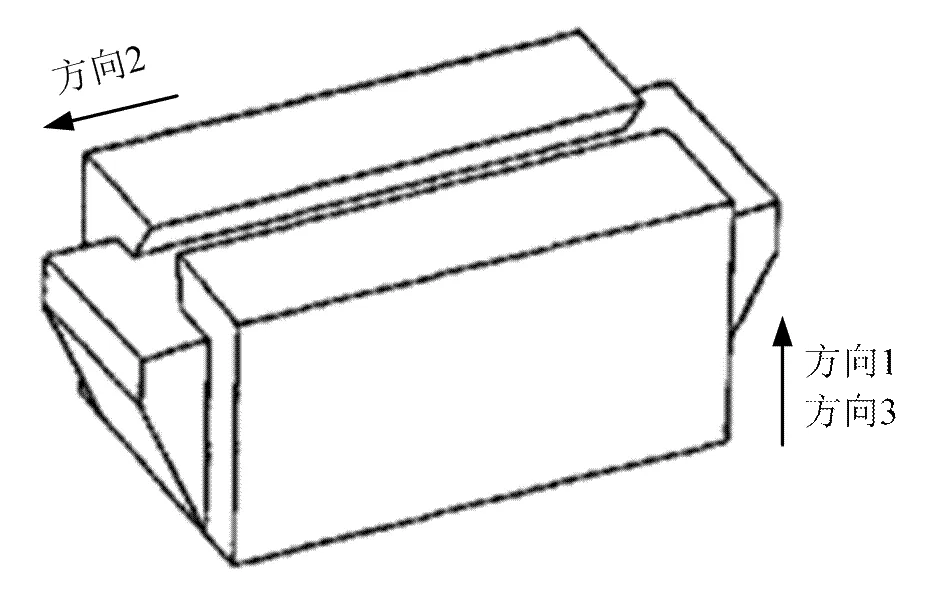
圖3 單目標優化方法求得的導軌滑塊最優制作方向

用NSGA-II多目標優化算法對導軌滑塊模型制作方向的優化計算，得到的Pareto最優結果如表1所示，其中算法的控制參數設置為：種群數100，雜交概率0.9，變異概率0.1，最大進化代數200，切片厚度0.1mm。

表1 導軌滑塊模型的優化計算結果

從表中數據可以看出，用NSGA-II多目標優化算法求得的以減少支撐為目標的最優制作方向與文獻[14-17]中以單目標優化方法得到的相同，而以表面質量和制作時間為目標的最優制作方向與單目標優化方法得到的相差180°。通過查看NSGA-II算法最后得到的優化數據，當＝0°時各優化目標的值為，體積誤差：97.345mm，待支撐面積：10812.3mm，零件制作高度：50mm。由此可見，文獻[14-17]通過單目標優化方法求得的只是一個次優的制作方向，而通過NSGA-II方法求得的才是一個最優的制作方向。這是因為基于Pareto最優原理的多目標優化方法，在優化求解的過程中，可以在保證單一目標最小的情況下，同時具有搜索使其它目標值最小的能力，而通過線性加權法將多目標優化問題轉換成單目標優化問題來求解的方法，則不具備這種搜索能力。從表1中的4號和5號可以看出，通過NSGA-II方法還得到了一個較優的零件制作方向，經過分析可以得出，導軌滑塊模型較優的制作方向實際上只有3個，而這剛好是它的第3個較優的制作方向（即方向）。這表明用NSGA-II方法在對導軌滑塊制作方向的優化計算中不僅比通常單目標優化方法求出了更優的解，而且在一次的優化計算中還得到了它的全部較優解，這也同時表明用多目標遺傳算法NSGA-II方法進行零件制作方向的優化計算是有效的。

根據上述同樣的算法控制參數，用NSGA-II方法對螺旋槳模型制作方向的優化計算得到的Pareto最優目標值的分布分別如圖4所示。圖中每個點都代表著一個較優的制作方向，即3個目標在某一權重系數下的零件最優制作方向。從Pareto最優解集中取得的螺旋槳模型的3個單目標的最優制作方向分別如圖5所示。

對螺旋槳模型按圖5中(a)和(b)兩個制作方向，用光固化三維打印快速成形工藝制做了兩個螺旋槳實物模型（如圖6所示），圖7是螺旋槳實物模型A和B處的局部放大圖。從圖6和圖7中可以看出：通過優化計算得到的按體積誤差最小（即零件表面質量最高）的制作方向制得的零件（圖7(a)所示）的表面質量明顯高于按待支撐面積最小的制作方向制得的零件（圖7 (b)所示）。

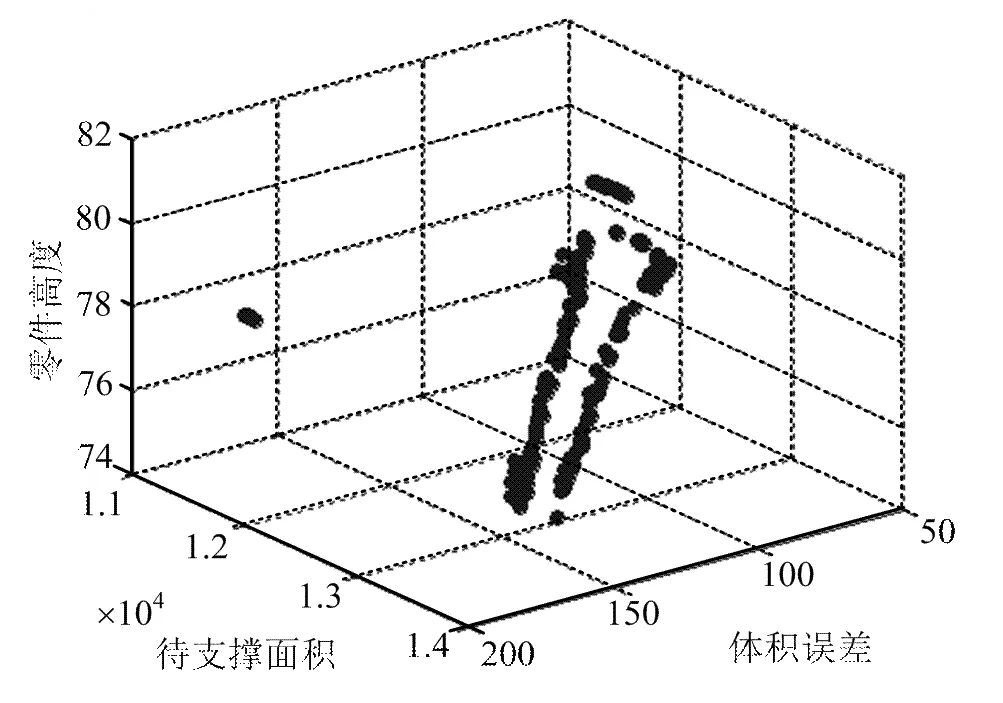
圖4 螺旋槳模型的Pareto最優目標值的分布

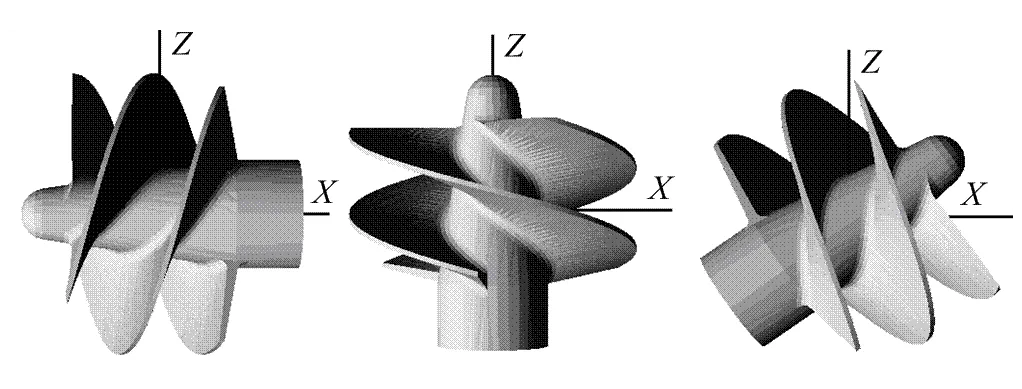
(a) 表面質量最高 (b) 支撐最少 (c) 制作時間最短

(a) 體積誤差最小 (b) 待支撐面積最小

(a) A處局部放大 (b) B處局部放大

4 結 論

零件的制作方向優化是一個多目標優化問題，本文選用了制件表面質量、所需支撐面積和零件制造時間3個指標作為優化目標，分別建立了它們的優化數學模型。采用了基于Pareto最優解的多目標優化遺傳算法NSGA-II進行優化計算，通過與單目標優化方法求得最優結果的對比，表明用多目標優化方法進行零件制作方向的優化計算，不僅可以求出比單目標方法更優的解，而且通過一次優化計算就可得到多個較優的零件制作方向。操作者可以根據實際要求和偏好，從優化計算得到的零件較優制作方向中選取一個合適的方向進行零件制作，以實現零件表面質量、所需支撐和零件的制作時間三者之間的最優組合。

[1] Frank D, Fadel G. Expert system based selection of the preferred direction of build for rapid prototyping [J]. J. Intell. Manuf, 1994, 6(5): 334-339.

[2] Lan P T, Chou S Y, Chen L L, et al. Determining fabrication orientation for rapid prototyping with stereolithography apparatus [J]. Computer Aided Design, 1997, 29(1): 53-62.

[3] Alexander P, Allen S, Dutta D. Part orientation and build cost determination in layered manufacturing [J]. Computer Aided Design, 1998, 30(5): 343-356.

[4] Hong Jun, Wang Wei, Tang Yiping. Part building orientation optimization method in stereolithography [J]. Chinese Journal of Mechanical Engineering, 2006, 19(1): 14-18.

[5] 洪 軍, 武殿梁, 李滌塵, 等. 光固化快速成型中零件制作方向的多目標優化問題研究[J]. 西安交通大學學報, 2001, 35(5): 506-509.

[6] Daekeon Ahn, Hochan Kim, Seokhee Lee. Fabrication direction optimization to minimize post-machining in layered manufacturing [J]. International Journal of Machine Tools & Manufacture, 2007, 47: 593-606.

[7] Rattanawong W, Massod S H, Iovenitti P, A volumetricapproach to part build orientation in rapid prototyping [J]. J. Mater. Process. Technol. 2001, 119: 348-353.

[8] Massod S H, Rattanawong W, Iovenitti P. Part build orientations based on volumetric error in fused deposition modeling [J]. Int. J. Adv. Manuf. Technol., 2000, 16: 162-168.

[9] Massod S H, Rattanawong W, Iovenitti P. A generic algorithm for part orientation system for complex parts in rapid prototyping [J]. J. Mater. Process. Technol., 2003, 139 (1-3): 110-116.

[10] Pandey P M, Reddy N V, Dhande S G. Part deposition orientation studies in layered manufacturing [J]. J. Mater. Process. Technol., 2007, 185: 125-131.

[11] Hong-seok Byun, Kwan H.Lee. Determination of the optimal build direction foe different rapid prototyping processes using multi-criterion decision making [J]. Robotics and Computer-integrated Manufacturing, 2006, 22: 69-80.

[12] Sung-min Hur, Kyung-Hyun Choi, Seok_hee Lee, et al. Determination of fabrication orientation and packing in SLS process [J]. J. Mater. Process. Technol., 2001, 112: 236-243.

[13] 趙吉賓, 何利英, 劉偉軍, 等. 快速成型制造中零件制作方向的優化研究[J]. 計算機輔助設計與圖形學學報, 2006, 18(3): 456-463.

[14] Xu F, Loh H T, Wong Y S. Considerations and selection of optimal orientation for different rapid prototyping system [J]. Rapid Prototyping Journal, 1999, 5(2): 54-60.

[15] Cheng W, Fuh J Y H, Nee A Y C, et al. Multi- objective optimization of part-building orientation in stereolithography [J]. Rapid Prototyping Journal, 1995, 1(4): 12-23.

[16] 董 濤, 章維一, 王春暉, 等. 快速成型制造中的零件分層方向優化新技術[J]. 計算機工程與應用, 2003, (1): 45-48.

[17] 張立強, 羅逸葦, 王斌修. 基于遺傳算法的RP 分層方向優化設計[J]. 電加工與模具, 2003, (6): 35-38.

[18] 鄭向偉, 劉 弘. 多目標進化算法研究進展[J]. 計算機科學, 2007, 34(7): 187-192.

[19] 王安麟, 朱學軍, 張惠僑. Pareto多目標遺傳算法及其在機械健壯設計中的應用[J]. 機械設計與研究, 2000, (1): 10-13.

[20] 李梅娟, 陳雪波. Pareto 遺傳算法在貨位配置中的應用研究[J]. 控制工程, 2006, 13(2): 138-141.

[21] Kalyanmoy Deb, Amrit Pratap, Sameer Agarwal, et al. A fast and elitist multi-objective genetic algorithm:NSGA-II [J]. IEEE Transactions on Evolutionary Computation, 2002, 6(2): 182-197.

Part Building Orientation Optimization Based on Pareto Optimal Solutions

LIU Hou-cai, LIAO Yan-chun

( College of Electromechanical Engineering, Hunan University of Science and Technology, Xiangtan Hunan 411201, China )

The effect of part building orientation on the part’s surface quality, the needed supporting area and building time is analyzed in the processing of rapid prototyping, and their optimizing models are established. The multi-objective optimizing generic algorithm of NSGA-II based on Pareto optimal solutions are used to seek the optimum solutions. Compared with the results gained by the single-objective optimizing way, it is shown that not only the better solution is gained but also many Pareto optimal solutions can be gained in one optimizing computing by NSGA-II.

computer application; rapid prototyping; multi-objective optimizing; part building orientation;Pareto optimal solutions

TP 391

A

1003-0158(2011)01-0157-06

2009-07-13

湖南省教育廳科研資助項目（09C397）；湖南省自然科學基金重點資助項目（09JJ3093）

劉厚才（1975-），男，湖北廣水人，博士，主要研究方向為快速成型與快速制模。