基于參數(shù)樣條插值的同坡曲面構(gòu)造方法

李軍成

?

基于參數(shù)樣條插值的同坡曲面構(gòu)造方法

李軍成

（湖南人文科技學(xué)院數(shù)學(xué)系，湖南婁底 417000）

傳統(tǒng)的同坡曲面構(gòu)造方法都是在導(dǎo)線方程為已知的前提下進(jìn)行的。然而在實(shí)際工程中，導(dǎo)線方程往往是很難得到的，只能通過(guò)測(cè)量得知導(dǎo)線通過(guò)一列數(shù)據(jù)點(diǎn)。針對(duì)這一問(wèn)題，給出了一種實(shí)際工程中同坡曲面的構(gòu)造方法，該法首先根據(jù)測(cè)量數(shù)據(jù)點(diǎn)，利用三次參數(shù)樣條曲線插值方法構(gòu)造出同坡曲面的導(dǎo)線方程，然后再?gòu)耐虑娴男纬稍砣胧纸⑵鋮?shù)方程，最后通過(guò)實(shí)例表明該方法是可行有效的。

計(jì)算機(jī)應(yīng)用；同坡曲面；參數(shù)樣條曲線；插值；包絡(luò)面

同坡曲面是水利、土建及其它工程設(shè)計(jì)中一種常見(jiàn)的特殊坡面，它在工程中有著非常重要的作用，因此建立同坡曲面的方程是非常有理論與實(shí)際意義的。文獻(xiàn)[1]從同坡曲面的特性入手，提出了建立這類(lèi)坡面數(shù)學(xué)模型的方法；文獻(xiàn)[2]通過(guò)對(duì)遞推圓弧樣條曲線的研究，探討了構(gòu)造同坡曲面等高線的方法和相關(guān)問(wèn)題；文獻(xiàn)[3-4]則對(duì)同坡曲面的形成作了分析，給出了更為一般的同坡曲面的方程等。這些文獻(xiàn)雖然都從某種角度討論了同坡曲面的方程，但都是以同坡曲面的導(dǎo)線方程有準(zhǔn)確表達(dá)式為前提。事實(shí)上，在實(shí)際工程中，同坡曲面的導(dǎo)線方程的準(zhǔn)確表達(dá)式往往是很難得到的，而只能通過(guò)測(cè)量得到導(dǎo)線上的一組數(shù)據(jù)點(diǎn)，為解決這個(gè)問(wèn)題，本文利用三次參數(shù)曲線的構(gòu)造方法，首先構(gòu)造出插值于這些數(shù)據(jù)點(diǎn)的導(dǎo)線參數(shù)方程，再?gòu)耐虑娴男纬稍砣胧纸⑼虑娴姆匠蹋苑蠈?shí)際工程的需要。

1 同坡曲面的形成原理[5]

正圓錐的軸線始終垂直于水平面，錐面上所有素線對(duì)水平面的傾角都相等，當(dāng)直母線沿著一條空間曲導(dǎo)線移動(dòng)，母線對(duì)水平面的傾角始終保持不變時(shí)，所形成的曲面稱(chēng)為同坡曲面。

如圖1所示，轉(zhuǎn)彎斜坡道邊是一條空間導(dǎo)線，過(guò)所作的同坡曲面可以看成是公切于一組正圓錐面的包絡(luò)面，且這些正圓錐頂點(diǎn)都在導(dǎo)線上，素線與水平面的傾角都相等。顯然，同坡曲面上的每條素線（也稱(chēng)為坡度線）都是這個(gè)曲面與圓錐面的切線，也為圓錐面上的母線。也就是說(shuō)，同坡曲面上所有坡度線與水平面的傾角都相等。若用水平面截割同坡曲面和圓錐面，截得同坡曲面上的等高線（也稱(chēng)同坡曲線）和圓錐面上的等高線（水平圓）一定相切，且切點(diǎn)必在坡度線上。

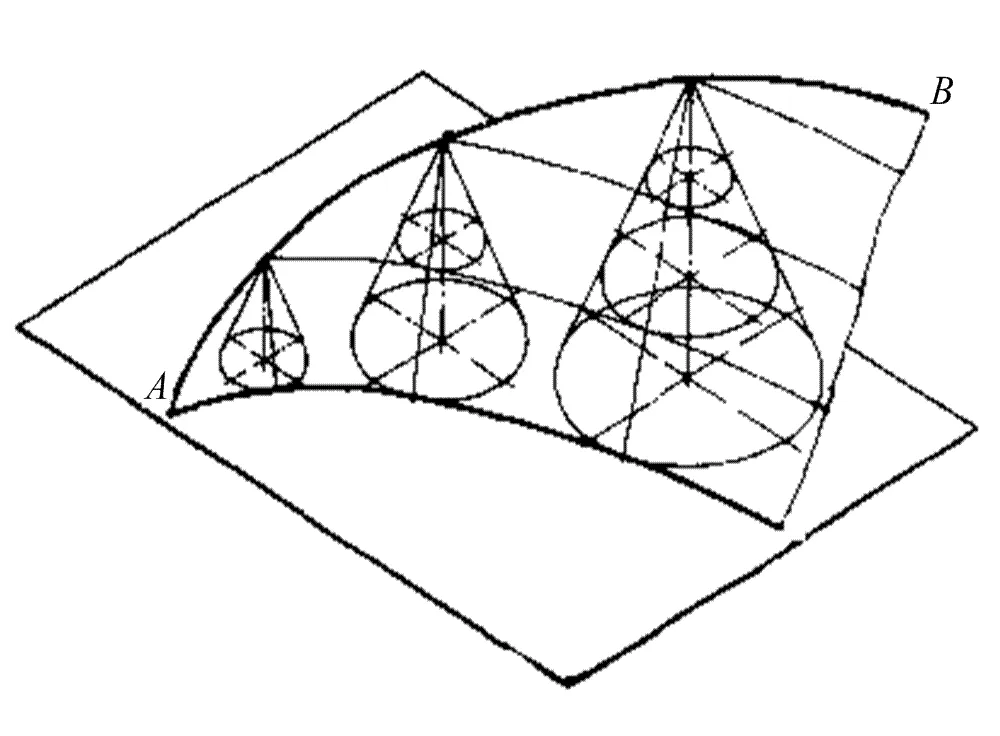
圖1 同坡曲面的形成原理

2 同坡曲面的構(gòu)造

2.1 導(dǎo)線的參數(shù)方程

要建立同坡曲面的參數(shù)方程，首先必需知道導(dǎo)線的參數(shù)方程。實(shí)際工程中，導(dǎo)線的方程往往很難得到，只能通過(guò)測(cè)量得到導(dǎo)線上的一組數(shù)據(jù)點(diǎn)，其中,。此時(shí)可以通過(guò)參數(shù)樣條插值方法構(gòu)造出通過(guò)這些數(shù)據(jù)點(diǎn)的導(dǎo)線方程。

當(dāng)所測(cè)數(shù)據(jù)點(diǎn)分布比較均勻時(shí)，可用Ferguson方法構(gòu)造插值曲線，其表達(dá)式可寫(xiě)為

但當(dāng)所測(cè)數(shù)據(jù)點(diǎn)分布不均時(shí)，用Ferguson方法構(gòu)造的插值曲線會(huì)出現(xiàn)波動(dòng)，此時(shí)可以應(yīng)用累加弦長(zhǎng)參數(shù)樣條曲線方法構(gòu)造插值曲線。

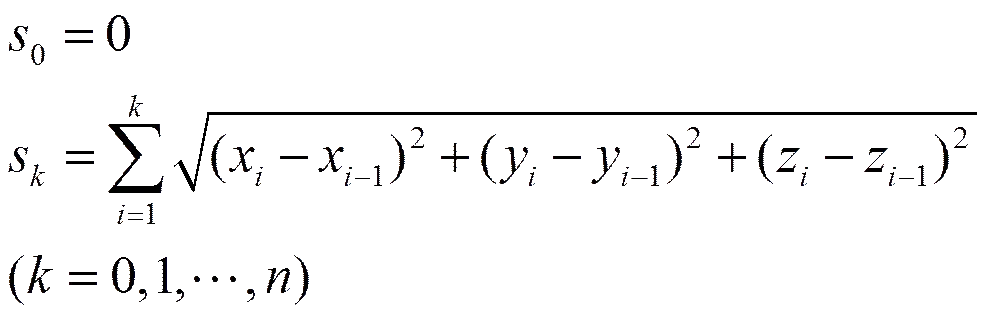
參數(shù)方程(2)可作為同坡曲面的導(dǎo)線方程。需要說(shuō)明的是，在構(gòu)造導(dǎo)線的參數(shù)方程時(shí)，也可采用B-樣條方法構(gòu)造插值曲線。若所測(cè)數(shù)據(jù)點(diǎn)分布均勻時(shí)，可用均勻B-樣條插值；而當(dāng)所測(cè)數(shù)據(jù)點(diǎn)分布不勻時(shí)，則可用非均勻B-樣條插值。這里由于篇幅有限，不再贅述。

導(dǎo)線方程建立后，由同坡曲面的形成原理可知，要得到同坡曲面的方程，需首先建立一組正圓錐面的方程，再求出公于該組圓錐面的包絡(luò)面即可。

2.2 正圓錐面的參數(shù)方程

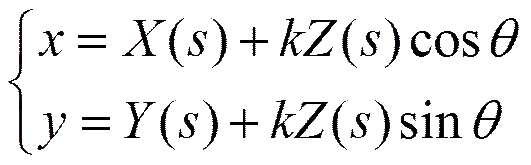
（3）

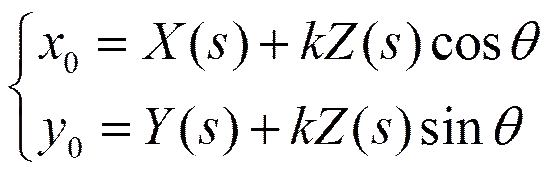
（5）

2.3 同坡曲面的參數(shù)方程

由于同坡曲面可以看成是公切于一組正圓錐面的包絡(luò)面，因此，中的每一個(gè)圓錐都有一條直母線在同坡曲面上，例如在上由，決定的直母線在上；在上有，決定的直母線在上，……，在上由，決定的直母線也在上。由此可知與之間必存在某種規(guī)律，不妨設(shè)。于是，的參數(shù)方程可寫(xiě)為

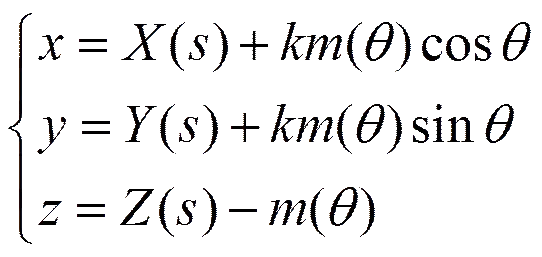
另一方面，根據(jù)包絡(luò)面的定義可知，與沿接觸線相切，于是它們?cè)谏嫌泄卜ㄏ蛄浚囱厣厦奎c(diǎn)的法向量也為沿上每點(diǎn)的法向量。

，

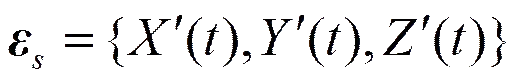
于是有

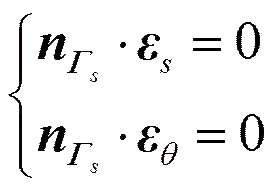
上式計(jì)算整理得

（7）

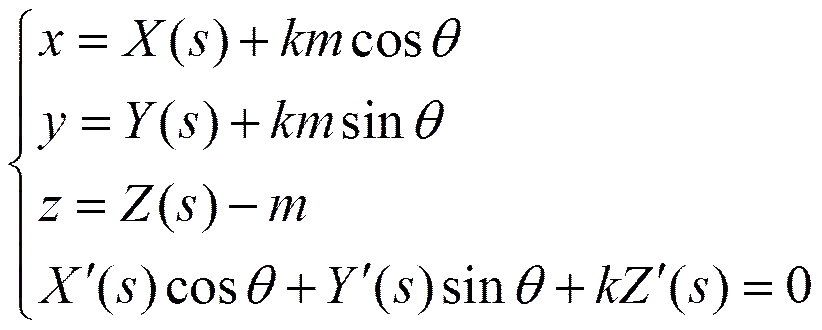
3 應(yīng)用實(shí)例

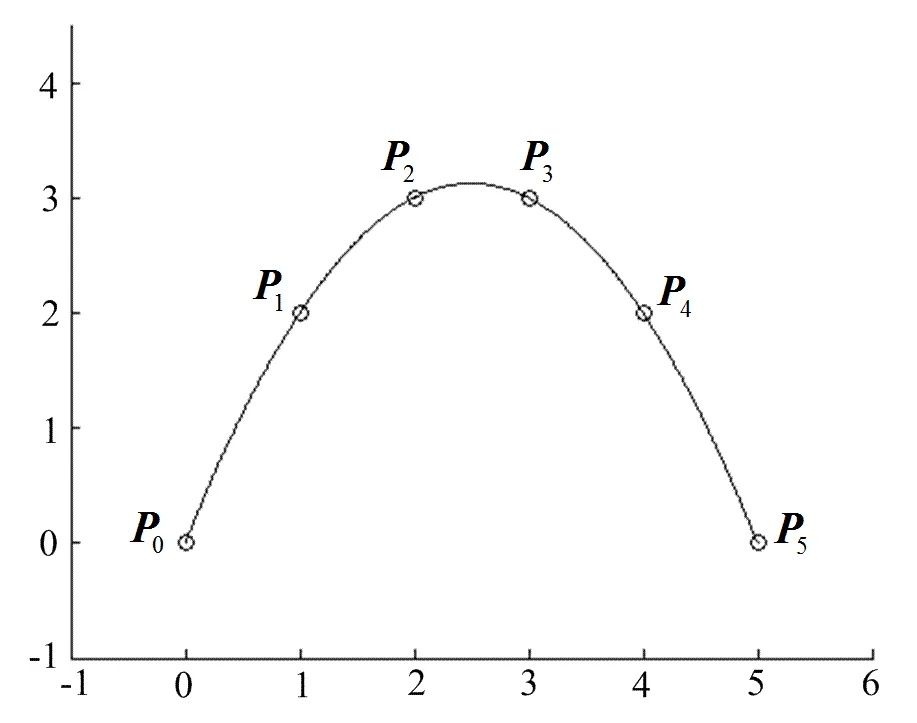
圖2 插值于各數(shù)據(jù)點(diǎn)的導(dǎo)線

圖3 導(dǎo)線為插值曲線時(shí)的同坡曲面

4 結(jié) 論

本文根據(jù)實(shí)際工程的需要，當(dāng)同坡曲面的導(dǎo)線方程沒(méi)有準(zhǔn)確表達(dá)式時(shí)，首先利用三次參數(shù)樣條插值方法構(gòu)造出插值于各測(cè)量數(shù)據(jù)點(diǎn)的導(dǎo)線方程，然后再?gòu)耐虑娴男纬稍砣胧纸⑼虑娴姆匠獭Ｐ枰赋龅氖牵?dāng)所的數(shù)據(jù)點(diǎn)分布比較均勻時(shí)，可用三次Ferguson曲線插值構(gòu)造導(dǎo)線效果較好；但當(dāng)所測(cè)數(shù)據(jù)點(diǎn)分布不均時(shí)，采用累加弦長(zhǎng)三次參數(shù)樣條插值曲線來(lái)構(gòu)造導(dǎo)線會(huì)達(dá)到滿意的效果。

[1] 陳永喜. 同坡曲面的數(shù)學(xué)模型及計(jì)算機(jī)輔助幾何設(shè)計(jì)[J]. 工程圖學(xué)學(xué)報(bào), 1998,(1): 48-54.

[2] 屈振生. 圓弧樣條曲線在道路工程圖中的應(yīng)用[J]. 遼寧工程技術(shù)大學(xué)學(xué)報(bào)(自然科學(xué)版), 2000, 19(6): 622-625.

[3] Hu jianguo, Chen yueping. Mathematical model of the identical slope surface [J]. Wuhan University Journal of Natural Sciences, 2002, 7(1): 54-58.

[4] 劉青科, 毛 君. 同坡曲面的方程及其在彎斜路面邊坡設(shè)計(jì)和繪圖中的應(yīng)用[J]. 武漢大學(xué)學(xué)報(bào)(工學(xué)版), 2006, 39(4): 111-114.

[5] 方 慶, 徐約素, 等. 畫(huà)法幾何及水利工程制圖(第2版)[M]. 北京: 高等教育出版社, 1978. 178-180.

[6] Ferguson J C. Multivariable curve interpolation [J]. Journal ACM, 1964, 11(2): 221-228.

[7] 朱心雄, 等. 自由曲線曲面造型技術(shù)[M]. 北京: 科學(xué)出版社, 2000. 44-145.

[8] 蘇步青, 劉鼎元. 計(jì)算幾何[M]. 上海: 上海科學(xué)技術(shù)出版社, 1981. 78-88.

[9] 復(fù)旦大學(xué)數(shù)學(xué)系《曲線與曲面》編寫(xiě)組. 曲線與曲面[M]. 北京: 科學(xué)出版社, 1977. 162-167.

A Method for Constructing Identical Slope Surface Based on Parametric Spline Interpolation

LI Jun-cheng

( Department of Mathematics, Hunan Institute of Humanities, Science and Technology, Loudi Hunan 417000, China )

The traditional method for constructing identical slope surface is under the premise that exact expression of lead curve is known. But in practical engineering, the exact expression of lead curve is hard to obtain, and only some measured data points of the lead curve are given. For solving that problem, a method of constructing the identical slope surface in engineering is presented in this paper. Firstly, cubic parametric spline interpolation curve is constructed according to the measured data points, which is regarded as the lead curve. Then, the parametric equation of identical slope gradient surface is constructed based on the forming principle of that surface. Lastly, an example is presented to show the method is feasible and effectual.

computer application; identical slope surface; parametric spline curve; interpolation; envelope surface

O 182；TP 391

A

1003-0158(2011)01-0026-05

2009-07-03

李軍成（1982-），男，湖北漢川人，講師，碩士，主要研究方向?yàn)橛?jì)算機(jī)輔助幾何設(shè)計(jì)。