連續梁橋上CRTSⅡ型板式無砟軌道伸縮附加作用計算分析

代永波

(武漢鐵路局，武漢 430000)

CRTSⅡ型板式無砟軌道選用了在短橋上連續鋪設軌道板的優點，取消了軌道板在長橋上分塊。橋上軌道結構通過梁面鋪設“兩布一膜”滑動層、橋梁固定支座上方梁面設置抗剪齒槽和錨固筋、臺后設置端刺和摩擦板等技術措施，實現了軌道結構跨梁縫連續鋪設，軌道結構整體性和縱向連續性好[1-4]。

1 計算模型及參數

橋上CRTSⅡ型板式無砟軌道與橋梁間的相互作用與普通橋上無縫線路的梁、軌相互作用既有共性又存在差異。橋梁伸縮而引起的鋼軌縱向附加力、軌道板和底座板的縱向附加力為伸縮力，伸縮力是梁、軌相互作用中一項重要計算荷載。

橋上CRTSⅡ型板式無砟軌道與橋梁的伸縮附加作用原理可以表述為:在梁體溫度變化作用下，橋梁與軌道結構之間產生相對位移，這種相對位移通過滑動層摩擦、剪力齒槽、鋼軌扣件等梁軌間相互約束，使軌道結構受到縱向力的作用。這些力同時又反作用于橋跨和固定支座，使橋梁墩臺產生彈性變形，最終橋梁與軌道形成一個相互作用的力學平衡體系。

1.1 計算模型

橋上縱連板式無砟軌道是一個非常復雜的力學系統，要進行完全精確的模擬是十分困難的，其計算模型的建立，應滿足既能在總體上較為真實地反映結構的受力情況，同時也能考慮到計算的方便和可靠性，在滿足工程精度需要的前提下，進行適當的簡化。現對全橋縱連板式無砟軌道的線—板—橋—墩一體化模型作如下假定:①鋼軌為縱向連續長梁，其拉、壓剛度相等，且為常量;②鋼軌和軌道板間產生縱向相對位移，二者通過扣件相互作用，扣件阻力與鋼軌、軌道板的相對位移為非線性關系;③假設橋梁固定支座能完全阻止梁的伸縮，阻止橋梁縱向變形的剛度就為墩臺頂縱向水平剛度，活動支座抵抗伸縮的阻力可忽略不計;④底座板與橋梁間產生縱向相對位移，二者通過滑動層與限位機構進行縱向相互作用，滑動層的摩擦阻力與二者間的相對位移為非線性關系，固結機構縱向作用力與二者間的相對位移為線性關系;⑤假定瀝青砂漿對軌道板和底座板提供非線性阻力作用，軌道板和底座板間的非線性阻力隨著二者的相對位移呈非線性變化，非線性阻力的最大值依據相關試驗數據確定;⑥底座板與端刺和摩擦板產生縱向相互作用，端刺縱向剛度為線性的，摩擦板與底座板的摩擦阻力為非線性。根據以上假定，建立如圖1所示的線—板—橋—墩空間一體化縱向力計算模型。

1.2 計算參數選取

針對高速鐵路某一特殊工點，橋梁跨數較多，選取其中間部分簡支梁和連續梁建立有限元模型進行計算，橋梁結構的參數如表1所示。

鋼軌扣件縱向阻力采用非線性彈簧模擬，有載 r=60 kN/m·線;無載 r=30 kN/m·線，極限位移 u0=0.5 mm;底座板與橋梁之間“兩布一膜”采用非線性彈簧模擬，縱向摩擦系數取0.3，滑動極限位移0.5 mm。鋼軌為60 kg/m鋼軌，橋梁的截面面積8.962 m2，豎向抗彎慣性矩11.0 m4，橫向抗彎慣性矩84.73 m4，混凝土彈性模量3.55×104MPa;梁體降溫按15℃計算。

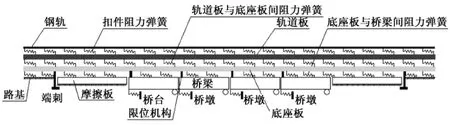
圖1 線—板—橋—墩縱向力計算模型

表1 橋梁結構參數

2 伸縮附加作用計算

2.1 伸縮位移計算

從降溫工況下梁體縱向位移曲線圖2(圖中橫坐標原點為模型小里程端起點，圖3至圖7同)可以看出，各跨梁體位移曲線主要受自身溫度跨度大小控制，溫度跨度越大梁體的伸縮位移越大，32 m等跨度簡支梁的位移曲線大致相同。

軌道各結構層的總體位移特征如圖3所示。由位移特征圖形可以發現，軌道板、底座板的位移特征與鋼軌的位移特征相似。受連續梁大溫度跨度的影響，在連續梁上的軌道結構伸縮位移與梁伸縮方向相同，最大位移量出現在連續梁與簡支梁接縫附近，鋼軌最大位移為0.43 mm，軌道板和底座板的最大位移為0.45 mm，并且在連續梁中部也存在位移零點。

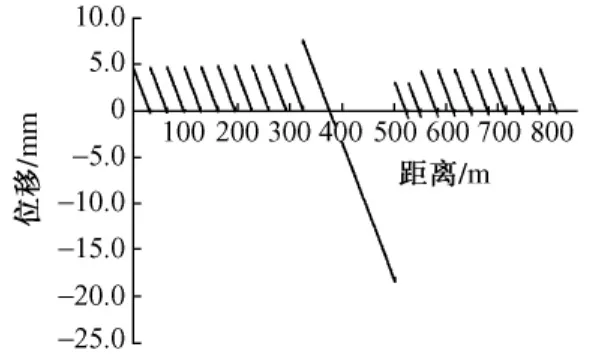
圖2 橋梁位移

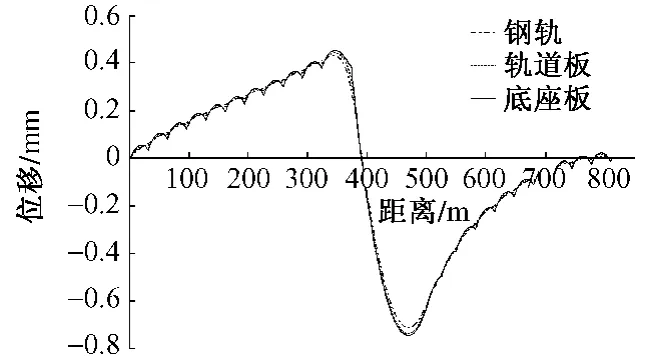
圖3 軌道各結構層位移

鋼軌相對于軌道板位移及底座板相對于梁面的位移分別如圖4和圖5所示，可以看出，梁體降溫15℃時，大部分區域內梁面與底座板間的相對位移差超過0.5 mm，即兩者處于滑動狀態;而軌道板和鋼軌間的相對位移遠小于0.5 mm，扣件阻力處于彈性范圍。

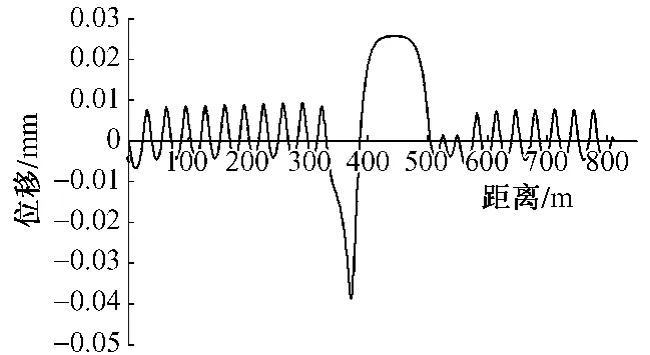
圖4 鋼軌相對于軌道板位移

圖5 底座板相對于梁面位移

2.2 伸縮附加力計算

軌道各結構層的縱向力特征如圖6、圖7所示。由鋼軌縱向力特征圖形可以看出，受中部連續梁大伸縮跨影響，連續梁上鋼軌受到較大的壓力，簡支梁上部區域鋼軌受拉。軌道板、底座板的縱向受力特征與鋼軌大致相同。在連續梁固定支座上方附近區域，軌道結構受到的伸縮附加力最大，鋼軌受到的最大伸縮壓力為28.4 kN，軌道板最大伸縮壓力為295.1 kN，底座板最大伸縮壓力為580.1 kN。

圖6 鋼軌縱向力

圖7 軌道板及底座板縱向力

單線剪力齒槽受力如圖8所示。最大剪力出現在連續梁固定支座，為591 kN，且由于連續梁的固定支座布置在靠近小里程端的268#號墩上，與簡支梁固定支座布置在大里程端不同，所以連續梁上剪力齒槽受力方向與簡支梁上的相反。另外還可以看出簡支梁跨剪力齒槽主要與溫度跨度大小有關，等跨的32 m簡支梁上剪力齒槽受力較為均勻，在205～291 kN之間;而25 m和24 m跨度的簡支梁上剪力齒槽受力為165 kN左右。橋墩受力如圖9所示。可以看出，連續梁固定支座所在的268#號橋墩所受的縱向力最大為255 kN，另外靠近大里程端簡支梁的橋墩受力較小里程端簡支梁橋墩受力要大。

圖8 單線剪力齒槽縱向力

圖9 橋墩受力

3 伸縮附加作用影響因素分析

3.1 滑動層摩擦系數影響分析

滑動層對橋上縱連板式結構起著非常重要的作用，但在運營過程中，其摩擦系數會發生變化，有可能發生滑動層失效的情況，而且滑動層一旦失效，將無法修復，因此在設計中必須要考慮到滑動層摩擦系數對軌道結構的影響。本節將滑動層摩擦系數分別取為0，0.15，0.30，0.45，0.60，計算 5 種工況下梁軌相互作用的伸縮特性。由圖10可以看出，隨著底座板和橋梁之間滑動層的摩擦系數的增大，底座板相對橋梁的位移值不斷減小。鋼軌、軌道板、底座板的縱向力隨滑動層摩擦系數的增加而不斷增大(如圖11—圖 13所示)，由圖14、圖15也可看出剪力齒槽最大剪力及連續梁固定支座所在橋墩的受力變化趨勢也有相同的規律。

總的來看，在相同梁體伸縮量的條件下，摩擦系數的大小直接反應了梁體和軌道間相互作用力。隨著運營時間的延長，滑動層若出現破損，將導致其摩擦系數增大，從安全角度考慮，宜采用其在極限狀態下的最大摩擦系數進行線—橋系統的設計檢算，同時應規定橋面滑動層在服役期內的最大摩擦系數不宜超過一定的限值。

3.2 底座板剛度折減影響分析

軌道結構由鋼軌、軌道板、底座混凝土板和CA砂漿墊層組成，隨著溫度變化和外部荷載的作用，底座板必然會出現開裂現象，使底座板抗拉剛度減小，最終影響結構受力。在此，主要討論底座板在開裂狀態下軌道和橋梁各結構的受力變化情況，為深入研究縱連板式橋上無砟軌道的設計檢算提供計算依據。

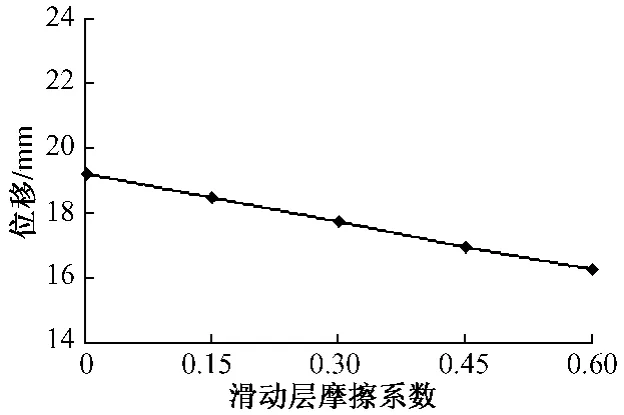
圖10 底座板相對橋梁最大位移隨摩擦系數變化

圖11 鋼軌縱向力隨摩擦系數變化

圖12 軌道板縱向力隨摩擦系數變化

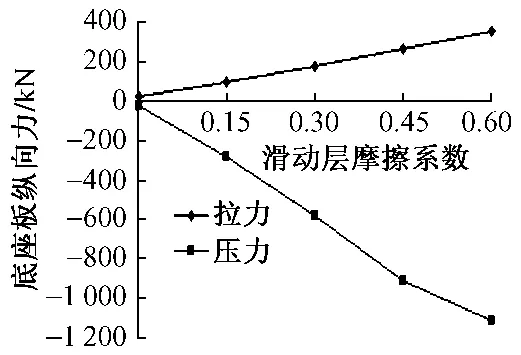
圖13 底座板縱向力隨摩擦系數變化

圖14 剪力齒槽最大剪力隨摩擦系數變化

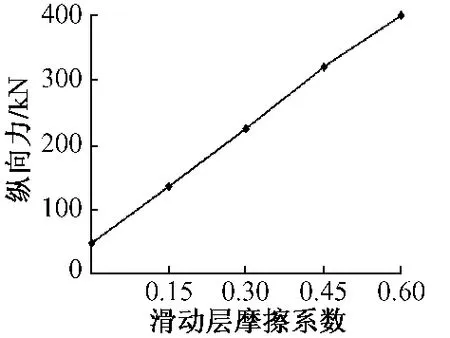
圖15 連續梁橋墩受力隨摩擦系數變化

本節在考慮溫度荷載作用下底座板剛度對結構受力的影響時，取底座板全線伸縮剛度為全截面剛度的20%，40%，60%，80%和100%，計算5種工況下的橋上縱連板式無砟軌道的伸縮特性。

由圖16可以看出，底座板軸向剛度的增大，底座板相對橋梁的位移值有所增加。鋼軌、軌道板、底座板的縱向力隨著底座板縱向剛度折減的變化規律分別如圖17—圖19所示，隨著底座板軸向剛度的增加，軌道板縱向力下降，但是底座板所受縱向力則呈增大趨勢。這主要是由于在降溫時，鋪設完成的縱連底座板，由于伸縮剛度較大，在最大溫降及收縮徐變作用下承受相當大的縱向力，會導致混凝土開裂，隨著底座板裂縫的增多及加寬，底座板縱向剛度減小，其所承受的縱向力也逐漸減小，最終達到受力與開裂的平衡。

由圖20可以看出，剪力齒槽最大剪力隨底座板剛度的增加而逐漸增大，但增大幅度不斷減小;而圖21顯示連續梁固定支座橋墩所受的縱向力隨著底座板剛度的增加而逐漸減小。

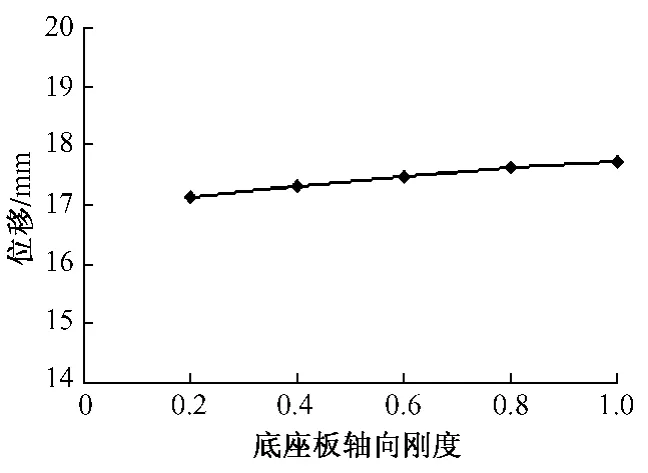
圖16 底座板相對橋梁最大位移隨底座板剛度變化

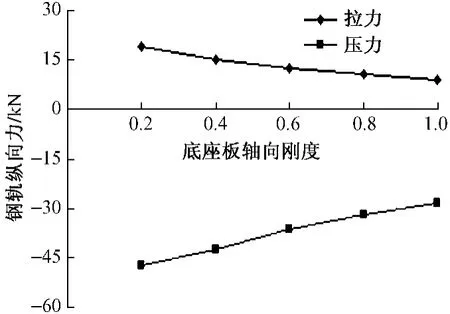
圖17 鋼軌縱向力隨底座板剛度變化

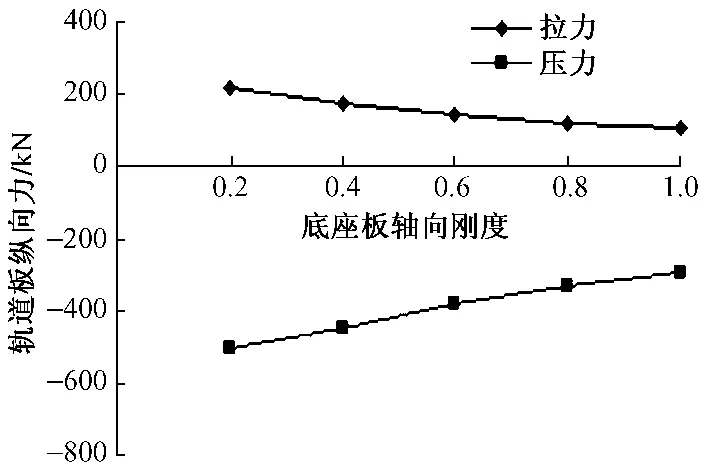
圖18 軌道板縱向力隨底座板剛度變化

圖20 剪力齒槽最大剪力隨底座板剛度變化

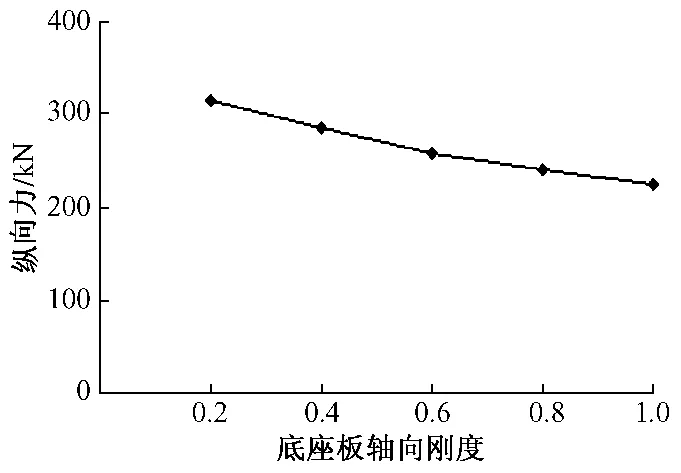
圖21 連續梁橋墩受力隨底座板剛度變化

4 結論

由以上計算結果及分析，可以得出如下結論:

1)由于橋上底座板和軌道板縱連，相當于橋上無縫線路的固定區，其縱向受力及變形特征與鋼軌的相似，不過底座板受滑動層摩擦及剪力齒槽的傳力作用，其位移特征受梁跨影響相對明顯。整體上看，底座板與橋梁之間設置“兩布一膜”的隔離層，減弱了橋梁的伸縮對軌道結構的影響，軌道結構受梁軌相互作用產生的軸力和位移量值不大;

2)扣件縱向阻力大于底座板和梁面間“兩布一膜”隔離層的最大靜摩擦力，因此滑移面首先出現在梁面和底座板之間;分析表明，各種工況下鋼軌和軌道板間相對位移小于滑移位移，扣件系統受力處于彈性范圍;

3)梁軌相互作用過程中，軌道板與底座板之間相對位移較小，基本為同步變形，即砂漿調整層使得底座板和軌道板協同受力;

4)底座板和橋梁之間滑動層的摩擦系數直接影響橋梁伸縮作用的大小，隨著摩擦系數的增大，底座板相對橋梁的位移值不斷減小，而軌道結構各層的最大軸力、剪力齒槽最大剪力及連續梁固定支座所在橋墩的受力不斷增大;

5)在伸縮工況下，隨底座板軸向剛度的增大，底座板相對橋梁的位移值有所增加，軌道板縱向力下降，但是底座板所受縱向力則呈增大趨勢。對于縱連的底座板，在最大溫降及收縮徐變作用下承受相當大的縱向力，會導致混凝土開裂，隨著底座板裂縫的增多及加寬，底座板縱向剛度減小，其所承受的縱向力也逐漸減小，最終達到受力與開裂的平衡。隨底座板剛度的增加，剪力齒槽最大剪力逐漸增大，但連續梁固定支座橋墩所受的縱向力逐漸減小。

[1]何華武.無砟軌道技術[M].北京:中國鐵道出版社，2005.

[2]徐慶元，張旭久.高速鐵路博格縱連板橋上無砟軌道縱向力學特性[J].中南大學學報(自然科學版)，2009，40(2):527-531.

[3]包進榮，陳小平，王平.橋上CRTSⅡ型板式無砟軌道計算軟件開發及應用[J].鐵道建筑，2011(1):97-99.

[4]宋楊，王平，張國棟，等.滑動層對橋上 CRTSⅡ型板式無砟軌道無縫道岔群的受力影響[J].鐵道建筑，2011(11):108-111.