基于誤差預報的控制系統綜合性能評價

王智勇 王勇慧 白 波

(中國核電工程有限公司河北分公司1，河北 石家莊 050011;河北大學保衛處2，河北 保定 071002;河北大學工商學院3，河北 保定 071002)

0 引言

在工業生產過程中，很多控制系統的性能會隨著時間的推移而退化，導致生產效率降低，造成資源浪費，增加不合格產品。

Harris提出用最小方差控制(minimum variance control，MVC)作為性能指標，對單輸入單輸出系統進行評價。在此基礎上，眾多學者針對前饋/反饋、單變量/多變量控制系統提出了許多評價基準［1-2］。Folake Olaleye、Biao Huang等人對多擾動動態下的PID控制器構造了一種帶加權的綜合性能評價函數，得到系統對各擾動動態的最佳折中性能［3-4］。Rachid A.Ghraizid等人通過計算控制器的預測誤差和殘差對控制系統進行性能監控［5］。Ari Ingimundarson、Tore H?gglund采用擴展預測步長的方法，選擇實際控制器所能達到的最優控制性能下限作為評價的基準［6］。N.F.Thornhill等人基于 MVC 的方法提出了控制系統設定值跟蹤的性能評價方法［7-8］。

上述方法都只針對單一模式的性能指標或動態性能評價控制系統的運行，但在多數情況下，控制系統的隨機性性能良好，確定性性能卻不理想，反之亦然。對此，本文針對多操作模式的過程控制系統，基于誤差預報技術，提取控制系統可達到的最小方差，實現對控制系統的綜合性能評價。

1 控制系統性能分析

1.1 預備知識

設{ωk}為平穩、零均值序列，則它可以用一系列白噪聲序列{ak}的自回歸滑動平均模型(ARMA模型)表示［9］，即:

式中:{Gj}為脈沖傳遞函數的系數序列。

式(1)又可以表示為:

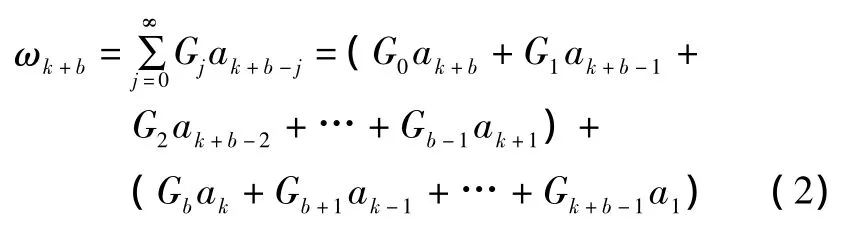
由于{ak}為白噪聲序列，在k時刻不能依據已有ak、ak-1、ak-2、…、a1的值去預測未來 ak+1、ak+2、…、ak+b的值，即{ak}的未來值是不可預測的。因此，式(2)中第一個括號內的各項是無法計算的;而對于第二個括號內的各項，由于在 k時刻，所有的 ak、ak-1、ak-2、…、a1都已確定，因此是可計算的，即時間序列{ωk}在k時刻及其以前的歷史數據 ωk、ωk-1、ωk-2、…是已知的。由已知的歷史數據對(k+b)時刻的數據ωk+b進行預測，稱為時間序列{ωk}的第b步預報值，記作(b)，其中b為預報步長。

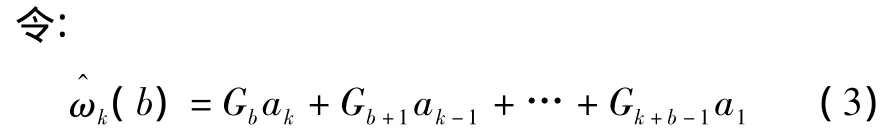
式(3)中，被選定的系數序列{Gj}應使預報誤差的均方值達到最小，預報誤差的均方值如式(4)所示。

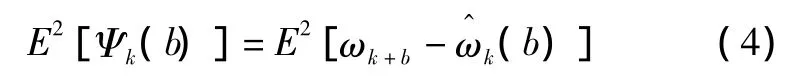
因為{ωk}是零均值序列，所以:

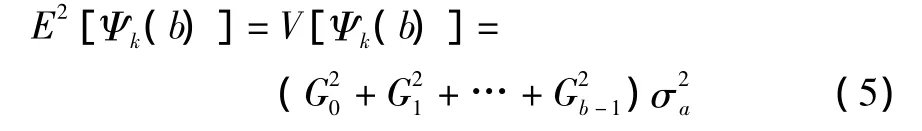
可以證明，若b等于控制系統的時間延遲d，則式(5)等號右邊部分恰好為最小方差控制下的“反饋控制不變項”。式(5)選擇合適的b值，即可得到控制系統的最小方差。此外，對于平穩、零均值序列，只要有有限個歷史數據，就能遞推求得關于該序列任意步的平穩最小方差預報。本文選取m個歷史數據，可得:

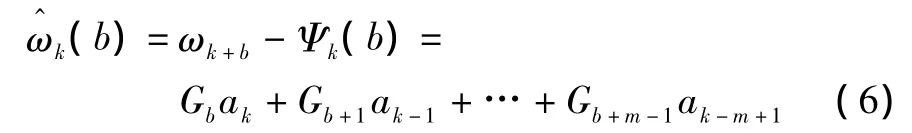
預報值的方差為:

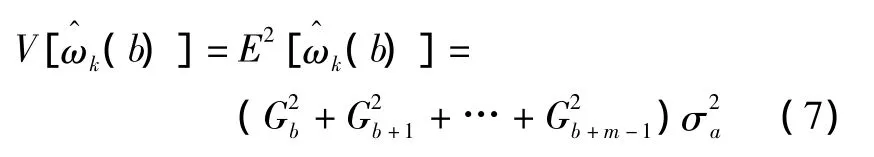
1.2 誤差預報

典型單輸入單輸出控制系統如圖1所示。

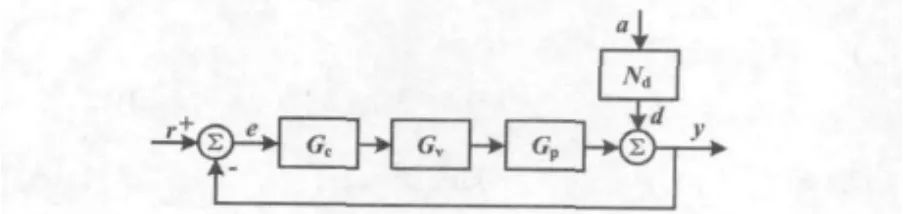
圖1 典型單輸入單輸出控制系統Fig.1 Typical SISO control system

對于如圖1所示的典型單輸入單輸出系統，定義系統誤差:

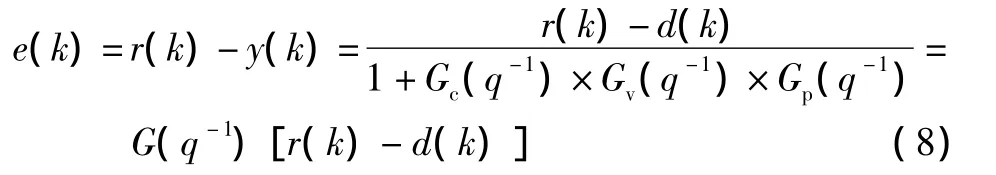
式中:r(k)為設定值;y(k)為過程輸出值;Gc為控制器傳輸函數;Gv為控制閥傳輸函數;Gp為過程傳輸函數;Nd為擾動傳輸函數;a為擾動變量。此處擾動d=Nda為各擾動動態的通式，表示在不同操作模式下具有的不同擾動動態。

控制系統的誤差預報是指如果控制回路呈現“好”的性能，那么在(k+b)時刻，系統能夠有效克服k時刻進入回路的干擾或者能夠很好地跟蹤設定值的變化，即誤差為零。因為誤差預報值反映的是系統誤差在(k+b)時刻的趨勢，所以它也接近于零。如果控制回路呈現“差”的性能(如振蕩、穩態誤差等)，那么在(k+b)時刻系統誤差則呈現出相應的形式。由于預報值要盡量準確地反映系統誤差在(k+b)時刻的動態行為，因此，它也會表現為其中的某種形式。

對存在干擾的控制系統的輸出，認為是系統對大量連續脈沖的響應。性能“好”的控制回路在一定的預報步長b后系統誤差預報值接近于零，其方差較小;而性能“差”的控制回路，在相同的預報步長b后誤差預報值不能達到零狀態而是表現為相應的形式，其方差就比較大。

2 綜合性能評價方法

在實際工業過程中，擾動信號是許多不同類型的信號的混合體且存在多種操作模式。基于誤差預報的控制系統綜合性能評價方法是針對多操作模式的過程控制系統，提取控制系統可達到的最小方差，通過比較實際誤差序列的方差和預報序列的方差來確定系統的性能指標，實現對控制系統的綜合性能評價。

定義基于誤差預報的控制系統綜合性能指標為:

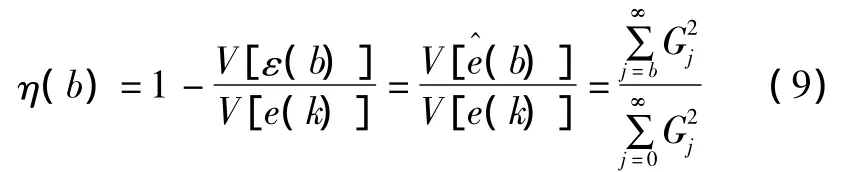
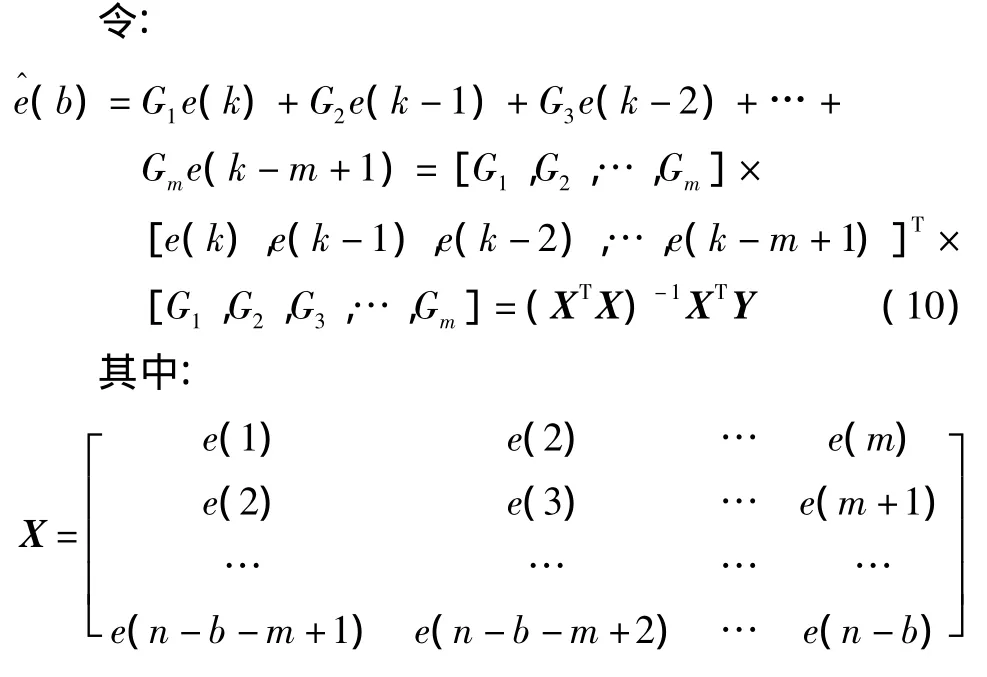
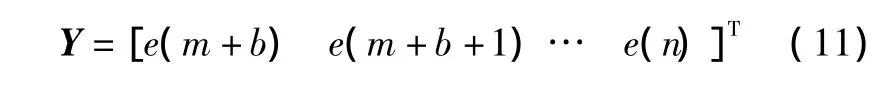
式中:m為模型的階次，同時表示了k時刻及其以前的歷史數據的個數，m太小影響預報的準確性，太大影響運算速度，因此，必須選擇合適的m，以便所使用的歷史數據能夠反映時間序列的特征，一般可選取m為稍大于控制回路的調整時間;b為預報步長，它影響控制系統可達到的最小方差，b太小不能反映系統抑制干擾的能力，太大則不能準確識別系統的性能，一般可以依據經驗公式b=minsη(s)≤0.1選擇;n為時間序列的樣本數，n太小不能完全反映控制回路的特性，而太大則會掩蓋很多重要的信息，同時還會引起很大的計算量，因此，n的選擇既要能夠合理反映回路的特性(尤其是對于設定值改變的過程)，又不能引起太長的運算時間。

3 實例分析

田納西-伊斯曼過程(Tennessee-Eastman process，TEP)仿真平臺是由Eastman化學品公司開發的一個現實工業過程，反應器是其中主要的設備單元之一［10］。TE過程反應器流程圖如圖2所示，氣體原料進入反應器，生成的產品進入下一個流程。該反應是一個不可逆的放熱過程，反應器溫度通過冷卻水回路進行調節。反應器溫度控制系統主要包括溫度控制器TC、冷卻水出口溫度TI和控制閥V1。

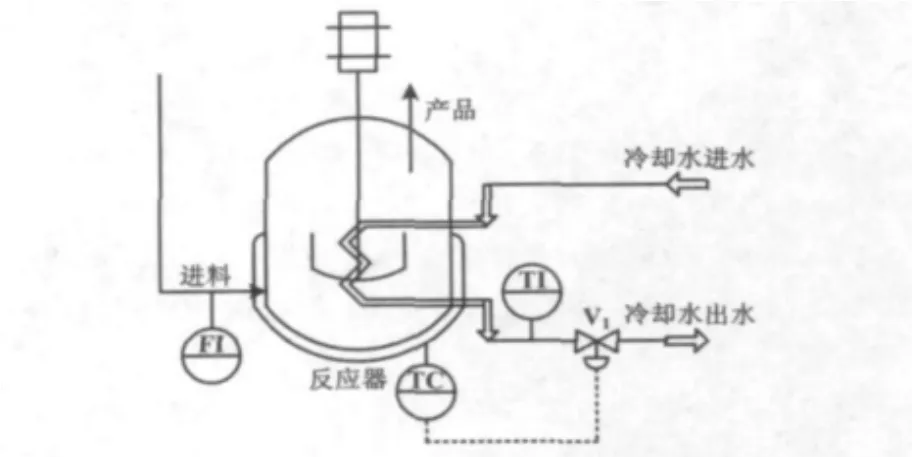
圖2 TE過程反應器流程圖Fig.2 Flowchart of TE process reactor

14組試驗下反應器溫度控制系統的性能指標棒圖如圖3所示。

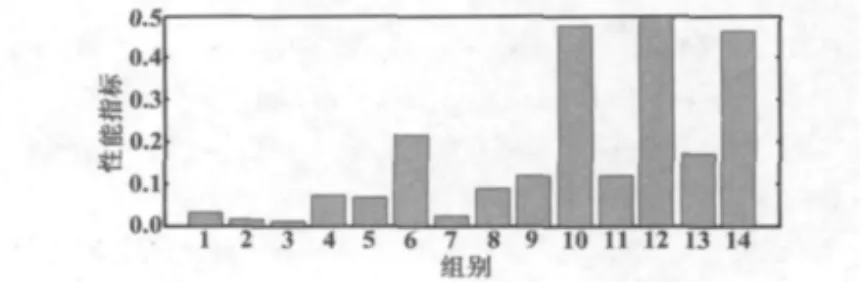
圖3 反應器溫度控制系統性能指標Fig.3 Performance indexes of reactor temperature control system

選擇參數 m=30、n=1000、b=15，針對系統設定值改變的過程、影響系統輸出的階躍干擾過程和控制閥粘滯過程三種情況，對溫度控制系統的綜合性能進行分析，在整個試驗過程中均存在隨機干擾。

由圖3可以看出，第6、10、12、14組的性能指標值很大，表明在這些時間段內控制系統的性能很差，而第13組的性能指標值稍小，說明此時控制系統的性能較差。

結合系統的輸出誤差和誤差預報曲線，對綜合性能評價方法進行具體說明。

3.1 階躍擾動試驗分析

控制系統性能差的一個主要原因是控制器參數設置不合適。當溫度設定值改變時，如果控制器參數設定合適，系統就能夠有效抑制干擾的影響，反應器溫度會很快達到新的穩態值，使得系統性能良好，如圖4(a)所示，這對應于圖3中第2、3組性能指標值很小的情況;而如果控制器參數不合適，反應器溫度要經過很長的時間才能達到新的穩定狀態，使得系統性能很差，誤差及其預報值也會長時間偏離零狀態，從而呈現較大的方差，如圖4(b)所示，這對應圖3的第12組和第14組試驗，其性能評價指標值分別為0.4520和0.4600。在同樣的控制器參數下，單看系統在隨機干擾情況下的性能指標值(圖3的第13組數據η=0.1682)，并不能準確判斷系統性能的優劣。

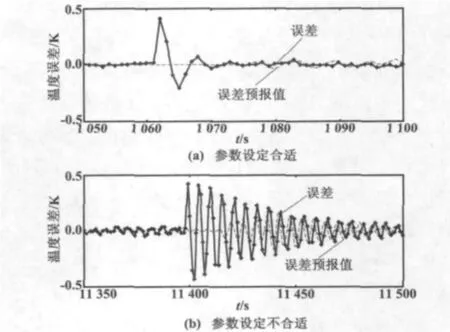
圖4 反應器溫度誤差和誤差預報曲線Fig.4 Reactor temperature error and error predictive curves

當反應器冷卻水入口溫度發生階躍變化時，反應器的溫度會突然升高，這就需要通過閉環控制回路進行調節。與階躍過程的分析類似，當控制器參數合適時，系統性能良好，對應于圖3第4組和第5組試驗，其性能指標η分別為0.0696和0.0644;當控制器參數改變后，控制系統要經過較長的時間達到穩定狀態;而如果控制器參數作進一步改變，系統的性能將會更差，圖3中第4、5、9、10組性能指標反映了這種情況。

3.2 控制閥的粘滯

控制閥的粘滯是工業界常見的引起控制系統性能變差的原因。如圖5所示，在同樣的控制器參數下，圖5(a)中反應器溫度輸出穩定，誤差很小，系統綜合性能良好，對應于圖3的第1個性能指標值;但是第6個性能指標值很大(η=0.2119)，表明控制系統性能較差。分析發現，這是由于該段時間內控制閥性能的惡化使系統性能很差。由于控制閥的粘滯，導致過程輸出和誤差曲線均呈現明顯的振蕩趨勢，誤差預報序列也表現為振蕩形式，方差變大，使得性能指標增大，如圖5(b)所示。

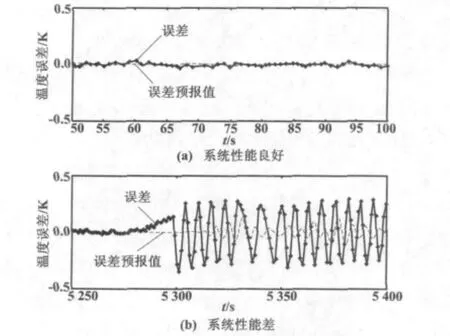
圖5 控制閥粘滯誤差和誤差預報曲線Fig.5 Control valve sticky error and error predictive curves

通過實例分析表明，在工業過程出現擾動和操作模式改變情況下，只采用針對單一模式的控制系統性能評價方式會得出片面的結論，導致錯誤的判斷。基于誤差預報的控制系統綜合性能評價方法能同時針對多種操作模式，利用控制系統可達到的最小方差，對控制系統進行全面分析，從而獲得綜合性能評價指標，使評價結果更加合理，并減少錯誤的判斷。該方法不需要估計擾動模型的特性，彌補了MVC方法的不足，使在線實時評價控制系統的性能成為可能。

4 結束語

本文提出了一種基于誤差預報的控制系統綜合性能評價方法，通過計算系統預報誤差和實際誤差方差的比值得出性能指標，反映控制系統的綜合性能。該指標值可以合理評價控制系統一段時間內的控制效果，使控制工程師能夠實時監測控制系統的性能，從而采取合理有效的措施。實例分析證明了該方法的有效性和實用性。

［1］Jelali M.An overview of control performance assessment technology and industrial applications［J］.Control Engineering Pratice，2006，14(5):441-466.

［2］熊曉菲.過程控制系統性能評價研究與實現［D］.北京:北京化工大學，2007.

［3］Olaleye F，Huang B，Tamayo E.Performance assessment of control loops with time-variant disturbance dynamics［J］.Journal of Process Control，2004，14(8):867-877.

［4］Xu Fangwei，Huang Biao，Tamayo E C.Performance assessment of MIMO control systems with time-variant disturbance dynamics［J］.Computers ＆ Chemical Engineering，2008，32(9):2144-2154.

［5］Ghraizid R A，Mart'inez E，Prada C'esar de，et al.Performance monitoring of industrial controllers based on the predictability of controller behavior［J］.Computers ＆ Chemical Engineering，2007，31(5-6):477-486.

［6］Ingimundarson A，H?gglund T.Closed-loop performance monitoring using loop tuning［J］.Journal of Process Control，2005，15(2):127-133.

［7］Thornhill N F，Huang B，Shah S L.Controller performance assessment in set point tracking and regulatory control［J］.Control Signal Process，2003，17(7-9):709-727.

［8］Thornhill N F，Oettinger M，Fedenczuk P.Refinery-wide control loop performance assessment［J］.Process Control，1999，9(2):109-124.

［9］項靜恬，杜金觀，史久恩.動態數據處理——時間序列分析［M］.北京:氣象出版社，1986:277-280.

［10］蔣浩天.工業系統的故障檢測與診斷［M］.北京:機械工業出版社，2003:98-107.