電磁無心夾具定位面變化對定程磨削尺寸的影響
張果,季軍警
(成都天馬鐵路軸承有限公司 技術一部,成都 610306)
符號說明
D初——定位面的初始尺寸(指調整過程中工件滾道直徑)
D變——磨削過程中滾道直徑
D1正——調整過程中大擋邊外徑
D1變——定位面尺寸為D變時,未磨削外徑尺寸(與D1正相等)
D1實——磨削過程中大擋邊外徑直徑
d正——調整過程中的內徑
d變——定位面尺寸為D變時,未磨削內孔尺寸(與d正相等)
d實——磨削過程中的內徑
f——定位面尺寸變化對磨削面尺寸的影響量(外徑影響量f1,內孔影響量f2)
R砂——砂輪半徑
OJ——初始定位面尺寸工件中心與砂輪中心的距離
OO′——定位面尺寸由D初變為D變時,工件中心在電磁無心夾具上移動的距離
MP——定位面尺寸為D變時,實際定程磨削工件磨削面半徑尺寸距初始對刀工件磨削面半徑尺寸的距離
P點——定位面尺寸為D變時,砂輪和工件表面磨削的切點
α——支承角
β——支承夾角
1 概述
鐵路軸承353130B內圈結構如圖1所示,其大擋邊外徑是裝配油封的油封面,要求與滾道、內徑具有良好的同心度。為消除由于工序定位基準不一致對同心度的誤差影響,工藝順序安排以滾道面做基準支滾道磨滾道,然后以滾道定位對大擋邊外徑和內孔進行加工。磨削方法屬于以外圓定位磨另一外圓、以外圓定位磨內徑面范疇。
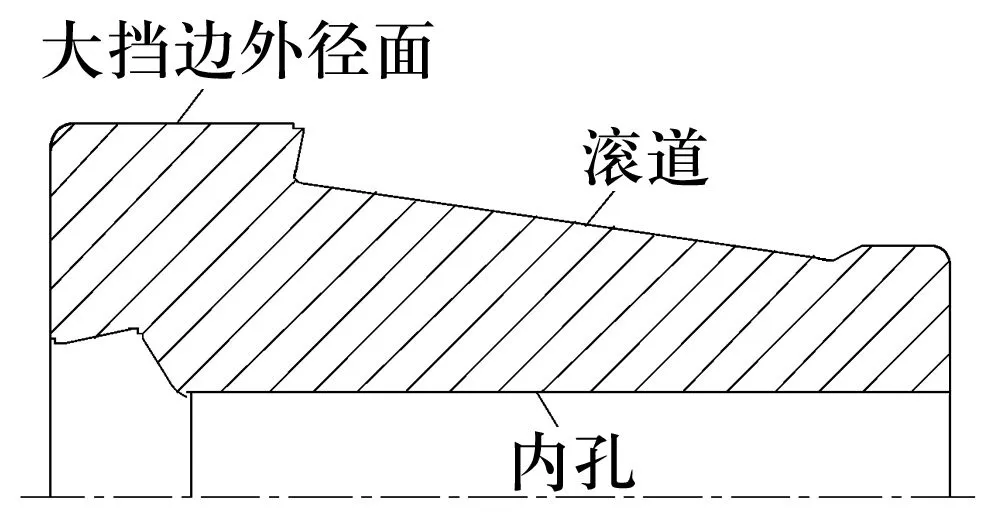
圖1 353130B軸承內圈結構示意圖
套圈磨加工過程中被磨削表面的尺寸精度控制方法主要有:定程法和主動測量法[1]。采用3ME2116半自動機床對工件大擋邊外徑面進行磨削,用MZ2015C半自動機床對工件內徑面進行磨削,尺寸控制方式為定程法。經分析,在機床、砂輪及夾具相關調整參數固定不變時,用定程法磨削外徑和內孔,定位面尺寸有一定公差時,會造成大擋邊外徑和內孔尺寸偏差。
2 電磁無心夾具定程磨工件尺寸變化
電磁無心夾具起徑向定位作用的部件為前、后支承[2]。在定程磨削過程中,設定位面初始尺寸和磨削面的初始尺寸均為技術要求規定的名義尺寸,當定位面由初始尺寸增大或減小到另一尺寸時,磨削面尺寸也將由初始尺寸減小或增大到另一尺寸,磨削面尺寸減小與增大的變化量與支承角、支承夾角、砂輪半徑、定位面尺寸變化量有關。
2.1 滾道定位磨外圓
圖2為以外圓定位磨另一外圓的磨削原理,由圖可知,當定位面直徑由D初變為D變時,工件中心由O點移至O′點,處于第1象限;工件與前、后支承的切點發生變化,兩支承間的定位弦長由BF移至AG,AB和FG分別為工件與前、后支承切點的移動距離;OO′連線的延長線與前、后支承切線相交于N點。由幾何關系可知,砂輪圓周與工件外圓屬于外切,其切點與砂輪中心、工件中心處于同一直線上。由于外圓磨削所用的砂輪直徑較大,接觸弧較短,砂輪半徑對磨削面的尺寸影響較小。
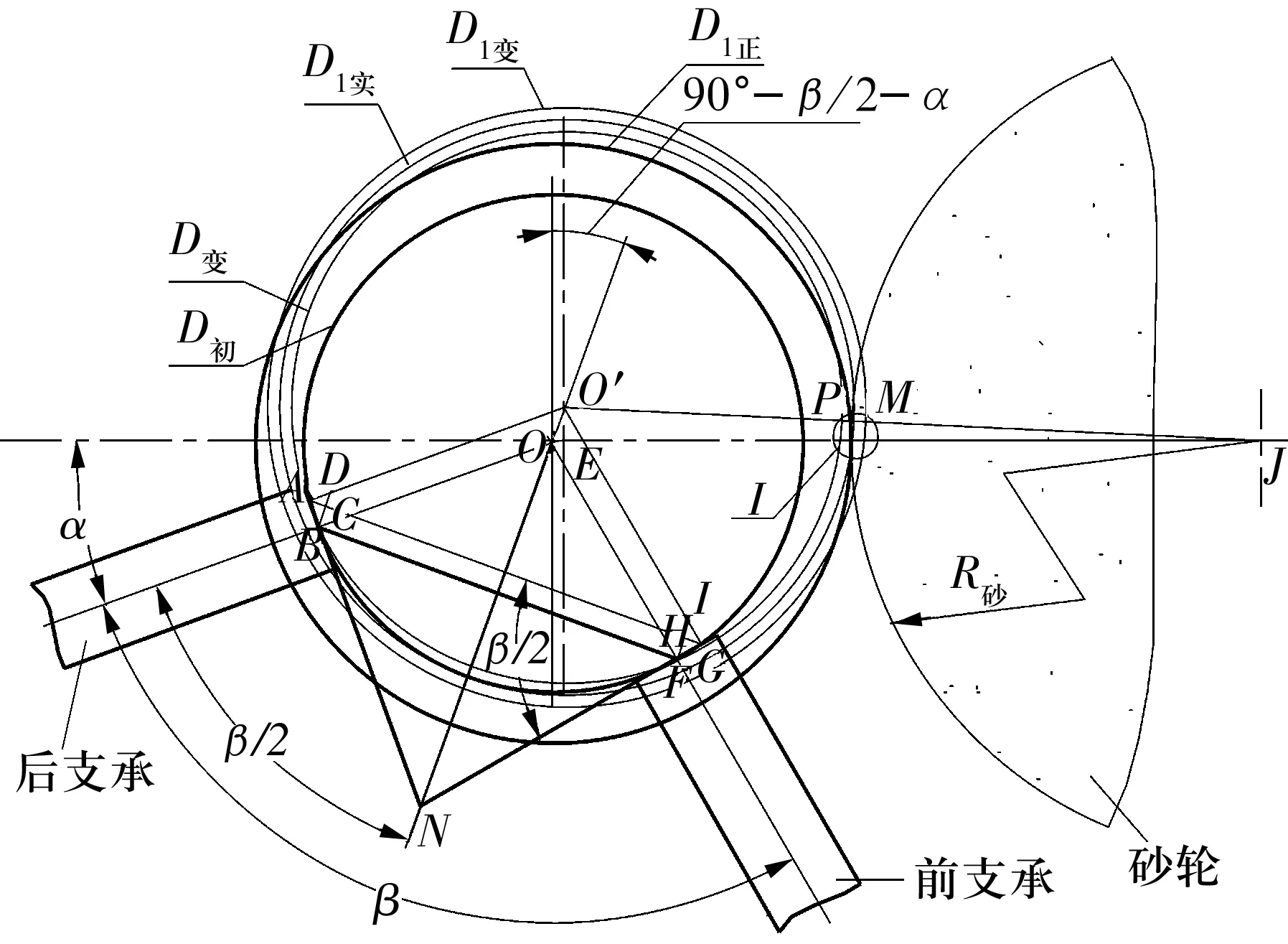
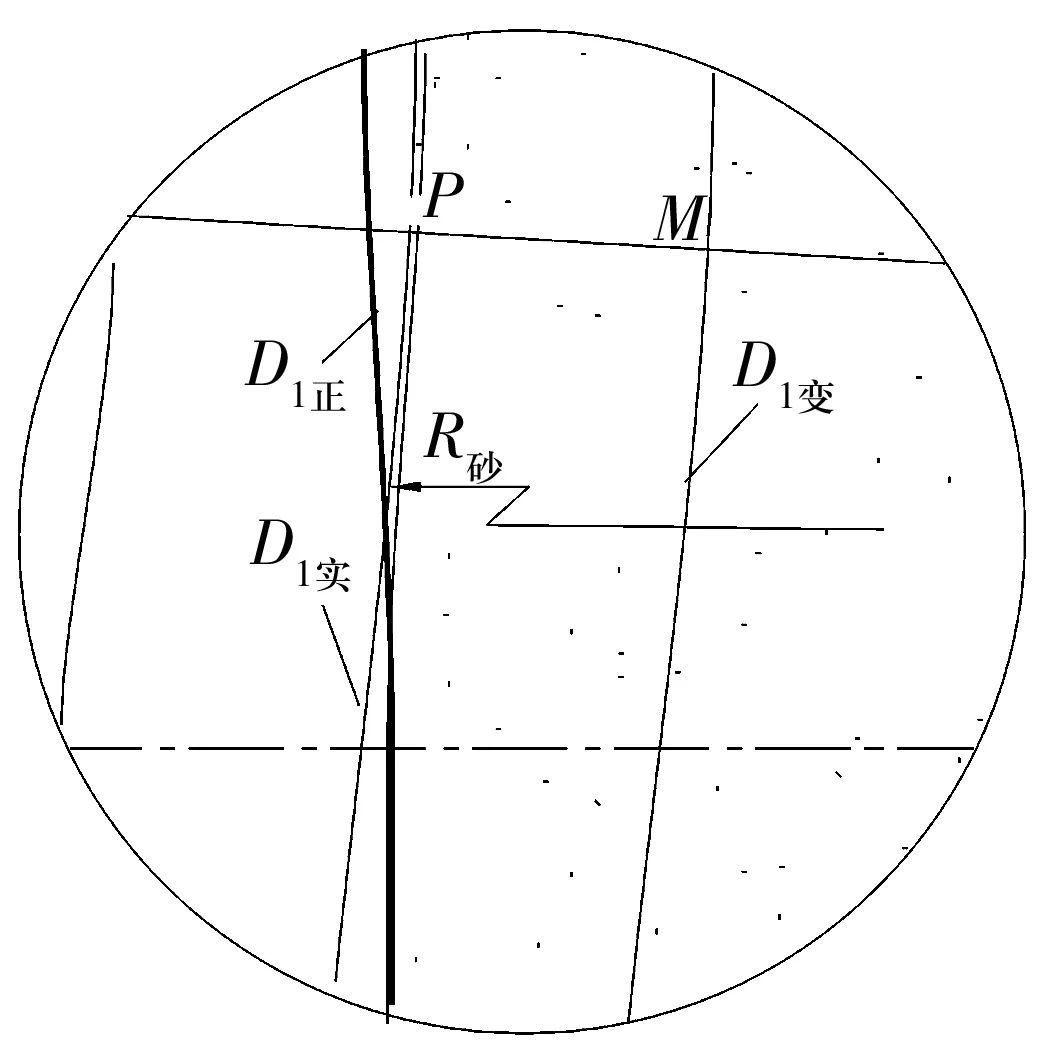
圖2 電磁無心夾具以外圓定位定程磨另一外圓的幾何關系
當定位面直徑由D初變為D變時,對磨削外徑面尺寸影響量為
f1=2MP=2(O′M-O′P)。
(1)
由圖2幾何關系可得:
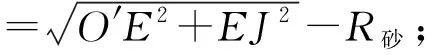

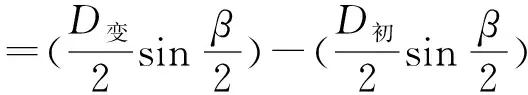
從而得出,磨削外徑面的尺寸偏差量為
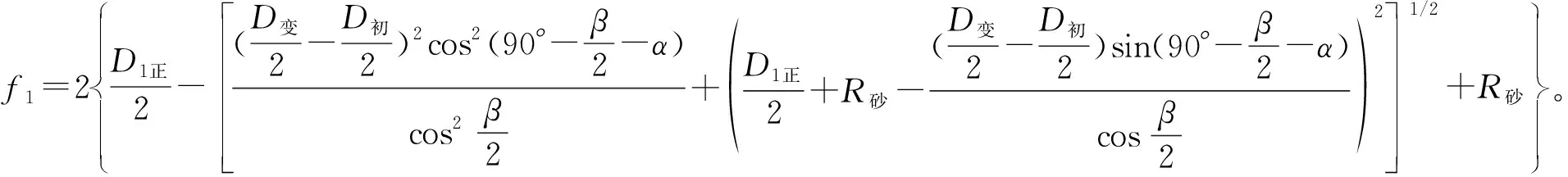
(2)
2.2 滾道定位磨內孔
圖3所示為以外圓定位磨內孔的磨削原理,當定位面直徑由D初變為D變時,工件中心由O點移至O′點,處于第2象限,工件中心與支承、支承夾角的幾何關系與磨外徑面一致。由幾何關系可知,砂輪圓周與工件內徑屬于內切,其切點與砂輪中心、工件中心處于同一直線上。由于內孔磨削所用的砂輪直徑較大,接觸弧較短,砂輪半徑對磨削面的尺寸影響較大。
對磨削內孔面尺寸影響量為
f2=2MP=2(O′P-O′M)。
(3)
由圖3幾何關系可知
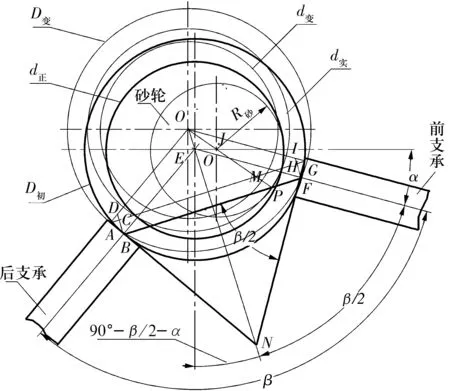
圖3 電磁無心夾具以外圓定位定程磨內孔的幾何關系
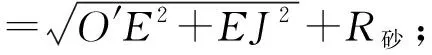
從而得到

(4)
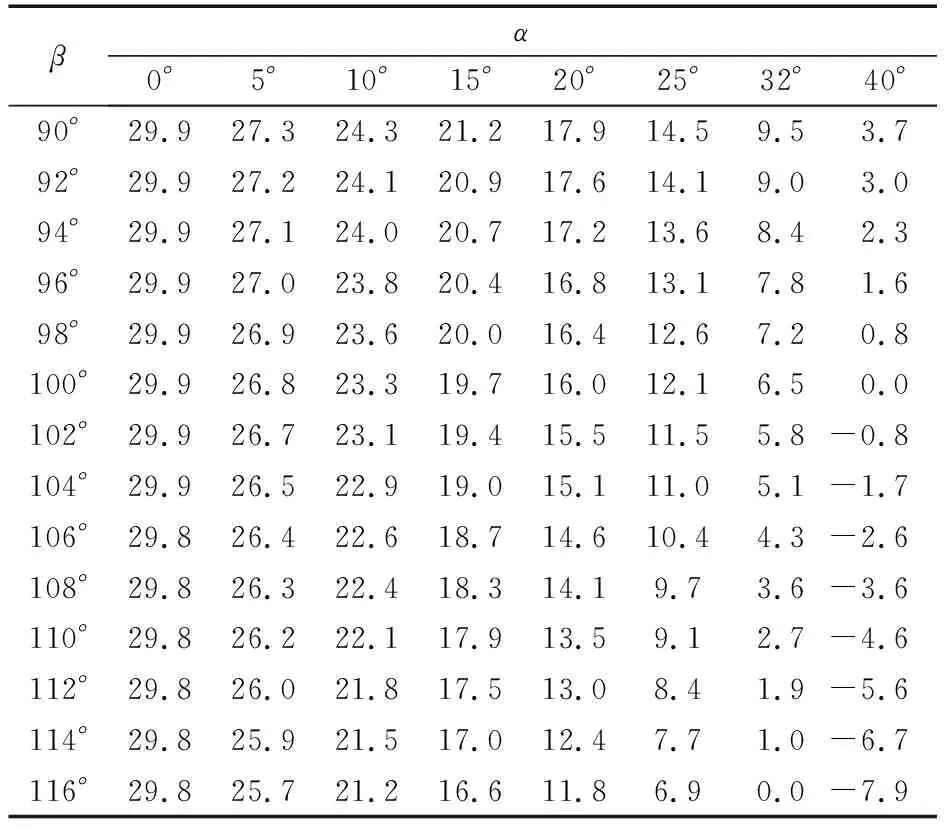
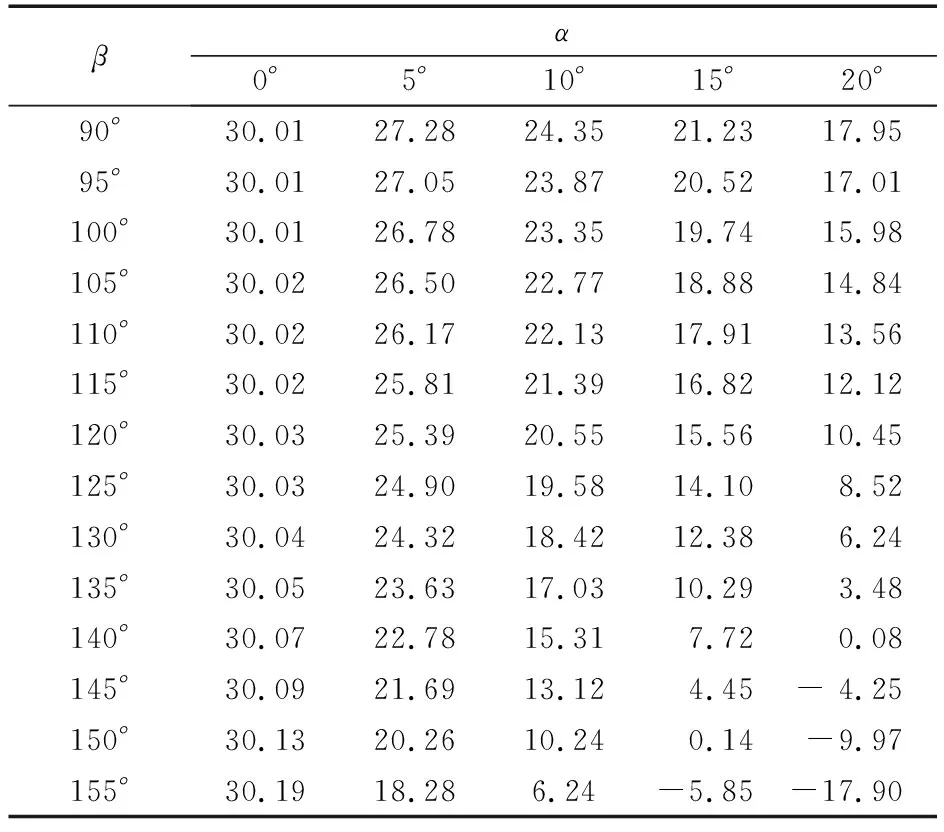
由(2)和(4)式可知,在電磁無心夾具上,用定程法磨削,在初始工件位置調整合格后,以外圓為定位面,磨外徑時尺寸與參數D變,D初,D1正,R砂,α及β有關;磨內孔時與參數D變,D初,R砂,d正,α及β有關。當D變>D初時,f1(f2)的計算結果為正值,表示定位面尺寸欠磨時外徑(內孔)磨削面尺寸的過磨量;當D變 設D初=188.775 mm,D變=188.805 mm,D1正=199.255 mm(公差中間值),d正=149.979 mm(公差中間值)。因砂輪為選型確定,砂輪的尺寸變化在此處不予考慮。由(2)和(4)式可得在砂輪直徑不變、支承夾角不同時,滾道尺寸變化量(已知定位面偏差為0.03 mm)對大擋邊外徑及內孔尺寸變化量的影響值,計算結果見表1、表2。 由表中數據的變化趨勢可知: 表1 定程磨大擋邊外徑面時電磁無心夾具支承角對f1值的影響 μm 表2 定程磨內孔時電磁無心夾具支承角對f2值的影響 μm (1) 當α=0°,β=90°時,定位面欠磨0.03 mm,與大擋邊外徑過磨量0.029 9 mm和內孔面過磨量0.030 01 mm均不等。這是因為定位面欠磨,尺寸變化后的工件相對于初始對砂輪工件的中心移動了一段距離,造成大擋邊外徑與砂輪的外切點由初始位置移至第1象限(若定位面過磨時,則外切點移至第4象限),采用定程磨降低了其影響值;內孔磨削面與砂輪的內切點移至第4象限(若定位面過磨,則內切點移至第1象限),增大了其影響值。 (2) 當α=0°時。定程磨外徑面,尺寸變化后的工件對外徑尺寸的影響量隨著β角的增大而降低;定程磨內孔,對內孔尺寸的影響量隨著β角增大而增大。這是因為在α=0°時,不論定程磨外徑或內孔,β角的增大均能使尺寸變化后工件的磨削面超過砂輪初始位置的距離減小。但內孔磨削前支承處于水平狀態,砂輪與工件的接觸弧很長,反而增大了其影響量。 (3) 定程磨外徑或內孔時,α角越大,β角的增大能降低因定位面尺寸變化造成的大擋邊外徑或內孔尺寸的變化量,且下降速度比α角較小時的下降速度要快。 (4) 當前、后支承調整至α+β/2>90°時,定位面的欠磨(0.03 mm)不會使大擋邊外徑或內孔尺寸過磨,反而會使大擋邊外徑或內孔欠磨。這是因為支承角、支承夾角增大后,定位面變化的工件中心已經處于第2象限(磨外徑)或第1象限(磨內徑)。此條件屬理論計算,在實際生產中為保證電磁無心夾具夾持力、偏心量等,其前、后支承不會調整到此角度值。 結合353130B的工藝調整參數,由上述計算過程可得,當內圈滾道欠磨0.03 mm時,定程磨大擋邊外徑則最大過磨量為0.021 2 mm,最小過磨量為0;定程磨內孔時最大過磨量為0.030 03 mm,最小過磨量為0.000 14 mm。當內圈滾道過磨時,其計算結果均帶負號,絕對值與表1、表2中數據一致,表示大擋邊外徑或內孔尺寸的欠磨量。 進一步計算發現,當α為負值時,β的增加將會增大定程磨大擋邊外徑或內孔尺寸的影響量,α的絕對值越大,則β的增加將會越快地增大定程磨大擋邊外徑或內孔尺寸的影響量。這與α為正值的情況相反,因為α為負值時,定位時會將工件大擋邊外徑或內孔向砂輪中心方向推動的距離增大,因此,在生產調整中要避免α角為負值的情況。 對f1(f2)的影響不僅與α和β有關,而且還與D變,D初,D1正(d正),R砂有關。在α和β角保持不變的情況下,D變,D初,D1正(d正),R砂對f1(f2)的影響如下: (1)D變與D初的值相差越大,工件定位面尺寸穩定性越差,其對定程磨削外徑面或內孔面的影響量越大。 (2)D1正和d正對f1和f2的影響由(2)式和(4)式可知:當D1正增大或減小時,f1隨之增大或減小;當d正增大或減小時,f2隨之減小或增大,但D1正和d正對f1和f2值的影響非常的小。因為D1正(d正)的變化僅表示工件與砂輪切點的變化,對f1(f2)的影響可忽略不計。 (3)磨大擋邊外徑面時,砂輪直徑大,工件與砂輪的接觸弧很短,砂輪半徑對定程磨外徑面的影響較小。磨內孔時,砂輪直徑小,工件與砂輪的接觸弧較長,砂輪半徑對定程磨內孔的影響較大,砂輪半徑的影響趨勢為砂輪半徑增大,影響量增大;砂輪半徑減小,影響量隨之減小。 根據上述分析,為降低因定位面尺寸不穩定對磨削面精度帶來的影響,在生產調整過程中,可采取以下措施來減小定程磨f1(f2)值: (1) 在產品形狀、位置公差合格的情況下,應增大α和β,并避免α+β/2>90°。 (2) 采取工藝方法,在磨削定位面時壓縮其公差帶,減小定位面的不穩定值,以保證定位面的精度要求。 (3) 當以外徑面定位對內孔進行定程磨削時,在保證砂輪足夠切削力、切削速度的情況下,應盡量減小砂輪直徑。 (4) 在磨削加工中,能采用主動測量方法時應避免用定程法進行尺寸控制。 (1) 定程法磨削外徑面(內孔)時,定位面欠磨會導致外徑面(內孔)過磨;定位面過磨會導致外徑面(內孔)欠磨。 (2)α和β增大,能減小定位面欠磨或過磨時對外徑面和內孔尺寸的影響,減小量受α和β增大量的控制。 (3) 當α+β/2>90°時,定位面的欠磨不會造成外徑面和內孔面的過磨,反而使外徑面和內孔面欠磨;定位面過磨也不會造成外徑面和內孔面的欠磨,而會使外徑面和內孔面過磨。因為工件中心所處的象限在α+β/2>90°時發生變化。 (4) 以外圓定位定程磨外圓時,砂輪半徑對f1值的影響很小,可忽略不計。以外圓定位定程磨內孔時,砂輪半徑對f2值的影響較大,必須予以考慮。 (5) 定程磨削中,初始對砂輪尺寸D1正(d正)是調整時必須得到的具體值,以便運用公式進行計算,為調整機床提供有益參考。 (6) 作為基準面的磨削定位面的尺寸公差應盡量小,以避免其散差較大而對磨削面造成過大的偏差。3 電磁無心夾具參數對f的影響
3.1 支承夾角
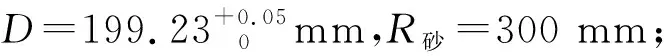
3.2 其他參數的影響
3.3 優化措施
4 結論

