An Estimation Method for Kill Probability Based on Random Residence Time Series

LIU Chao(劉超)，WANG Jun(王軍)，GUO Zhi(郭治)

(1.School of Mechanics，Jiuzheng University，Jinzhong 030600，Shanxi，China;2.School of Automation，Nanjing University of Science and Technology，Nanjing 210094，Jiangsu，China)

Introduction

In order to make weapon systems have as far as possible higher shooting efficiency for the maneuver target within a valid shooting area，a suitable shooting system must be established for different kinds of shooting process［1］.For tank systems，the shooting area is the projection of their shot door to the target's head-on bullet;for antiaircraft guns，the shooting area is the coming airspace window;for trace aiming systems，the shooting area is the current airspace window.In fact，the flight path of maneuver target can be divided into a constant component and a random component.So far，more researches focus on the prediction of constant component.However，in many published literatures，the random component usually is treated as random disturbance which not be brought into the performance index.If the prediction of constant component of target is more accurate，which enable the center of shooting area hold relative identity with the flight path，the random component of target will smoothly random pass through the shooting area in the sense of stationary random process.The Ref.［2 －3］studied the probability modeling and its accuracy when the maneuver target randomly passes across shooting area.Based on these models，the Ref.［4 －5］further studied the estimation of kill probability within passing period and residence time respectively.The Ref.［6］studied the kill probability estimation in given number of random crossing processes.All these studies are based on the conception，that is，the shooting action starts only when the target is in shooting area and stay in the area at the moment of the bullet arrived，the shot may hit the target as probability.

In fact，the setting of shooting area，determining of bullet's scattering and the density，shooting rate and bullet speed，and the target's maneuver ability，all jointly determine the resident time of target and the hit probability of weapon.Since the random property of resident time，even at the suitable disposition in above conditions there may appear the some short sections of resident time that is less than the respond time of firing bullet，then this shooting can not hit target in those short resident times.Even though the target might randomly cross the shooting area many times during the bullets fly to the shot area，the probability for bullet and target appearing in shot area at the same time is very small.Therefore，it is significant in practice to investigate the kill probability in those large resident times which greater than firing respond time.The common kill probability is defined as a probability of hit predetermined bullets under the condition of given total ofshooting bullets orgiven continually shooting time［7－8］.However，because the target's resident time in shooting area is stochastically variable，in the analyses of shot efficiency and kill proportion under maneuver，the probability properties of resident time series must be brought into our discuss.In this paper，the estimation approach of hit or kill probability in given time interval in the target random crossing the shooting area，based on the probability relationship between the given time and resident time series，as well as the properties of shooting delay of weapon system，is studied.A method to evaluate the probability of the number of effective resident times greater than a known value in given time interval is proposed.The expressions and their approximate formulas are derived，and some discusses and conclusions are given also.

1 Descriptions and Theorems

Definition 1A shot process during a target stays in the shooting area is called an effective shot or resident shot.

Definition 2The probability that hits come up to or more than specified number，according to determined shooting law in given time，is called randomcrossing kill probability.

If the distributions of resident time and waiting time are Poisson distribution with the parametersμ0andμ1，respectively，then，in a given timetg，the mean number of resident times in the given time is［9］

It can be seen that，if giventg，then the mean numberof resident time intgcan be determined.Therefore，takingasa statisticalamountand analyzing the statistical amount of resident times intg，some other relative statistical amounts can be obtained.Thus，the Definition 2 can be further described as follows.

Definition 3The probability that hits come up to or more than specified number，according to determined shooting law in given a mean number of resident time，is called random-crossing kill probability of given resident time series.

Considered there exists a system delay timetd，between the weapon system's firing command to the bullet leaving out，the practical effective resident time for shooting target，denoted aste，shall satisfyte≥td.In this case，there exits hit probability in the resident time series{X1，X2，…，XN}which numbers determined by，and those values of resident time meet with no less thantd.

Underξ=tinit，{N(t－tinit)，t≥tinit}is a counting process of the random shooting.Denoteξ≥0 as the moment of target entering shot area，t≥ξas the moment of leaving shot area.So that，ξandtare all positive stochastic process，and then the counting process is a conditional counting process of resident time and denoted as{Nξ=tinit(t－tinit)，t≥tinit}.

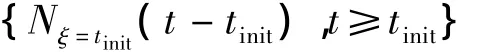
Lemma 1Suppose that a counting process{Nc(t)，t≥0}is Poisson process withγ.If the occurrence probability of a class of events isp，while the occurrence probability of another class of events is(1－p)，then{Nc(t)，t≥0}can be split up into two Poisson distributions{Nc1(t)，t≥0}and{Nc2(t)，t≥0}with parameterspγandγ(1 －p)，respectively.

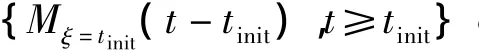
Proof 1From the given condition，it can be known that，in the resident shot，the shot numbersNξ=tinit(t－tinit)is a Poisson process withγ.Therefore，the number of resident hits can be expressed as

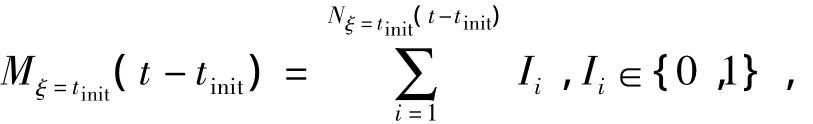
whereIiis the property function of thei-th shot，that is，it is 1 when target is hit;otherwise，it is equal to 0.In fact，Iiis a(0 －1)distribution

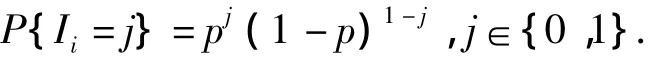
From Lemma 1，we can conclude that{Mξ=tinit(ttinit)，t≥tinit}is a Poisson process with parameterpγ，that is，the probability ofkhits in a resident shot is

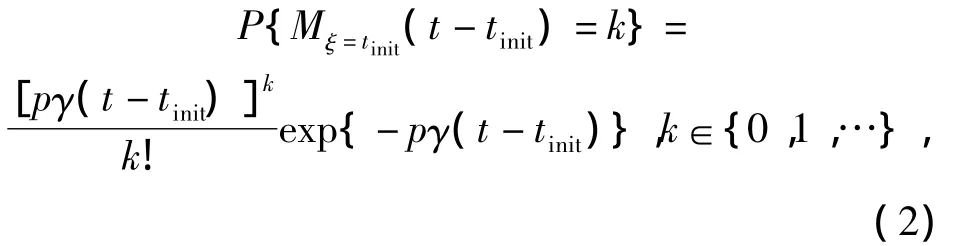
where(t－tinit)is the resident time which is a random variable，can be denoted astr=(t－tinit).Thus，Eq.(2)is a stochastic function with the parameterkand the random variabletr.Further，the Eq.(2)can be expressed as

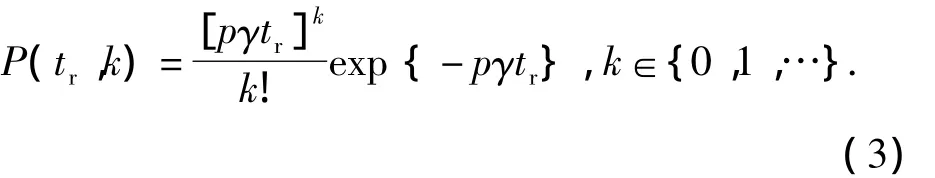
Theorem 2In a resident time，the inferior limit of the resident time，for more thankhits，shall satisfy

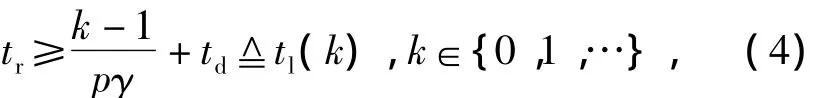
wheretdis the weapon's shot delay from the shot command at the momentum of target entering shooting area to the bullet leaving out.

Proof 2If the shot time interval is exponential distribution withγ，then the average of shot interval equals to 1/γ.From Theorem 1，it can be known that the average time interval of hits is 1/(pγ)，then the need lowest average resident time forkhits is(k－1)/(pγ).Considered the first shooting delay timetd，then the needed resident timetrfor more thankhits shall be greater than the inferior limitt1(k)，as a result，Eq.(4)must be satisfied.

The Eq.(4)gives the relationship between thekhits and the minimum mean of effective resident time.Therefore，the kill probability can be estimated by solving the number of effective resident time inrelated to a given timetg.In what follows，we will derive the probability of the number of resident time that is greater than the effective resident time inin giventgbased on a property of Gamma distribution，known that the resident time is a exponential distribution.

Lemma 2［10］If{Yi，i=1，2，…}are mutually independent and identical distribution，which is the Gamma distributionΓ(n，b)with the parametersnandb，then the probability function ofYiis

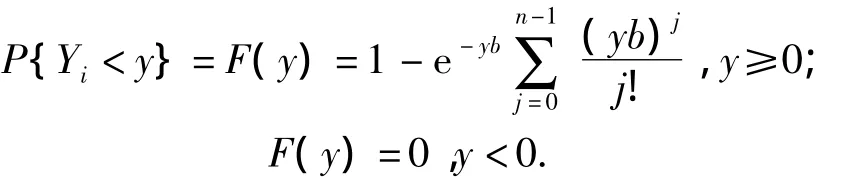
Theorem 3If the random seriesX={Xi，i=1，…}are mutually independent and identical distribution following Gamma distributionΓ(n，b)withnandb，given a positive constantCwhich can betl(k)in Eq.(4)or another arbitrary constant，letL=，Ti∈{0，1}，where

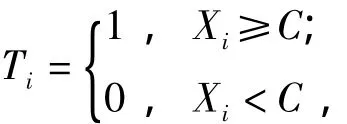
then，inX，the probability of the numberlthat no less than givenCis

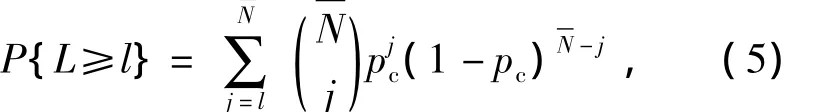
where

is the probability ofXi≥C.

Proof 3From the independency of the series{Xi，i=1，…}，it can be seen thatLis a Binomial distribution with parametersandpc，thus，Eq.(5)holds.Also，from Lemma 2，we have

Theorem 4If the resident time series are mutu-ally independent and identical exponential distributionEP(b)withb，then the probability of numberlof effective resident times inis

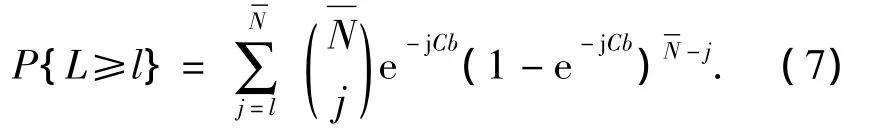
Letn=1 in Eq.(6)，and substitute it into Eq.(5)，then Eq.(7)can be obtained.

2 Kill Probability of Resident Time

2.1 Expressions of Kill Probability

Suppose the scattered bias density function of bullets in shooting area isfand the shot action starts at the moment of target's head-onΩ0falling into the shooting area.Then，the total mean probability of single hit in two-dimensional shooting field is

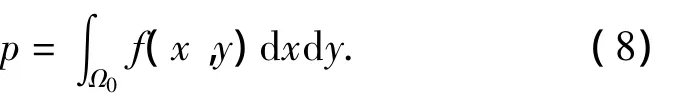
1)Kill probability for given resident time series

Withintg，the probable range of resident timetris 0≤tr≤tg，but for those meetingtr≤td，the hit probability is almost zero.If the kill of a target needs at leastmhits，from Eq.(4)，trshall satisfy the inequalitiestl(k)≤tr≤tg，lk≥m，1≤k≤m，wherelis the number of effective resident times that satisfytr≥tl(k)within.DenoteP{m|}as the hit probability ofmhits withinresident time series.Then，from Theorem 3 and 4，when given the parametersμ0，，mandk，the kill probability at leastmhits in resident time series can be expressed as

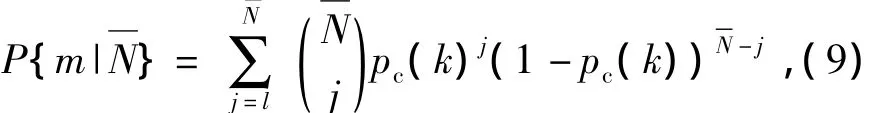
2)Kill probability within first resident time

Takingk=min Eq.(4)，andl=1，=1 in Eq.(9)，the kill probability of greater than or equal tomhits，within the first resident time，can be written as

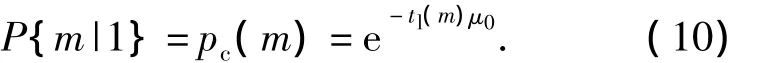
2.2 Approximate Evaluation for Kill Probability

Usually，it is inconvenient to calculate the kill probability by using Eq.(9).Thus，we will give two approximate formulas.

1)If，mandm－are all relatively great，from Stirling approximate formula，Eq.(9)can be approximated as

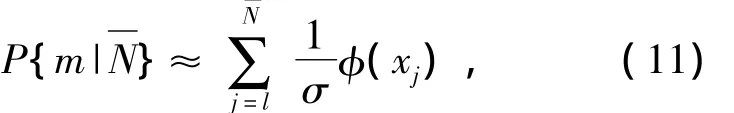
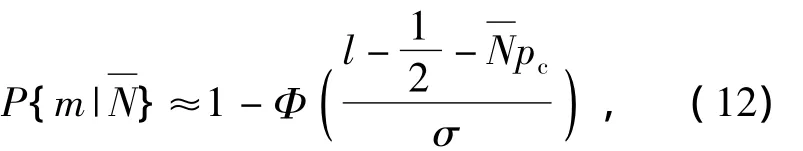
where，Φ(·)is a standard normal distribution function.

2)Ifis very large，butpcvery small，usually，≥10，pc≤0.1，from Poisson formula，the Eq.(9)can be simplified as

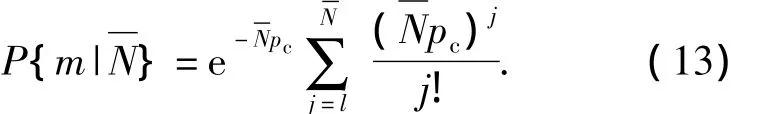
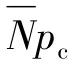
3 Application and Simulation Analyses

In fact，μ0andμ1are fixed for a given shot area or a specified maneuver target.Thus，in the given timetg，we can obtain the mean numberof resident times from Eq.(1).From the least number ofmhits needed to kill target，the scatter density of bullets and disposition of weapons shall be reasonably set up inresident times in order to ensure that there are more thanmhits among the shot bullets in.The mean of shooting interval 1/γcan be determined by using the shooting scatter density.

The main results obtained from Eq.(9)and Eq.(12)will be tested and analyzed by using simulations.In order to simplify calculations and compare conveniently，the simulation results are given by several dimensionless parameters under given.Let=10，p=0.08，γ=30 andtd=0.6，the mean resident times are taken as 1/μ0=0.6，1，1.5，2，2.5，respectively.The expected hit times are set asm=1，2，3，4，5 respectively andl=1.The kill probability of at leastmhits，in the giventgand at least one resident time amongis estimated.

From given parameters above，we can obtain the kill probability of hitting at leastmhits in the giventgfrom Eq.(9)or Eq.(12).

Some simulation results are listed in Tab.1.The value 0.827 90 in the table's first column and row shows that the kill probability for at least one bullet is hit in giventgunder knownμ0andμ1，similarly，the value 0.545 98 in second column shows the kill probability for at least two bullets under same conditions，and so on.

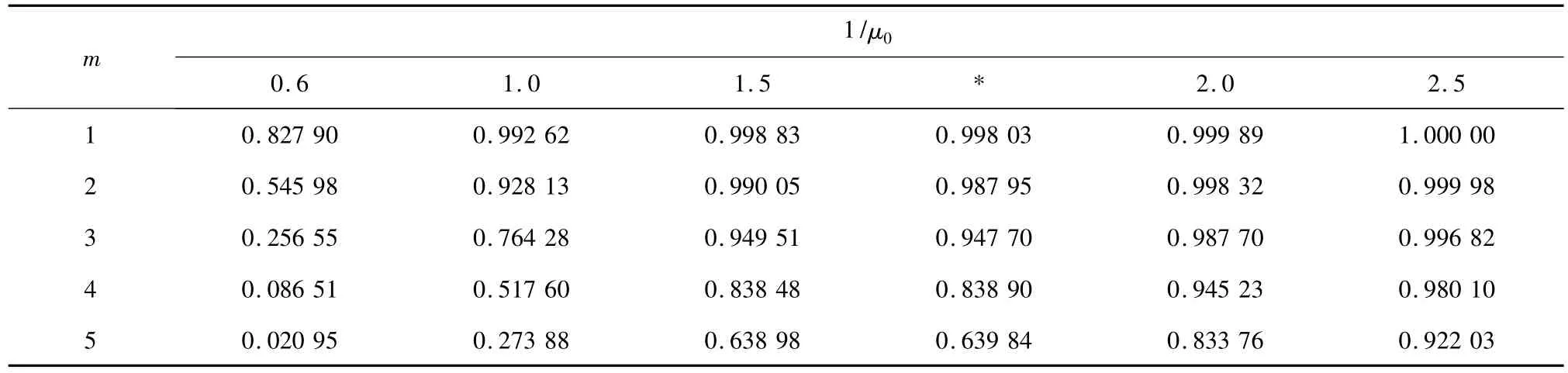
Tab.1 Analysis results on kill probability of residence time series(N=10)

From this table，it can be known that，ifmis fixed，then the kill probability will increase with 1/μ0increasing.It means that，when the mean resident time increases，the number probability of effective resident time needed for killing target will also increase，thus，the hit probability of anticipated at leastmhits increases also.Therefore，we can draw a conclusion that，when 1/μ0becomes very large，the resident kill probability will tend to the common situation that the time of shooting is unlimited.Thus，the kill probability problem under common condition only is one special case belong to the situation discussed in this paper.When the resident time parameters are fixed，the kill probability will decrease withmincreasing.It means that，when the mean resident time is unchanged，the number of effective resident times which satisfy a large anticipated hit numbermwill decrease;therefore the kill probability inevitably decreases along withmincreasing.The data in the table's column marked with asterisk‘*'are evaluated by using the Eq.(12)under the parameter 1.5 that correspond to the ahead column.Obviously，a more accurate evaluation can be obtained by using Eq.(12)in the similar circumstances.

From Eq.(9)，it can be seen that the appeared probability of anticipated hit numbermwill be different under different givenl，and the probabilities have the same chance to appear for eachl.Thus，iftgandmare given，there are maximum and minimum probabilities for at leastmhits.That is，there is a probability interval

The mean of above probability interval can be expressed as

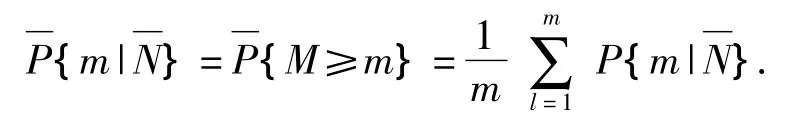
The above equation shows the mean of all the possibly appeared kill probability for at leastmhits in giventg.Therefore，using this way，we can analyze the kill probability of a weapon system for a class of maneuver target as a whole.

4 Conclusions

In this paper，we firstly discuss the relative characteristics of the hit probability and kill probability through statistical resident time series in given time based on the relationship between fixed time and resident time，and obtain the relation expressions of effective resident time to hit numbers.Then，using some properties of Poisson process and Gamma distribution，the mathematical expressions and approximate formulas to estimate the kill probability in fixed time through calculating the probability of the number of effective resident time in the mean resident time series are derived.Finally，a practical application is given out，and the relations of kill probability with parameters and the results effectiveness are analyzed by applying simulations.All the results show that the kill probability under the commonly shooting situation can be classified a special case that belongs to the situation discussed in this paper，so this method has more universality and can offer a practical way to evaluate the kill probability under the maneuver conditions.

［1］GUO Zhi.Modern firepower control theory［M］.Beijing:National Defense Industry Press，1996.(in Chinese)

［2］LIU Chao，GUO Zhi，WANG Yuan-gang.Residence property and probability estimation［C］∥Beijing Proceedings of the First International Symposium on Test Automation and Instrumentation，2006:510－ 514.(in Chinese)

［3］LIU Chao，GUO Zhi，WANG Yuan-gang.Estimate of probability models on maneuver object crossing shot door［J］.Journal of System Simulation，2008，20(3):679 －701.(in Chinese)

［4］LIU Chao，WANG Yuan-gang，GUO Zhi.The period hits probability of random target passage shot area［J］.Acta Armamentarii，2008，29(5):518－584.(in Chinese)

［5］LIU Chao，GUO Zhi.Kill probability and its statistical probability in a residence time［J］.Fire Control and Command Control，2008，33(6):34 －38.(in Chinese)

［6］LIU Chao，GUO Zhi.Kill probability and its statistical property for residence time series［J］.Journal of North University of China，2008，29(1):32 －37.(in Chinese)

［7］XU Pei-de，YU Bin，MA Man-hao，et al.Basic of military operations research［M］.Changsha:National Defense Scientific University Press，2007:113 － 115.(in Chinese)

［8］SUN Hua-sheng，WANG Yong-liang，LV Peng，et al.An analysis of efficiency for single tank's firing based on statistical experiment method［J］.Fire Control and Command Control，2007，32(2):101 －103.(in Chinese)

［9］LIU Chao.The analysis on random-across model and firing efficiency in fire control［D］.Nanjing:Nanjing University of Science and Technology，2009.(in Chinese)

［10］Stone C J.A course in probability and statistics［M］.Califarnia:Wadsworth Publishing Company，1998:136 －139，182 －183.